Системы с восстанавливаемыми элементами

Для систем с восстанавливаемыми элементами из (9.3) и (9.4) вытекают следующие формулы для расчета коэффициентов готовности и простоя:

Коэффициенты готовности и простоя

(9.10)

Если распределения наработки между отказами элементов – показательные с параметрами λ_i, это же справедливо и для системы, а для значений ее параметра и средней наработки на отказ существуют еще формулы, аналогичные (9.7) и (9.9):

и (9.11)

Среднее время восстановления

Среднее время восстановления системы может быть выражено через значения её коэффициента готовности К_г и средней наработки на отказ Т_о : Т_в = Т_о(К_г^-1 – 1). Выражая К_г и Т_о, по формулам (9.10) и (9.11) и подставляя К_{г i} = (1 + λ_iТ_{в i} )^-1, получим, что Т_в может быть представлено в виде:

Последнее приближение справедливо при условии T_{в I} << T_{о i}, оно пренебрегает возможностью совпадения периодов неработоспособности разных элементов.

10. Параллельные системы, расчет их надежности

Параллельной называется система, которая работоспособна тогда и только тогда, когда хотя бы один элемент в ней работоспособен.

И в этом случае параллельное соединение в смысле надежности следует отличать от физического (электрического) соединения. Так, последовательное соединение резисторов является параллельным соединением в смысле надежности по отношению к отказам типа «короткое замыкание» (если сопротивление цепочки меняется в допустимых пределах)

Структурная функция

ф(x)=\/ x_i = max x_i = 1 – П (1-x_i) = 1 – П x_i’ (x_i’ = 1-x_i) (10.1)

Вероятность работоспособности системы

P = 1 – П q_i = 1 – П (1-p_i) (10.2)

Наработка до отказа параллельной системы с невосстанавливаемыми элементами

ξ = max { ξ_i }; i = 1,…,n.

Если все элементы имеют показательное распределение наработки до отказа, то

Интегрируя это выражение по t от 0 до ∞, получим среднюю наработку системы до отказа:

В случае равнонадежных элементов со средней наработкой до отказа Т_е = 1/λ_i

T = (1 + ½+ … + 1/n) T_e

11. Последовательные и параллельные системы с зависимыми (положительно коррелированными) элементами.

Ковариация и коэффициент корреляции

Сделанное выше предположение о независимости состояний элементов системы не всегда выполняется на практике. В теории вероятности в качестве меры зависимости двух случайных величин вводится их ковариация, определяемая следующим образом:

cov(X,Y) = M { (X-MX)(Y-MY) }. (11.1)

Через неё выражается часто используемый коэффициент корреляции

ρ(X,Y) = cov(X,Y) / (DX*DY), (11.2)

представляющий собой, по существу, нормированную ковариацию, поскольку |ρ(X,Y)| ≤ 1.

Поскольку дисперсии с.в. X и Y положительны, знаки ковариации и коэффициента корреляции всегда совпадают.

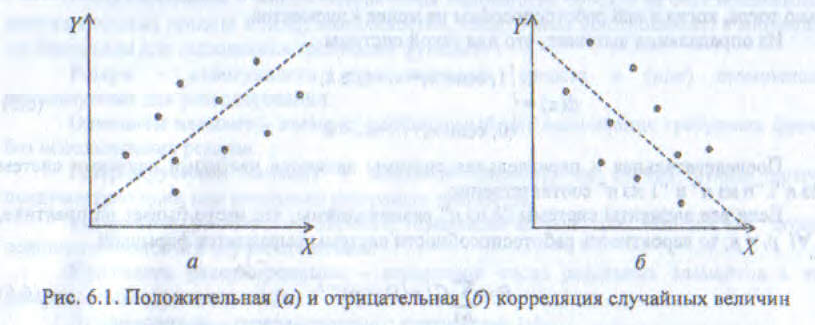
Для независимых случайных величин ρ(X,Y) = 0. Когда ρ(X,Y) > (<) 0, случайные величины называют положительно (отрицательно) коррелированными. Характер поведения таких величин показан на рисунке 6.1. Если ρ(X,Y) ≥ 0 случайные величины называют неотрицательно коррелированными или связанными.

Из определения ковариации (11.1) вытекает, что

M(XY)= M X* M Y+cov(X,Y) (11.3)

Откуда видно, что для связанных случайных величин M(XY) ≥ M X* M Y. Можно показать, что это справедливо и для нескольких множителей.

На практике состояния некоторых элементов системы часто бывают положительно коррелированными. Это обусловлено тем, что они подвержены действию одних и тех же факторов внешней среды (температуры, влажности, давления, вибрации и т.д.), обслуживаются тем же персоналом и т.п. Кроме того, отказ какого-то одного элемента может вызвать увеличение нагрузки на другие элементы, что ведет к возрастанию вероятности их отказов. Поэтому в подобных ситуациях ρ(X,Y) ≥ 0.