
- •1. Матрицы и действия над ними.
- •2. 1 2 3 И n порядок
- •3. Свойства определителей.
- •4. Разложение определителя по строке или столбцу.
- •5. Определитель произведения матриц.
- •6. Формулы Крамера для решения системы линейных уравнений.
- •7. Обратная матрица и ее вычисление.
- •Свойства обратной матрицы
- •8. Свойства обратной матрицы и новый вывод формул Крамера.
- •9. Определение n-мерных арифметических векторов и действий над ними.
- •10. Линейная зависимость и независимость векторов.
- •11. Максимальная линейно независимая подсистема векторов. Линейная зависимость векторов
- •Свойства систем векторов
- •12. Определение ранга матрицы. Теорема о ранге матрицы.
- •13. Теорема о равенстве числа векторов в двух максимальных линейно независимых подсистемах векторов.
- •14. Вычисление ранга матрицы методом окаймляющих миноров. Метод окаймляющих миноров
- •15. Вычисление ранга матрицы методом элементарных преобразований.
- •II. Метод элементарных преобразований
- •16. Теорема Кронекера-Капелли. Решение систем на основе теоремы Кронекера-Капелли.
- •17. Однородная система линейных уравнений. Свойства ее решений.
- •18. Фундаментальная система решений однородной системы линейных уравнений и теорема о числе решений в ее составе.
- •19. Связь решений линейной неоднородной и соответствующей ей однородной систем.
- •20. Метод Гаусса решения линейных уравнений.
- •§ 3. Декартова система координат в пространстве
- •§ 1. Декартова система координат на плоскости
- •22. Полярные координаты на плоскости и их связь с декартовыми прямоугольными координатами.
- •§ 2. Полярная система координат на плоскости
- •23. Понятие свободного вектора. Теорема о проекции вектора на ось.
- •Свободный вектор
- •24. Координаты вектора и их вычисление по координатам его начала и конца. Направляющие косинусы.
- •25. Длина вектора и формула для вычисления расстояния между двумя точками пространства.
- •1.6. Расстояние между двумя точками
- •26. Линейные операции над векторами. Линейные операции над векторами
- •27. Основные теоремы о проекциях векторов.
- •28. Разложение векторов на компоненты.
- •29. Скалярное произведение векторов и его свойства.
- •Геометрический смысл скалярного произведения векторов
- •Алгебраические свойства скалярного произведения
- •Геометрические свойства скалярного произведения
- •30. Векторное произведение векторов и его свойства.
- •Алгебраические свойства векторного произведения
- •Геометрические свойства векторного произведения
- •Выражение векторного произведения через координаты векторов
- •31. Смешанное произведение векторов и его свойства.
- •1.16. Смешанное произведение векторов и его свойства
- •Геометрические свойства смешанного произведения
- •Алгебраические свойства смешанного произведения
- •32. Общее уравнение прямой на плоскости.
- •33. Уравнение прямой в отрезках.
- •34. Нормальное уравнение прямой. Вычисление расстояния от точки до прямой на плоскости. Общее уравнение прямой
- •35. Общее уравнение плоскости.
- •36. Уравнение плоскости в отрезках.
- •37. Нормальное уравнение плоскости, Расстояние от точки до плоскости.
- •38. Канонические уравнения прямой.
- •39. Эллипс: уравнение, общий вид и свойства кривой.
1. Матрицы и действия над ними.
Рассмотрим матрицу вида:

Можно пользоваться сокращенной формой записи:
A = ( aij ); i = 1, 2, 3, .... , m ; j = 1, 2, 3, ....., n .
О. Нулевой матрицей называется матрица все элементы которой равны 0.
О. Две матрицы одинаковой размерности mxn называются равными, если на пересечении i-й строки и j-го столбца в одной и в другой матрице стоит одно и то же число; i=1, 2, ..., m ; j=1, 2, ..., n .
Пусть A = (aij) – некоторая матрица и g–произвольное число,тогда g A = (g aij), то есть при умножении матрицы A на число g все числа, составляющие матрицу A, умножаются на число g.
Пусть A и B – матрицы одинаковой размерности A = (aij), B = (bij), тогда их сумма A + B – матрица C = (cij) той же размерности, определяемая из формулы cij= aij + bij, то есть при сложении двух матриц попарно складываются одинаково расположенные в них числа.
Матрицу A можно умножить на матрицу B, то есть найти матрицу C = AB, если число столбцов n матрицы A равно числу строк матрицы B, при этом матрица C будет иметь столько строк, сколько строк у матрицы A и столько столбцов, сколько столбцов у матрицы B. Каждый элемент матрицы C определяется формулой
![]()
Элемент cij матрицы-произведения C равен сумме произведений элементов i -строки первой матрицы- сомножителя на соответствующие элементы j -го столбца второй матрицы - сомножителя.

Таким образом, формула (1.16) является записью системы m линейных уравнений с n неизвестными в матричной форме. Ниже будет показано, что, записывая систему в сжатом виде, кроме краткости написания мы получаем и другие очень важные преимущества.
Пусть имеются две квадратные матрицы А и В одинаковой размерности.
Требуется найти матрицу X, удовлетворяющую матричному уравнению
AX = В.
О. Обратной матрицей к матрице A называется такая матрица A–1, для которой справедливы равенства:
AA –1 = A –1 A = E (1.17)
Очевидно, что A–1 – квадратная матрица того же размера, что и матрица A. Сразу заметим, что не всякая квадратная матрица имеет обратную матрицу. Матрица А имеет обратную матрицу, если detA не равно 0.
Обратная матрица имеет вид:




2. 1 2 3 И n порядок
Определение:
Матрицей
называется множество чисел, записанное
в виде таблицы, где каждому числу (
элементу матрицы) соответствует двойной
индекс, первая часть которого означает
номер строки, в которой расположено это
число, а вторая – номер столбца. Эта
таблица чисел заключается в круглые
скобки.
Матрица называется квадратной,
если количество её строк равно количеству
столбцов.
Пример:
 -
матрица А размера 3 на 3, её элемент,
например,
-
матрица А размера 3 на 3, её элемент,
например, ![]() (
1-я строка, 2-ой столбец).
(
1-я строка, 2-ой столбец).
Итак,
теперь об определителях.
Замечание: Иногда
определители называют на английский
манер детерминантами, это одно и то же
(для тех, кто знает английский язык и
подавно).
Определение
1 (простое,
для нематематических людей и
специальностей):
Определителем
матрицы называется некоторая математическая
функция элементов квадратной матрицы,
результатом которой является
число.
Обозначение:
 –
определитель 3- го порядка (т.к. матрица
размера 3 на 3) матрицы А.
Замечание:
В этом, якобы простом, определении
определителя ( звучит как тавтология)
говориться, что с элементами матрицы
нужно что то сделать ( умножить, сложить,
разделить и т.д.) и получится значение
определителя этой матрицы. Однако не
сказано. Что же все-таки надо с ними
сделать.
–
определитель 3- го порядка (т.к. матрица
размера 3 на 3) матрицы А.
Замечание:
В этом, якобы простом, определении
определителя ( звучит как тавтология)
говориться, что с элементами матрицы
нужно что то сделать ( умножить, сложить,
разделить и т.д.) и получится значение
определителя этой матрицы. Однако не
сказано. Что же все-таки надо с ними
сделать.
Вычисление
определителей первого порядка.
Матрица
размера ![]() это
просто число. Определителем такой
матрицы является само это число.
Пример:
это
просто число. Определителем такой
матрицы является само это число.
Пример:
![]()
Вычисление
определителей второго порядка.
Определитель
второго порядка (матрицы размера 2 на
2) вычисляется по правилу:
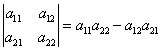 Запомнить
просто: произведение элементов, стоящих
на главной диагонали, минус произведение
элементов, стоящих на побочной.
Пример:
Запомнить
просто: произведение элементов, стоящих
на главной диагонали, минус произведение
элементов, стоящих на побочной.
Пример:
![]() .
.
Вычисление
определителей третьего порядка.
Определитель
третьего порядка вычисляется по
правилу:
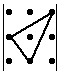
 Запомнить
порядок сомножителей, конечно же, очень
трудно, если не знать визуального
представления этого правила, которое
называется правило треугольников:
Запомнить
порядок сомножителей, конечно же, очень
трудно, если не знать визуального
представления этого правила, которое
называется правило треугольников:
 Здесь
схематично показано, какие сомножители
соседствуют в слагаемых.
Пример:
Вычислить
определитель:
Здесь
схематично показано, какие сомножители
соседствуют в слагаемых.
Пример:
Вычислить
определитель:
 Решение:
Воспользуемся
правилом треугольников.
Объясним
картинку подробно, т.е. распишем каждое
слагаемое отдельно:
Решение:
Воспользуемся
правилом треугольников.
Объясним
картинку подробно, т.е. распишем каждое
слагаемое отдельно:

![]()

![]()
![]()

![]()

![]()

![]()

Итого:
Ответ: 108
Для более точного и сложного определения и для того, чтобы говорить об определителях порядка больше третьего, потребуется вспомнить еще кое-что. Нас интересует термин подстановка, даже не столько определение, сколько способ её вычисление.
Для
подстановки принята запись:
 ,
т.е. пары чисел, записанные в столбик,
причем так, что верхние числа идут
последовательно (вообще говоря, столбцы
можно менять местами).
,
т.е. пары чисел, записанные в столбик,
причем так, что верхние числа идут
последовательно (вообще говоря, столбцы
можно менять местами).
Подстановки
бывают четными и нечетными. Для того,
чтобы выяснить, является данная
подстановка четной или нечетной, нужно
обратить внимание на вторую строку, а
точнее на порядок чисел в ней. Необходимо
подсчитать количество пар чисел во
второй строке, таких, что число, стоящее
левее, больше числа, стоящего правее
(![]() ).
Если количество таких пар нечетно, то
и подстановка называется нечетной, и,
соответственно, если количество таких
пар четно, то и подстановка называется
четной.
).
Если количество таких пар нечетно, то
и подстановка называется нечетной, и,
соответственно, если количество таких
пар четно, то и подстановка называется
четной.
Пример:
1)
![]() Рассмотрим
числа второго ряда.
4 стоит левее 3,
левее 1, левее 2 – это уже три «неправильные»
пары.
3 стоит левее 1 и 2 – еще две
пары.
Итого 5 пар, т.е. это нечетная
подстановка.
2)
Рассмотрим
числа второго ряда.
4 стоит левее 3,
левее 1, левее 2 – это уже три «неправильные»
пары.
3 стоит левее 1 и 2 – еще две
пары.
Итого 5 пар, т.е. это нечетная
подстановка.
2)
![]() Заметим,
что числа в первой строке расположены
не по порядку. Выполним перестановку
столбцов.
Заметим,
что числа в первой строке расположены
не по порядку. Выполним перестановку
столбцов.
![]() Рассмотрим
числа второго ряда.
3 стоит левее 2 и
1 – две пары,
2 стоит левее 1 – одна
пара,
5 стоит левее 4 и 1 – две пары,
4
стоит левее1 – одна пара.
Итого 6 пар
– подстановка четная.
Рассмотрим
числа второго ряда.
3 стоит левее 2 и
1 – две пары,
2 стоит левее 1 – одна
пара,
5 стоит левее 4 и 1 – две пары,
4
стоит левее1 – одна пара.
Итого 6 пар
– подстановка четная.
Определение 2 (для студентов математических специальностей, раскрывающее всю суть определяемого понятия):
Определителем
n-го порядка, соответствующим
матрице
 ,
называется
алгебраическая сумма
,
называется
алгебраическая сумма ![]() слагаемых,
составленная следующим образом:
слагаемыми служат всевозможные
произведения
слагаемых,
составленная следующим образом:
слагаемыми служат всевозможные
произведения ![]() элементов
матрицы, взятых по одному из каждой
строки и каждого столбца, причем слагаемое
берется со знаком плюс, если его индексы
составляют четную подстановку, и со
знаком минус – в противоположном
случае.
Замечание: Объясним
это определение на примере определителя
третьего порядка, для которого уже
известна формула вычисления.
.
1)
«алгебраическая сумма
слагаемых»
–
элементов
матрицы, взятых по одному из каждой
строки и каждого столбца, причем слагаемое
берется со знаком плюс, если его индексы
составляют четную подстановку, и со
знаком минус – в противоположном
случае.
Замечание: Объясним
это определение на примере определителя
третьего порядка, для которого уже
известна формула вычисления.
.
1)
«алгебраическая сумма
слагаемых»
– ![]() .
И да, действительно, здесь шесть
слагаемых.
2) «слагаемыми служат
всевозможные произведения элементов
матрицы, взятых по одному из каждой
строки и каждого столбца» – рассмотрим
например слагаемое
.
И да, действительно, здесь шесть
слагаемых.
2) «слагаемыми служат
всевозможные произведения элементов
матрицы, взятых по одному из каждой
строки и каждого столбца» – рассмотрим
например слагаемое ![]() .
Его первый множитель взят из второй
строки, второй – из первой, а третий из
третьей. То же самое и со столбцами –
первым множитель из первого столбца,
второй из третьего, а последний из
второго.
3) «причем слагаемое берется
со знаком плюс, если его индексы составляют
четную подстановку, и со знаком минус
– в противоположном случае» – рассмотрим
для примера слагаемые
.
Его первый множитель взят из второй
строки, второй – из первой, а третий из
третьей. То же самое и со столбцами –
первым множитель из первого столбца,
второй из третьего, а последний из
второго.
3) «причем слагаемое берется
со знаком плюс, если его индексы составляют
четную подстановку, и со знаком минус
– в противоположном случае» – рассмотрим
для примера слагаемые ![]() (со
знаком плюс) и
(со
знаком плюс) и![]() (со
знаком минус).
(со
знаком минус).
Составим
перестановки так, что в первой строке
будут номера строк сомножителей, а во
второй – номера столбцов.
Для
слагаемого
: ![]() (
первый столбец – индекс первого
сомножителя и т.д.)
Для
слагаемого
:
(
первый столбец – индекс первого
сомножителя и т.д.)
Для
слагаемого
: ![]() .
Определим
четность этих перестановок:
а)
–
элементы в первой строке стоят по
порядку. Во второй строке не по порядку
стоят пары:
2 левее 1 – одна пара,
3
левее 1 – одна пара.
Итого две пары,
т.е. количество пар четно, значит
перестановка четная, а значит, слагаемое
должно входить в сумму со знаком плюс
(как оно и есть на самом деле).
б)
–
элементы в первой строке стоят по
порядку. Во второй строке не по порядку
стоят пары:
2 левее 1 – одна пара.
Итого,
количество пар чисел, стоящих так, что
большее левее меньшего – 1 шт., т.е.
нечетно, а значит и перестановка
называется нечетной, и соответствующее
слагаемое должно входить в сумму со
знаком минус ( да, это так).
Пример («Сборник
задач по алгебре» под ред. А.И. Кострикина,
№1001):
.
Определим
четность этих перестановок:
а)
–
элементы в первой строке стоят по
порядку. Во второй строке не по порядку
стоят пары:
2 левее 1 – одна пара,
3
левее 1 – одна пара.
Итого две пары,
т.е. количество пар четно, значит
перестановка четная, а значит, слагаемое
должно входить в сумму со знаком плюс
(как оно и есть на самом деле).
б)
–
элементы в первой строке стоят по
порядку. Во второй строке не по порядку
стоят пары:
2 левее 1 – одна пара.
Итого,
количество пар чисел, стоящих так, что
большее левее меньшего – 1 шт., т.е.
нечетно, а значит и перестановка
называется нечетной, и соответствующее
слагаемое должно входить в сумму со
знаком минус ( да, это так).
Пример («Сборник
задач по алгебре» под ред. А.И. Кострикина,
№1001):
Выяснить,
какие из следующих произведений входят
в развернутое выражение определителей
соответствующих порядков и с какими
знаками.
а) ![]() Обратим
внимание на часть определния «по одному
из каждой строки и каждого столбца».
Все первые индексы сомножителей различны
от 1 до 6( 1, 2, 3, 4, 5, 6). Все вторые индексы
сомножителей различны от 1 до 6 ( 3, 2, 1, 4,
5, 6).
Вывод – это произведение входит
в развернутое выражение определителя
6-го порядка.
Определим знак этого
слагаемого, для этого составим перестановку
из индексов сомножителей:
Обратим
внимание на часть определния «по одному
из каждой строки и каждого столбца».
Все первые индексы сомножителей различны
от 1 до 6( 1, 2, 3, 4, 5, 6). Все вторые индексы
сомножителей различны от 1 до 6 ( 3, 2, 1, 4,
5, 6).
Вывод – это произведение входит
в развернутое выражение определителя
6-го порядка.
Определим знак этого
слагаемого, для этого составим перестановку
из индексов сомножителей:
![]()
3 левее 2, 1 – две пары, 2 левее 1 – одна пара, 6 левее 5, 4 – две пары, 5 левее 4 – одна пара. Итого 6 пар, т.е. перестановка четная и слагаемое входит в развернутую запись определителя со знаком «плюс».
б) ![]() Все
первые индексы сомножителей различны
от 1 до 5( 3, 1, 5, 4, 2). Все вторые индексы
сомножителей различны от 1 до 5 (1, 3, 2, 5,
4).
Вывод – это произведение входит
в развернутое выражение определителя
5-го порядка.
Определим знак этого
слагаемого, для этого составим перестановку
из индексов сомножителей:
Все
первые индексы сомножителей различны
от 1 до 5( 3, 1, 5, 4, 2). Все вторые индексы
сомножителей различны от 1 до 5 (1, 3, 2, 5,
4).
Вывод – это произведение входит
в развернутое выражение определителя
5-го порядка.
Определим знак этого
слагаемого, для этого составим перестановку
из индексов сомножителей:
![]() Переставим
столбцы так, чтобы числа в первой строке
шли по порядку от меньшего к большему.
Переставим
столбцы так, чтобы числа в первой строке
шли по порядку от меньшего к большему.
![]() 3
левее 1, 2 – две пары.
4 левее 1, 2 – две
пары,
5 левее 2 – одна пара.
Итого
5 пар, т.е. перестановка нечетная и
слагаемое входит в развернутую запись
определителя со знаком «минус».
в)
3
левее 1, 2 – две пары.
4 левее 1, 2 – две
пары,
5 левее 2 – одна пара.
Итого
5 пар, т.е. перестановка нечетная и
слагаемое входит в развернутую запись
определителя со знаком «минус».
в) ![]() –
обратим внимание на первый и шестой
сомножители:
–
обратим внимание на первый и шестой
сомножители: ![]() и
и ![]() .
Они оба взяты из 4-го столбца, а значит,
это произведение не может входить в
развернутое выражение определителя
7-го порядка.
.
Они оба взяты из 4-го столбца, а значит,
это произведение не может входить в
развернутое выражение определителя
7-го порядка.
