20. Оптимизационные модели на основе межотраслевого баланса.

Простейшая оптимизационная модель межотраслевого баланса:

max, ^*

y >= 0, ^**

т.е. Цель – получение максимального ВВП со стороны спроса, m – число отраслей, y_i – конечное использование i-той отрасли.

Целевая функция в векторном виде: (Е; у)→ max, где Е – m-мерный единичный вектор (1;1;m;1).

На практике в оптим. плане для нек. отраслей конеч. исп-ие= 0. Для вектора конечного использования необходимо задать верхнюю и нижнюю границу: условие ^** заменить на ^***.

*** d_-<= y <= d₊ , где d_{- и} d_{+ -} вектора, задающие нижн. и верх. границу.

Вместо условия *** можно задавать строгие сдвиги в экономике:

X >= (1+ )*

- x >= - (1 - )*

, где - вектор валового выпуска в 1 отрасли

= ( ₁, ₂, … _n)

= ( _{1, 2, … n}) – вектор ВВ за пред. Год

• - темп перестройки отрасли

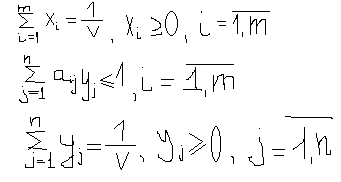
Рассмотрим равенство

Т.к. 1й игрок максимизирует V, то он одновременно минимизирует при ограничении , x_i >0, i =1..m

Рассмотрим равенство

Т.к. 2й игрок стремится к минимизации V, то сумму надо макс-ть. Т.о.

Т.о. нужно решить две оплтимизационные задачи линейного программирования. Из теории двойтвенности вытекает, что эти задачи разрешимы. Их можно решить симплекс-методом.

Допустим, если решили первую задачу и получили оптим. план x^* = (x₁^*, x₂^*,…, x_m^*).

Тогда решаем 2ую задачу и получаем

y^* = (y₁^*, y₂^*,…y_n^*)

Затем вычисляем цену

x* =

Оптим. смеш. стратегия

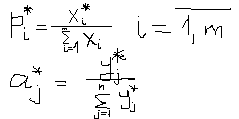
Это есть основная теорема матричной теории выбора

21. Агрегирование моб.

Пусть эк-ская сис-ма состоит из n отраслей. Пусть данные отрасли разбиты на m подмножеств J₁, J₂,…, J_m (m<n). Пересечение любой пары этих подмножеств дает  (пустое множество).

Для любых p и q (p≠q): J_p∩J_q=,

J_p={1,2,m,n}

1. Стоим массив М (l, k, )

l- индекс исходной отрасли

k- индекс агрег. Отрасли, в кот-ую входит отрасль l

- весовой коэф.

2. Вычисляются две матрицы

T= ‌‌‌‌‌‌‌‌‌‌‌‌│t_lk│_{m x n}

G= ‌‌‌‌‌‌‌‌‌‌‌‌│g_lk│_{m x n}

t_{lk =} 1_, если отрасль l принадлежит J_k

0, если l не принадлежит J_k

g_{lk =} , если (l, k, ) принадлежит М

0, если (l, k, ) не принадлежит М

3. Вычисляется матрица:

• = T*A*G – матрица прямых затрат для М отраслей

• = T*y – вектор конеч. использования для М отр-й

4. Решаем систему:

• = * +

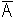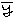
Если выполняются 2 условия:

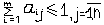1. причем хотя бы одно из неравенств строгое

2. 

То решение агрегированной модели является обоснованным

Вопрос 22. Модель прогноза межотраслевых связей.

Как спрогнозировать коэф-ты прямых затрат

Строим оптимизационную модель

(6)

- матрица коэф-в пр. затрат за отч. год.

Ограничения:

(7)

(8) (9)

- коэф-ты пр. затрат для прогнозного года

- ПП -й отр. прогноз. года

- оценка пром. затрат -й отрасли прогн. года

Осн. вопрос – каким усл-ям должны удовлетворять заданные величины, чтобы мн-во реш-й с-мы пустое мн-во.

Условия баланса:

чтобы задача имела допустимые решения (необх. и дост.)

Док-во. Необх-ть.

У нас имеется нек. реш-е, удовл-е усл-ю. Сложим рав-ва (7) и (8) будет вып-ся балансов. ур-е.

Достаточность. Если вып-ся усл-е баланса, покажем, что сущ. хотя бы 1 допуст. план. Дост-но убед-ся, что точка

Покажем, что будет вып-ся рав-во (7)

(т.к. ) чтд (анал-но док-ся, что матрица уд-ет усл-ю 8)

Ф-я выпуклая, т.к. все миноры, составл-е по 2-й произв-й >0. Т.е. локальный min явл-ся и глобальным.