2.5. Изоморфизм графов

Один и тот же граф геометрически можно изобразить различными способами. Так, на рис.2.9 приведены изображения одного и того же графа. Такие графы называют изоморфными.

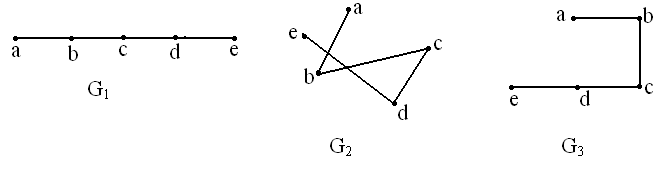Рис. 2.9.

В связи с этим возникает следующая задача. Если имеется два изображения графов, то как узнать, не представляют ли они собой один и тот же граф? Ответить на этот вопрос сразу достаточно трудно. На практике обычно предварительно определяют некоторые параметры обоих графов. Такими параметрами могут быть число вершин, число ребер, число компонент связности, последовательность степеней вершин в убывающем порядке. Если какие-то из этих параметров у двух графов различны, то эти графы различны. Однако, если все параметры у двух графов совпали, то это не гарантирует, что графы изоморфны. Например, на рис. 2.10. приведены два графа, у которых все параметры совпадают, и тем не менее они различны.

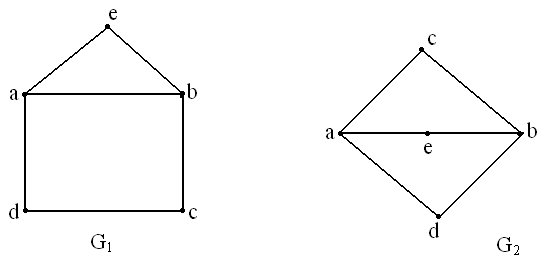
Рис. 2.10.

2.6. Отношение порядка и отношение эквивалентности на графе

Граф дает удобное геометрическое представление отношений на множестве, поэтому теория графов и теория отношений на множестве взаимно дополняют друг друга.

На графе G=(X, Г) введено отношение порядка, если для любых двух вершин (х и y), удовлетворяющих условию , существует путь из х в у. В этом случае говорят, что вершина х предшествует вершине у, или что вершина у следует за вершиной х.

Данное определение отражает на графе все свойства отношения порядка.

Рефлексивность. Условие

истинно 2.12

означает эквивалентность вершины самой себе, т.е. условие . Однако при желании это условие можно рассматривать как наличие пути из х в х, т.е. как петлю в вершине х (рис.2.11 а).

Транзитивность. Условие

2.13

означает, что вершины х, у, z последовательно встречаются на одном и том же пути (рис. 2.11 б).

Антисимметричность.

2.14

Левая часть этого выражения говорит о том, что существует путь из х в у, а так же существует путь из у в х. Но это означает, что в графе имеется контур, на котором лежат вершины х и у (рис.2.11 в).

Из правой части условия 2.14 вытекает, что вершины, лежащие на одном и том же контуре, являются эквивалентными. Будем рассматривать этот вывод как определение эквивалентности на графе и покажем, что такое определение удовлетворяет всем трем условиям отношения эквивалентности. Условия рефлексивности и симметрии являются очевидными и вытекают из данного выше определения эквивалентности. Условие транзитивности также является очевидным, так как говорит о том, что если в графе имеется контур с вершинами х и у, а так же контур с вершинами у и z, то имеется и контур, на котором лежат вершины х и z (рис.2.11 в).

Таким образом, отношение порядка совместно с отношением эквивалентности определяет некоторый граф.

На графе может быть так же введено отношение строгого порядка. В этом случае для любых двух вершин (х и у), удовлетворяющих условию x<y, существует путь, идущий из х в у. Условие транзитивности означает, как и в предыдущем случае, что вершины х, у и z встречаются последовательно на одном и том же пути. Условие антирефлексивности (х<x ложно) говорит об отсутствии петель на графе, а условие несимметрии (x<y, y<x взаимоисключается) говорит об отсутствии контуров.

Таким образом, отношение строгого порядка определяет граф без контуров.