Стереометрия

Н.С. Шабрыкина

Прямые и плоскости в пространстве

1. Введение

Стереометрия – это раздел геометрии, изучающий пространство. Пространством в элементарной геометрии называется множество, элементы которого называются точками и в котором выполнены аксиомы стереометрии. Элементы этого множества называются точками.

Расстояниями называются величины, соответствующие каждым двум точкам пространства так, что выполнены аксиомы стереометрии.

Плоскостью в пространстве называется содержащаяся в нем фигура, на которой выполнена планиметрия и для которой справедливы аксиомы стереометрии.

Прямой называется фигура на плоскости, для которой вместе с другими такими фигурами выполняются аксиомы планиметрии.

Как видно, эти определения не конструктивные. Они лишь говорят о том, что вводится ряд некоторых связанных между собой объектов, которые будут обладать определенными свойствами. Стереометрия, как и любая наука строится на основе аксиом и определений. Остальные выводы получаются из них с помощью логических рассуждений и формулируются в виде теорем. От того, какой набор аксиом выбрать, будет зависеть конечные результаты, получаемые с помощью данной теории. Проверка правильности предположений происходит при помощи сравнения с экспериментальными данными.

В геометрии, в отличие от многих наук, не существует всеми принятого единого набора аксиом – в разных учебниках можно встретить различные наборы аксиом – но результаты получаются те же самые. Меняется только распределение фактов между аксиомами и теоремами: т.е. что берется без доказательства, а что доказывается.

Обозначения: точки обозначают большими буквами латинского алфавита, прямые – маленькими буквами латинского алфавита, плоскости обычно обозначают малыми буквами греческого алфавита.

2. Аксиомы стереометрии

Сформулируем те аксиомы, на которых будем строить наш курс.

Аксиома 1 (аксиома плоскости). В пространстве существуют плоскости. Через каждые три точки пространства проходит плоскость.

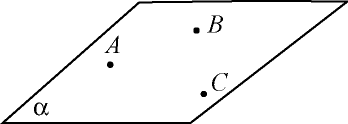
Вторую часть аксиомы плоскости можно выразить еще и так: через каждые три точки можно провести плоскость – или так: любые три точки лежат в одной плоскости.

Обратите внимание, что в аксиоме 1 говорится «существуют плоскости», т. е. что плоскостей в пространстве больше одной.

Аксиома 2 (аксиома пересечения плоскостей). Если две плоскости имеют общую точку, то их пересечение есть их общая прямая.

Замечание. То, что пересечение двух плоскостей есть их общая прямая, означает, что она является прямой как на одной, так и на другой плоскости. Кроме того, у этих плоскостей нет общих точек вне их общей прямой.

Две плоскости, имеющие общую точку (и тем самым общую прямую), называются пересекающимися плоскостями.

Аксиома 3 (аксиома принадлежности прямой плоскости). Если прямая проходит через две точки данной плоскости, то она лежит в этой плоскости.

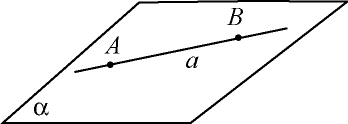
Другими словами, если две точки данной прямой принадлежат данной плоскости, то прямая содержится в этой плоскости.

Из этой аксиомы следует, что если прямая не лежит в данной плоскости, то она имеет с ней не более одной общей точки.

Прямая и плоскость, имеющие единственную общую точку, называются пересекающимися.

Аксиома 4 (аксиома планиметрии). На любой плоскости выполняется планиметрия.

3. Способы задание плоскости

Рассмотрим несколько способов задания плоскости. Для этого докажем следующие теоремы.

Теорема 3.1. Через три точки, не лежащие на одной прямой, проходит плоскость и притом только одна.

Доказательство. Пусть точки А, В, С не лежат на одной прямой. По аксиоме плоскости через каждые три точки проходит плоскость. Поэтому есть плоскость, проходящая через точки А, В, С; обозначим ее . Убедимся, что она только одна.

Допустим, что через данные точки проходит еще одна плоскость , отличная от . Плоскости и имеют общие точки. По аксиоме 2 пересечением плоскостей является их общая прямая. Значит, эта прямая содержит все три точки общие для этих плоскостей. Но это противоречит условию теоремы, так как точки не лежат на одной прямой. Итак, через три точки проходит лишь одна плоскость.

Следствие. В пространстве существуют четыре точки, не лежащие в одной плоскости. Для каждых двух точек можно подобрать еще две точки так, что все четыре не лежат в одной плоскости.

Теорема 3.2. Через прямую и не лежащую на ней точку проходит плоскость и притом только одна.

Доказательство. Пусть даны прямая и не лежащая на ней точка А. Возьмем на прямой две точки В и С. Через три точки А, В, С, не лежащие на одной прямой, согласно теореме 1 проходит единственная плоскость. Прямая а имеет с ней две общие точки и, значит, по аксиоме 3 лежит на ней.

Теорема 3.3. Через две пересекающиеся прямые проходит плоскость и притом только одна.

Доказательство. Выберем на прямой точку , не являющуюся точкой пересечения прямых и . Эта точка не лежит на прямой по построению. Проведем через прямую и точку плоскость. По теореме 2 эта плоскость существует и единственная.

Доказанные выше теоремы указывают три способа задания плоскости:

1. тремя точками, не лежащими на одной прямой;

2. прямой и не лежащей на ней точкой;

3. двумя пересекающимися прямыми.

Из доказанных утверждений вытекает, что через каждую прямую в пространстве проходит сколь угодно много плоскостей.