1. Функция f (отображение, операция, оператор) — это закон или правило, согласно которому каждому элементу x из множества X ставится в соответствие единственный элемент y из множества Y

Определение предела по Коши. Число A называется пределом функции f (x) в точке a, если эта функция определена в некоторой окрестности точки a за исключением, быть может, самой точки a, и для каждого ε > 0 существует δ > 0 такое, что для всех x, удовлетворяющих условию |x – a| < δ, x ≠ a, выполняется неравенство |f (x) – A| < ε.

Определение предела по Гейне. Число A называется пределом функции f (x) в точке a, если эта функция определена в некоторой окрестности точки a за исключением, быть может, самой точки a, и для любой последовательности такой, что сходящейся к числу a, соответствующая последовательность значений функции сходится к числу A

2.Функция y=f(x) наз-ся непрерывной в т.а,если в точке а предел дельта у при дельта х стремящемся к 0 равен 0.

Функция y=f(x) наз-ся непрерывной на интервале (а;b),если она непрерывна в любой его точке.

Функция y=f(x) наз-ся непрерывной на отрезке [a;b],если она непрерывна в интервале (a,b) непрерывна справа в т. х=b ,слева в т. х=а.

3. 1-й замечательный предел 2-й замечательный предел

5.

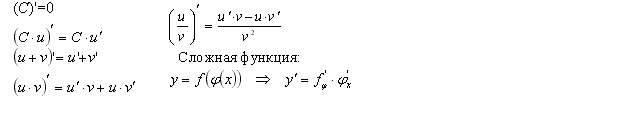
6. Если f '(x) — производная функции f (x), то производная от нее по независимой переменной x, (f '(x))' = f ''(x), называется производной второго порядка. Аналогично определены производные 3-го, 4-го, , и т.д, n-го порядка: f''' (x) = ( f'' (x))' , f (4)(x) = (f''' (x))' , f (n)(x) = (f (n -1)(x))' .

7.Функция y=f(x) наз-ся дифференцируемой в т. Х области Д,если в этой точке приращение ф-и можно представить в виде:

Δy=A·Δx+α(Δx)·Δx, где A -- некоторое число, независящее от Δx, а α(Δx)-- бесконечно малая функция от переменной Δx, т.е

Связь дифференцируемости с непрерывностью функции в точке. Если функция дифференцируема в некоторой точке, то в этой точке функция непрерывна.

Связь диф-ти с сущ-ем производной

Функция дифференцируема в т.х,когда имеет в этой точке конечную производную

8. Дифференциал ф-и в т.х называется число, обозначающееся символом dy и равное

Dy=f’(x)* Δx

Геом. смысл: дифференциал функции у=ƒ(х) в точке х равен приращению ординаты касательной к графику функции в этой точке, когда х получит приращение ∆х.

4. Производной f’(x) функции y=f(x) в т.х наз-ся конечный предел ,если он сущ-ет .

Производная - основное понятие дифференциального исчисления, характеризующее скорость изменения функции. Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если таковой предел существует

Геометрический смысл: производная   равна тангенсу угла наклона касательной к графику функции   в точке  .

) Геометрический смысл производной.

Пусть – некоторая кривая, – точка на кривой .

Любая прямая, пересекающая не менее чем в двух точках называется секущей.

Касательной к кривой в точке называется предельное положение секущей  ,  если точка стремится к ,  двигаясь по кривой.

Из определения очевидно, что если касательная к кривой в точке существует, то она единственная

Рассмотрим кривую y = f(x)  (т.е. график функции  y = f(x)).  Пусть в точке он имеет невертикальную касательную .  Ее уравнение: (уравнение прямой, проходящей через точку и имеющую угловой коэффициент  k).

По определению углового коэффициента , где – угол наклона прямой   к оси .

Пусть – угол наклона секущей к оси ,  где  . Так как – касательная, то при

⇒ ⇒   .

Следовательно,

.

Таким образом, получили, что – угловой коэффициент касательной к графику функции y = f(x) в точке (геометрический смысл производной функции в точке).  Поэтому уравнение касательной к кривой y = f(x) в точке можно записать в виде

 

      Замечание. Прямая, проходящая через точку перпендикулярно касательной, проведенной к кривой в точке , называется нормалью к кривой в точке . Так как угловые коэффициенты перпендикулярных прямых связаны соотношением ,  то уравнение нормали к кривой y = f(x) в точке будет иметь вид

,  если .

Если же , то касательная к кривой y = f(x) в точке будет иметь вид , а

9. Прямая x = a называется вертикальной асимптотой графика функции f (x) при x → a, если выполнено хотя бы одно из условий 

 , 

П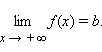 рямая y = b называется горизонтальной асимптотой графика функции f (x) при x → +∞, если 

Прямая y = kx + b, k ≠ 0 называется наклонной асимптотой графика функции f (x) при x → +∞, если 

10.Ф-я монотонная на интервале (a,b),если она на этом интервале явл-ся или возрастающей, или убывающей, или невозраст, или неубывающей.

Точки максимума и минимума ф-и называются точками экстремума

.

11. График функции y=f(x) называется выпуклым на интервале (a; b), если он расположен ниже любой своей касательной на этом интервале.

График функции y=f(x) называется вогнутым на интервале (a; b), если он расположен выше любой своей касательной на этом интервале.

Точка, при переходе через которую функция меняет выпуклость на вогнутость или наоборот, называется точкой перегиба. f '' ( x₀ ) = 0.

13. Совокупность всех первообразных функции   называется неопределенным интегралом от   и обозначается  .

Св-ва неопределённого интеграла:

14. Операция нахождения неопределенного интеграла данной функции f(x) на некотором промежутке наз.интегрированием функции f(x).

С помощью таблиц: вычисляемый интеграл окажется один из табличных интегралов,в этом случае для нахождения такого интеграла требуется безошибачно найти соответствующую формулу таблицы и ею воспользоваться.

Метод разложения: интеграл,предложенный для вычисления после применения линейных свойств неопределенного интеграла заменяется линейной комбинацией табличных интегралов.

16. Метод замены переменной (метод подстановки)

Метод интегрирования подстановкой заключается во введении новой переменной интегрирования (то есть подстановки). При этом заданный интеграл приводится к новому интегралу, который является табличным или к нему сводящимся. Общих методов подбора подстановок не существует. Умение правильно определить подстановку приобретается практикой.

Пусть требуется вычислить интеграл   Сделаем подстановку   где   — функция, имеющая непрерывную производную.

Тогда   и на основании свойства инвариантности формулы интегрирования неопределенного интеграла получаем формулу интегрирования подстановкой:

17.Интегрирование по частям.

Теорема. Пусть функции u=u(x) и v=v(x) дифференцируемы на некотором интервале (а;в). Пусть на (а;в) функции v(x)*u’(х) имеет первообразную, тогда на интервале (а;в) функция v’(x)*u(x) так же имеет первообразную, при этом справедливо равенство ∫u(x)*v’(x)dx=u(x)*v(x) - ∫u’(x)*v(x)dx (1).

Замечание. Определение дифференциала и свойство инвариантности его формы позволяют придать формуле (1) следующий вид ∫u*dv=u*v - ∫v*du (2).

Интегралы, вычисляемые таким методом:

1)интегралы, к которых подынтегральная функция содержит одну из следующих функций: arcsinX, lnX, arccosX, arctgX, arcctgX, ln²X, lnu(x), arcsin²X, arccos²X, arctg²X, arcctg²X. При условии. Что оставшаяся часть подынтегральной функции представляет собой производную известной функции.

2)интегралы вида:

1.∫(ax+b)ⁿ*cosXdx; 2. ∫(ax+b)ⁿ*sinXdx; 3.∫(ax+b)ⁿ*e^axdx; 4.∫(ax+b)ⁿ*a^αxdx, при а,в=const.

Эти интегралы беруться путем последовательного n-кратного применения формулы (1) или (2), где всякий раз в качестве u(x) надо выбирать а+в в соответствующей степени. После каждого интегрирования эта степень будет уменьшаться на единицу.

3)∫e^αx*cosβxdx; ∫e^αx*sinβxdx; ∫a^αx*cosβxdx; ∫a^αx*sinβxdx; ∫sin(lnX)dx; ∫cos(lnX)dx, при α,β,а=const.

Такие интегралы берутся в двухкратном интегрировании по частям, при любом выборе u(x).

15. Пусть требуется вычислить

Предположим, что существуют дифференцируемые функции и , такие, что тогда

Указанное преобразование подынтегрального выражения называют подведением под знак дифференциала.

Например. .

Замечание. При интегрировании методом подведения под знак дифференциала бывают полезны следующие равенства:

1. ;

2. ;

3. ;

4. ;

5. ;

6. ;

7. ;

8. ;

9. ;

10. ;

11. .

19. Понятие определённого интеграла

Определённым интегралом от непрерывной функции f(x) на конечном отрезке [a, b] (где ) называется приращение какой-нибудь её первообразной на этом отрезке. При этом употребляется запись

Числа a и b называются соответственно нижним и верхним пределами интегрирования, а отрезок [a, b] – отрезком интегрирования.

Таким образом, если F(x) – какая-нибудь первообразная функция для f(x), то, согласно определению,

            (38)

При a = b по определению принимается

Равенство (38) называется формулой Ньютона-Лейбница. Разность F(b) – F(a) кратко записывают так:

Поэтому формулу Ньютона-Лейбница будем записывать и так:

                   (39)

Докажем, что определённый интеграл не зависит от того, какая первообразная подынтегральной функции взята при его вычислении. Пусть F(x) и Ф(х) – произвольные первообразные подынтегральной функции. Так как это первообразные одной и той же функции, то они отличаются на постоянное слагаемое: Ф(х) = F(x) + C. Поэтому

Тем самым установлено, что на отрезке [a, b] приращения всех первообразных функции f(x) совпадают.

Таким образом, для вычисления определённого интеграла необходимо найти любую первообразную подынтегральной функции, т.е. сначала следует найти неопределённый интеграл. Из всех первообразных для f(x) выбирается обычно та, которая соответствует равной нулю производной постоянной, и к ней применяется формула Ньютона-Лейбница.