
2.3 Корректировка оптимального плана по продукции
Пусть вводилась в плановое ограничение типа и имеет смысл перевыполнения плана или превышение выпуска продукции над гарантированным.
Определение 1 Гарантированный выпуск – это минимально возможный выпуск, соответствующий выполнению планового ограничения на равенстве и переменная не вошла в базис, то есть .
2.3.1 Рассмотрим как ведет себя при увеличении плана, то есть . Тогда из исходной системы будем иметь:
или
Таким образом, при увеличении гарантированного выпуска перевыполнение плана увеличивается на ту же величину и .
Запишем условие неизменности базиса:
При имеем аналогично (6):
(10)
Найдем верхнюю границу гарантированного выпуска:
(11)
2.3.2 Рассмотрим, как ведет себя при уменьшении плана, то есть .
Запишем из исходной системы:
или
Таким образом, при уменьшении гарантированного выпуска перевыполнение плана уменьшается на ту же величину и становится отрицательным, то есть .
Тогда аналогично (4) имеем:
(12)
Отсюда нижняя граница гарантированного выпуска равна:
(13)
Объединяя (10) и (12) получим допустимый интервал варьирования переменной, означающей перевыполнение плана:
(14)
Объединяя (11) и (13) получим пределы изменения гарантированного выпуска:
13.Понятие ПФ, экономическая интерпретация; параметрическая задача ЛП, пример.
Определение
1 ПФ
(производственная
функция) –
это аналитическая или табличная
зависимость производственного показателя
(результирующая функция эффекта) от
производственных факторов:
![]() .
.
ПФ используется для того, чтобы отследить динамику реакции реального производства на изменение значения производственного фактора.
Параметрическая ЗЛП
1) Линейная модель оптимизации производственной программы предприятия:
![]() (1)
(1)
![]() ,
,
![]() (2)
(2)
![]() ,
,
![]() (3)
(3)
![]() ,
,
![]() (4)
(4)
– ресурсные ограничения.
14.Линейная модель оптимизации производственной программы с учетом возможностей пополнения ресурсов и (или) изменения плановых заданий.
1) Линейная модель оптимизации производственной программы предприятия:
(1)
, (2)
, (3)
, (4)
– ресурсные ограничения.
Дополним
общую постановку модели следующим
образом: исходя из заданного объема
инвестиций V,
стоимости единицы
![]() -го
ресурса, оценить реакцию производства
на увеличение дефицитности ресурса
-го
ресурса, оценить реакцию производства
на увеличение дефицитности ресурса
2) Линейная модель оптимизации производственной программы с учетом возможностей пополнения дефицитных ресурсов в пределах заданных объемов денежных вложений. Следует учесть, что инвесторы идут на финансирование капитальных вложений. Задан коэффициент эффективности капитальных вложений εn, который служит для соотношения капитальных затрат к текущим. С учетом дополнительных условий модель примет вид:
![]() (5)
(5)
![]() ,
(6)
,
(6)
, (7)
![]() (8)
(8)
,
,
![]() ,
(9)
,
(9)
Здесь s-индекс значения параметра.
![]() могут
быть взяты =0, , то есть начальных фондов
ресурсов нет. Меняя s,
получим набор ПФ – доход от параметра
– объем инвестиций, то есть получим
зависимость эффекта от капвложений.
Когда меняем значения параметра, удобно
использовать корректировку оптимального
плана по дефицитному ресурсу. В этом
случае следует проверить предел верхнего
варьирования ресурса и если он меньше
шага по ресурсу, то можно не считать
задачу симплекс-методом, а скорректировать
решение предыдущего шага.
могут
быть взяты =0, , то есть начальных фондов
ресурсов нет. Меняя s,
получим набор ПФ – доход от параметра
– объем инвестиций, то есть получим
зависимость эффекта от капвложений.
Когда меняем значения параметра, удобно
использовать корректировку оптимального
плана по дефицитному ресурсу. В этом
случае следует проверить предел верхнего
варьирования ресурса и если он меньше
шага по ресурсу, то можно не считать
задачу симплекс-методом, а скорректировать
решение предыдущего шага.
15.Основные типы производственно-экономических задач динамического программирования (ДП).
Тип 1 Оптимальное распределение фиксированного количества ресурса по вариантам производства, различающимся во времени, в пространстве и по технологиям.
Постановка задачи:
Имеется
количество
![]() некоторого ресурса,
который можно использовать в
некоторого ресурса,
который можно использовать в
![]() вариантах производства. Известны функции
эффекта, получаемого в
-м
варианте при использовании ресурса в
количестве
вариантах производства. Известны функции
эффекта, получаемого в
-м
варианте при использовании ресурса в
количестве
![]() .
Необходимо так распределить
по
вариантам, чтобы суммарный эффект был
максимален.
.
Необходимо так распределить
по
вариантам, чтобы суммарный эффект был
максимален.
Модель:
![]()
![]() (1)
(1)
![]()
Тип 2 Оптимальное распределение производства некоторого количества продукции по вариантам производства, различающимся во времени, в пространстве и по технологиям.
Постановка задачи:
Надо
произвести заданное количество
продукции. Имеется
вариантов производства. Известны функции
затрат на производство в
-м
варианте
![]() -го
количества продукции –
-го
количества продукции –
![]() .
Необходимо так распределить требуемый
объем производства
по вариантам, чтобы суммарные затраты
были минимальны.
.
Необходимо так распределить требуемый
объем производства
по вариантам, чтобы суммарные затраты
были минимальны.
Модель:
![]()
![]() (2)
(2)
Тип 3 Оптимальное распределение воспроизводимого ресурса.
Постановка задачи:
Имеется начальное количество некоторого ресурса, который можно использовать в производстве в течение циклов. Для каждого цикла известно:
а) эффект от использования в -м цикле ресурса в количестве – ;
б)
количество ресурса, которое в
-м
цикле воспроизводится и пополняет
оставшиеся запасы –
![]() .
.
Необходимо так распределить ресурс по циклам производства, чтобы с учетом его возврата получить максимум суммарного эффекта за циклов производства.
Модель:
![]()
![]() (3)
(3)
![]()
Очевидно,
что если
![]() ,
то задача типа 3 преобразуется в задачу
типа 1.
,
то задача типа 3 преобразуется в задачу
типа 1.
Пусть
![]() ,
тогда получим:
,
тогда получим:
![]()
![]()
Из последнего: .
14.Табличный метод решения задач ДП.
Табличный метод для трехшагового процесса оптимизации (не воспроизводимый ресурс)
Пример:
Для предприятия выделен объем инвестиций в размере 2000 единиц, который нужно освоить за 3 года с максимальным эффектом. Функции эффекта от вложения средств заданы таблично с шагом по объему вложений, равным 250 единиц. Объем вложений в каждый год для предприятия не должен превышать 1250 единиц, шаг = 250. Найти оптимальный график освоения инвестиций.
Таблица 5.4
|
0 |
250 |
500 |
750 |
1000 |
1250 |
|
0 |
20 |
36 |
50 |
62 |
72 |
|
0 |
22 |
38 |
50 |
60 |
68 |
|
0 |
19 |
31 |
43 |
64 |
63 |
Решение:
![]()
![]()
![]()
Шаг
1 Пусть имеется одношаговый процесс для
третьего года. Задан эффект от вложения
средств (в размерах от 0 до 1250 с шагом
250 ) –
![]() .
.
–
![]() – неизвестно,
перебираем все возможные варианты.
– неизвестно,
перебираем все возможные варианты.
Таблица 5.5
|
0 |
250 |
500 |
750 |
1000 |
1250 |
|
0 |
0 250 |
0 250 500 |
0 250 500 750 |
0 250 500 750 1000
|
0 250 500 750 1000 1250 |
|
0 |
19 |
31 |
43 |
64 |
64 |
Шаг 2 Пусть имеется двухшаговый процесс распределения средств между вторым и третьим годом.
![]() –
неизвестно,
перебираем все возможные
,
при этом нужно соблюдать условие: объем
вложений в каждый год
–
неизвестно,
перебираем все возможные
,
при этом нужно соблюдать условие: объем
вложений в каждый год
![]() .
.
Опустим
возможные значения
![]()
Таблица 5.6
|
0 |
250 |
500 |
750 |
1000 |
1250 |
|
2000 |
1750 |
1500 |
1250 |
1000 |
750 |
Заметим,
что ограничение не касается
![]() – объема средств, распределяемых в
-ом
году, то есть возможна ситуация, когда
средства окажутся в избытке:
– объема средств, распределяемых в
-ом
году, то есть возможна ситуация, когда
средства окажутся в избытке:
![]() ,
но эффект берется в соответствии с тем,
сколько средств будет освоено, то есть
с
.
,
но эффект берется в соответствии с тем,
сколько средств будет освоено, то есть
с
.
Таблица 5.7
|
|
|
|
|
|
|
0 250 500 |
|
|
|
|
|
|
750 |
0 250 500 750 |
0 22 38 50 |
750 500 250 0 |
43 31 19 0 |
43 53 57 50 |
57 |
1000 |
0 250 500 750 1000 |
0 22 38 50 60 |
1000 750 500 250 0 |
64 43 31 19 0 |
64 65 69 69 60 |
69 69 |
1250 |
0 250 500 750 1000 1250 |
0 22 38 50 60 68 |
1250 1000 750 500 250 0 |
64 64 43 31 19 0 |
6 86 81 81 79 68 |
86 |
1500 |
0 250 500 750 1000 1250 |
0 22 38 50 60 68 |
1500 1250 1000 750 500 250 |
64 64 64 43 31 19 |
64 86 102 93 91 87 |
102 |
1750 |
0 250 500 750 1000 1250 |
0 22 38 50 60 68 |
1750 1500 1250 1000 750 500 |
64 64 64 64 43 31 |
64 86 102 114 103 99 |
114 |
2000 |
0 250 500 750 1000 1250 |
0 22 38 50 60 68 |
2000 1750 1500 1250 1000 750 |
64 64 64 64 64 43 |
64 86 102 114 124 111 |
124 |
Шаг 3 Имеем трехшаговый процесс распределения средств для первого, второго и третьего года.
Таблица 5.8
|
|
|
|
|
|
|
2000 |
0 250 500 750 1000 1250 |
0 20 36 50 62 72 |
2000 1750 1500 1250 1000 750 |
124 114 102 86 69 57 |
124 134 138 136 131 129 |
138 |
Суммарный максимальный эффект за три года от оптимального распределения средств равен 138 единиц.
Определим капвложения в каждый год.
Обратный ход:
При эффекте т вложения средств за три года равном
 ,
капвложения в первый год –
,
капвложения в первый год –
 ,
а объем средств на второй и третий год
,
а объем средств на второй и третий год
 .
.С
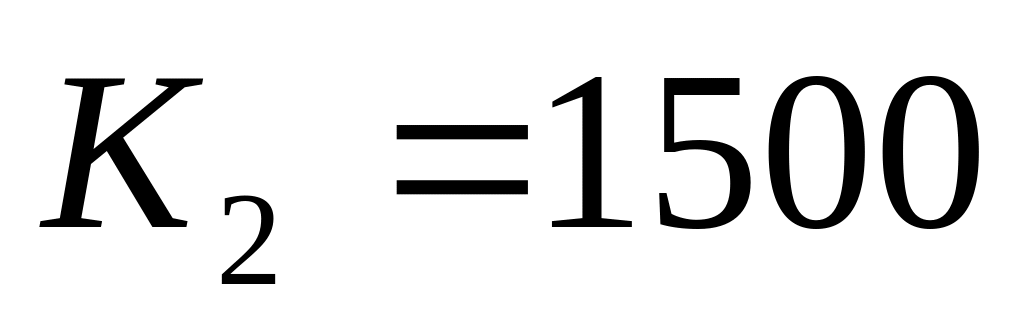 входим
в таблице второго шага и определяем
капвложения во второй год
входим
в таблице второго шага и определяем
капвложения во второй год
 ,
а объем средств на третий год
,
а объем средств на третий год
 .
Максимальный эффект за второй и третий
годы равен 102 единицы.
.
Максимальный эффект за второй и третий
годы равен 102 единицы.С входим в таблицу первого шага и определяем
 .
Эффект за третий год равен 64 единицы.
.
Эффект за третий год равен 64 единицы.
Ответ:
![]() ,
,
![]()
Таким
образом, если существует ограничение
на величину
![]() в соотношениях для
-го
шага следует брать пределы изменения
для
так:
в соотношениях для
-го
шага следует брать пределы изменения
для
так:
![]() .
.
Схема обратного хода:
|
0 |
250 |
500 |
750 |
1000 |
1250 |
|||||
|
|
|
|
|
1000 |
|
|||||
|
|
|
|
|
64 |
|
|||||
|
|
|
|
|
|
|
|||||
750 |
|
|
|
|
|
|
|||||
1000 |
|
|
|
|
|
|
|||||
1250 |
|
|
|
|
|
|
|||||
1500 |
500 |
|
2000 |
64 |
|
102 |
|||||
1750 |
|
|
|
|
|
|
|||||
2000 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
2000 |
500 |
|
1500 |
102 |
|
138 |
18.Оптимальное распределение воспроизводимого ресурса.
Для предприятия выделен объем инвестиций в размере 2000 единиц, который нужно освоить за 3 года с максимальным эффектом. Функции эффекта от вложения средств заданы таблично с шагом по объему вложений, равным 250 единиц. Объем вложений в каждый год для предприятия не должен превышать 1250 единиц, шаг = 250. Найти оптимальный график освоения инвестиций.
Таблица 5.4
|
0 |
250 |
500 |
750 |
1000 |
1250 |
|
0 |
20 |
36 |
50 |
62 |
72 |
|
0 |
22 |
38 |
50 |
60 |
68 |
|
0 |
19 |
31 |
43 |
64 |
63 |
Для условия примера 2 п.5.4.2.
Средства
в конце каждого года возвращаются в
виде части прибыли, идущей на расширение
производства в размере
![]() ,
и присоединяются к оставшимся средствам.
,
и присоединяются к оставшимся средствам.
Запишем модель:
![]()
![]()
![]()
![]()
Решение:
![]()
![]()
![]()
Шаг 1
Таблица 5.9
|
0 |
250 |
500 |
750 |
950 |
1000 |
1250 |
1500 |
1750 |
2000 |
|
0 |
0 250 |
0 250 500 |
0 250 500 750 |
0 250 500 750 950 |
1000 |
1000 |
1000 |
1000 |
1000 |
|
0 |
19 |
31 |
43 |
59,8 |
64 |
64 |
64 |
64 |
64 |
Прежде
чем перейти ко второму шагу, определим
возможные значения
![]() ;
;
;
;
![]() .
.
Таблица 5.10
|
0 |
250 |
500 |
750 |
1000 |
1250 |
|
2000 |
1850 |
1700 |
1550 |
1400 |
1250 |
Шаг 2
Таблица 5.11
|
|
|
|
|
|
|
1250 |
0 250 500 750 1000 1250 |
0 22 38 50 60 68 |
1250 1100 950 800 650 500 |
64 64 59,8 47,2 38,2 31 |
64 86 97,8 97,2 98,2 99 |
99 |
1400 |
0 250 500 750 1000 1250 |
0 22 38 50 60 68 |
1400 1250 1100 950 800 650 |
64 64 64 59,8 47,2 38,2 |
64 86 102 109,8 107,2 106,2 |
109,8 |
1550 |
0 250 500 750 1000 1250 |
0 22 38 50 60 68 |
1550 1400 1250 1100 950 800 |
64 64 64 64 59,8 47,2 |
64 86 102 114 119,8 115,2 |
119,8 |
1700 |
0 250 500 750 1000 1250 |
0 22 38 50 60 68 |
1700 1550 1400 1250 1100 950 |
64 64 64 64 64 59,8 |
64 86 102 114 124 127,8 |
127,8 |
1850 |
0 250 500 750 1000 1250 |
0 22 38 50 60 68 |
1850 1700 1550 1400 1250 1100 |
64 64 64 64 64 64 |
64 86 102 114 124 132 |
132 |
2000 |
0 250 500 750 1000 1250 |
0 22 38 50 60 68 |
2000 1850 1700 1550 1400 1250 |
64 64 64 64 64 64 |
64 86 102 114 124 132 |
132 |
для , не принадлежащего таблице первого шага, рассчитываем методом кусочно-линейной интерполяции:
![]()
![]()
![]()
![]()
![]()
Шаг
3 Строим расчетную таблицу, определяющую
оптимальные вложения в первый год
![]() и суммарный эффект за три года
.
и суммарный эффект за три года
.
Таблица 5.12
|
|
|
|
|
|
|
2000 |
0 250 500 750 1000 1250 |
0 20 36 50 62 72 |
2000 1850 1700 1550 1400 1250 |
132 132 127,8 119,8 109,8 99 |
132 152 163,8 169,8 171,8 171 |
171,8 |
![]()
На
третьем шаге получили
![]()
Обратный ход:
С
![]() входим
в таблицу второго шага и находим
входим
в таблицу второго шага и находим
![]()
С
![]() входим
в таблицу первого шага и находим
входим
в таблицу первого шага и находим
![]()
Ответ:
![]() ,
,
![]()
19.Метод множителей Лагранжа; интерпретация функции и множителей Лагранжа.
Метод множителей Лагранжа обобщен на задачи с ограничениями и условием неотрицательности неизвестных. В практическом применении метода множителей Лагранжа могут возникнуть следующие трудности:
1) трудности численного решения систем нелинейных уравнений;
2) проблема полного перебора найденных условных локальных экстремумов с целью поиска наибольшего (наименьшего) значения;
3) проблема существования локальных условных экстремумов и отсутствие глобальных условных экстремумов (многоэкстремальные задачи);
4)
обобщение метода множителей Лагранжа
на класс экстремальных задач с
ограничениями типа
![]() или
или
![]() связано с вычислительными трудностями.
связано с вычислительными трудностями.
Для
задач выпуклого программирования задачу
на условный экстремум можно свести к
задаче нахождения Седловой точки функции
Лагранжа. Функция Лагранжа
![]() это функция векторов
это функция векторов
![]() и
и
![]() таких, что в точке, где вектор
таких, что в точке, где вектор
![]() приносит локальный максимум
приносит локальный максимум
![]() ,
вектор
приносит минимум
,
вектор
приносит минимум
![]() .
В теории математического программирования
доказывается, что если конструкция
функции такова
.
В теории математического программирования
доказывается, что если конструкция
функции такова
![]() (1)
(1)
где
- нелинейная функция цели исходной
задачи,
![]() - соответствующие правые и левые части
линейных ограничений равенств, то
имеет седловую точку
- соответствующие правые и левые части
линейных ограничений равенств, то
имеет седловую точку
![]() .
.
Причем
компоненты вектора
соответствуют относительному максимуму
при ограничениях
![]() являются компонентами Седловой точки
функции Лагранжа
являются компонентами Седловой точки
функции Лагранжа
![]() .
.
Определение 2 Функция имеет в точке седловую точку, если условие:
![]() (2)
(2)
выполняется
для
в
![]() -окрестности
точки
,
а для
в
-окрестности
точки
-окрестности
точки
,
а для
в
-окрестности
точки
![]() ;
если (2) выполняется для всех
и
,
то функция Лагранжа
имеет в точке
глобальную
седловую точку.
;
если (2) выполняется для всех
и
,
то функция Лагранжа
имеет в точке
глобальную
седловую точку.
Для имеющих практическое приложение в математическом моделировании экономических процессов (квадратичная целевая функция и линейные ограничения), точка – глобальная седловая точка и компоненты соответствуют глобальному максимуму .
Из
(2) следует, что
достигает минимума в точке
,
а
![]() достигает
максимума в точке
,
то есть:
достигает
максимума в точке
,
то есть:
![]()
и аналогично
![]()
Таким образом, для соблюдается принцип максимина (минимакса).
Интерпретация множителей Лагранжа
С
седловой точкой связана теория
двойственности, в соответствии с которой
если прямая задача имеет в Седловой
точке решение
,
то
![]() является решением сопряженной задачи
и интерпретируется как двойственные
(объективно - обусловленные) оценки
ресурсов. Тогда при увеличении ресурса
является решением сопряженной задачи
и интерпретируется как двойственные
(объективно - обусловленные) оценки
ресурсов. Тогда при увеличении ресурса
![]() на
на
![]() эффект
эффект
![]() возрастает на величину
возрастает на величину
![]() .
Аналогично, если двойственная задача
имеет в Седловой точке решение
.
Аналогично, если двойственная задача
имеет в Седловой точке решение
![]() ,
то
,
то
![]() является решением сопряженной задачи
и интерпретируется как степень
напряженности плановых заданий. Тогда
при увеличении плановых заданий на
является решением сопряженной задачи
и интерпретируется как степень
напряженности плановых заданий. Тогда
при увеличении плановых заданий на
![]() на величину
на величину
![]() эффект
уменьшится на
эффект
уменьшится на
![]()
Таким
образом, компоненты вектора
![]() оптимальным
образом соотносятся между собой по
степени дефицитности ресурса
и со значением эффекта по величине
приращения эффекта от ввода в производство
единицы ресурса
оптимальным
образом соотносятся между собой по
степени дефицитности ресурса
и со значением эффекта по величине
приращения эффекта от ввода в производство
единицы ресурса![]() Это эффект, который дает единица ресурса.
Это эффект, который дает единица ресурса.
Отсюда
интерпретация
такова: значение функции Лагранжа в
Седловой точке это эффект
минус тот эффект, который мог бы быть
получен, если бы дефицитные ресурсы
были в достатке. Действительно,
![]() может
быть равно нулю, когда
может
быть равно нулю, когда
![]() ,
то есть
,
то есть
![]() -
дефицита нет; с другой стороны при
-
дефицита нет; с другой стороны при
![]() ,
есть дефицит,
,
есть дефицит,
![]()
Выводы.
Существуют различные подходы к ценообразованию, как к механизму формирования цен для различных экономических условий; рынок в условиях свободной конкуренции; частично или полностью монополизированный рынок. В последнем случае предполагается, что производственная функция будет полностью реализована и тогда в основу расчета цены берутся затраты на предполагаемый объем производства и номенклатуру продукции – это затратная концепция ценообразования.
Другой подход основан на концепции, согласно которой основным фактором формирования цены является эффект от реализации продукции. В задаче линейного программирования оценки являются решением двойственной задачи линейного программирования. Такой подход называется концепция цен оптимального плана. При этом цены, построенные на основании ООО, соотнесены с интенсивностью потребности в ресурсе и с его наличием.
В случае, когда функция цели нелинейная, те же оценки дает применение для реализации модели метода множителей Лагранжа.
Примечание: анализ выпуклых задач (обобщение на случай ограничения или ) используют разрешающие множества или множители Лагранжа:
а) для формулирования необходимо и достаточно условий того, что допустимое решение является точкой экстремума (локального, а значит и глобального);
б) для проверки оптимальности допустимого решения и, в случае неоптимальности, для определения направления, в котором нужно производить изменение решения.
20.Частные задачи ЛП: задача о смесях.
Постановка задачи:
Имеется
продуктов,
![]() .
Каждый
-ый
продукт характеризуется содержанием
в единице продукта (веса, объема) некоторых
активных веществ (белки, жиры, химические
элементы и т.д.); всего компонент имеется
.
Каждый
-ый
продукт характеризуется содержанием
в единице продукта (веса, объема) некоторых
активных веществ (белки, жиры, химические
элементы и т.д.); всего компонент имеется
![]() ,
,
![]() ;
;
– содержание -го питательного вещества в единице -го продукта.
Известны: физиологический норматив -го вещества – и цена единицы продукта – .
Определить количество -го продукта в смеси – такое, чтобы стоимость смеси была минимальной и выполнялись требования по содержанию в ней активных веществ.
Модель:
Обозначим
– количество
-го
продукта, включаемого в смесь; тогда
![]() будет выражать состав и количество
продуктов и , таким образом, саму смесь.
будет выражать состав и количество
продуктов и , таким образом, саму смесь.
![]() (1)
(1)
![]()
21.Частные задачи ЛП: раскройная задача.
Имеется
![]() стандартных заготовок (доски, прутья,
листы стали и т.д.), которые подлежат
раскрою на детали для сборки готового
изделия. Задано
стандартных заготовок (доски, прутья,
листы стали и т.д.), которые подлежат
раскрою на детали для сборки готового
изделия. Задано
![]() вариантов,
вариантов,
![]() ,
технологий раскроя:
,
технологий раскроя:
![]() ,
–
количество видов деталей. Это означает,
что при
,
–
количество видов деталей. Это означает,
что при
![]() –ом
варианте раскроя получают
–ом
варианте раскроя получают
![]() шт. деталей первого вида,
шт. деталей первого вида,
![]() шт. деталей второго вида и т.д. Часть
компонент
шт. деталей второго вида и т.д. Часть
компонент
![]() могут быть равны нулю, то есть данные
детали при
-ом
варианте раскроя не получают.
могут быть равны нулю, то есть данные
детали при
-ом
варианте раскроя не получают.
Хотя каждая из деталей, необходимых для сборки готовых изделий в каком-либо варианте раскроя присутствует.
Из
получаемых деталей можно собрать
видов готовых изделий. Для каждого вида
готовых изделий известен набор деталей,
из которых собирается это изделие:
![]() и цена реализации каждого готового
изделия –
и цена реализации каждого готового
изделия –![]() .
Надо составить такой план раскроя
заготовок (буквально – план для
раскройного цеха) и такой план сборки
готовых изделий (план для сборочного
цеха), чтобы реализация изделий дала
максимум суммарной выручки.
.
Надо составить такой план раскроя
заготовок (буквально – план для
раскройного цеха) и такой план сборки
готовых изделий (план для сборочного
цеха), чтобы реализация изделий дала
максимум суммарной выручки.
Модель:
Обозначим
![]() – число заготовок, раскраиваемых по
-й
технологии;
– число заготовок, раскраиваемых по
-й
технологии;
![]() –
число готовых изделий
-го
вида в плане выпуска сборочного цеха.
–
число готовых изделий
-го
вида в плане выпуска сборочного цеха.
Тогда:
![]() – план раскройного цеха,
– план раскройного цеха,
![]() – план сборочного цеха.
– план сборочного цеха.
![]() (2)
(2)
![]() – балансы
по деталям
– балансы
по деталям
![]() – баланс
по заготовкам
– баланс
по заготовкам
![]()
![]()
22.Частные задачи ЛП: станочная задача.
Станочная задача
Постановка задачи:
Имеется
типов станков,
(любое оборудование). Известен фонд
рабочего времени каждого типа станков
![]() ,
,
станко-часах за определенный промежуток
времени (сутки, квартал). На станках надо
изготовить детали, из которых собирается
готовое изделие одного
типа. Задан
набор деталей, из которых надо изготовить
одно готовое изделие:
,
,
станко-часах за определенный промежуток
времени (сутки, квартал). На станках надо
изготовить детали, из которых собирается
готовое изделие одного
типа. Задан
набор деталей, из которых надо изготовить
одно готовое изделие:
![]() .
То есть на сборку идет
штук деталей первого вида,
.
То есть на сборку идет
штук деталей первого вида,
![]() штук деталей второго вида и т.д. Каждую
деталь можно изготовить на станках
любого типа, но производительность их
на разных деталях разная.
штук деталей второго вида и т.д. Каждую
деталь можно изготовить на станках
любого типа, но производительность их
на разных деталях разная.
Известны
затраты
![]() времени в станко-часах на изготовление
одной детали
-го
вида на станке
-го
типа.
времени в станко-часах на изготовление
одной детали
-го
вида на станке
-го
типа.
Надо так распределить детали по станкам, чтобы за данный промежуток времени получить максимальное количество готовых изделий из произведенных деталей.
Модель:
Обозначим
![]() – количество деталей
-го
вида, которые должны изготавливаться
на станке
-го
типа;
–
число готовых изделий.
– количество деталей
-го
вида, которые должны изготавливаться
на станке
-го
типа;
–
число готовых изделий.
Тогда:
![]() – план производства деталей,
– план производства деталей,
![]() – план производства готовых изделий.
– план производства готовых изделий.
![]() (3)
(3)
![]() – балансы
по деталям,
– балансы
по деталям,
![]() – балансы
по фонду рабочего времени станков,
– балансы
по фонду рабочего времени станков,
![]() ,
,
![]()
23.Частные задачи ЛП: задача об использовании агрегатов.
Это модификация станочной задачи.
Типовая постановка задачи:
Имеется
типов машин,
,
в количествах
.
Из этих машин составляются агрегаты
типов,
![]() ,
для производства
видов,
,
работ в объемах
,
для производства
видов,
,
работ в объемах
![]() .
.
Для каждого -го агрегата известны:
![]() – число
машин
-го
типа, входящих в
-ый
агрегат,
– число
машин
-го
типа, входящих в
-ый
агрегат,
![]() – производительность
-го
агрегата на
-ом
виде работ,
– производительность
-го
агрегата на
-ом
виде работ,
![]() – стоимость
выполнения единицы
-го
вида работ агрегатом.
– стоимость
выполнения единицы
-го
вида работ агрегатом.
Надо выбрать такие варианты агрегатов и так распределить их по работам, чтобы при имеющейся технике выполнить требуемые объемы работ с минимальными затратами.
Модель:
Обозначим:
![]() – число комплектуемых агрегатов
-го
вида,
– число комплектуемых агрегатов
-го
вида,
![]() – число
-х
агрегатов, которые будут выполнять
-й
вид работ .
– число
-х
агрегатов, которые будут выполнять
-й
вид работ .
![]() (4)
(4)
![]() – балансы
по машинам при комплектовании агрегатов,
– балансы
по машинам при комплектовании агрегатов,
![]() – балансы
по агрегатам при их использовании,
– балансы
по агрегатам при их использовании,
![]() – балансы
по работам,
– балансы
по работам,
![]()
24.Задача минимизации времени выполнения всей программы работ.
Пусть
как в задаче (5), надо выполнить
видов работ в объемах
![]() ,
.
Известно количество оборудования
каждого типа
,
.
Известно количество оборудования
каждого типа
![]() ,
.
Каждая работа может выполняться на
каждом типе оборудования.
,
.
Каждая работа может выполняться на
каждом типе оборудования.
Задана
производительность оборудования
![]() ,
как затраты
времени на
выполнение
-ой
работы на
-ом
оборудовании. Тогда производственные
мощности должны быть выражены в расчете
на фиксированный промежуток времени
,
как затраты
времени на
выполнение
-ой
работы на
-ом
оборудовании. Тогда производственные
мощности должны быть выражены в расчете
на фиксированный промежуток времени
![]() ,
[час, сутки, квартал и т.д.]:
,
[час, сутки, квартал и т.д.]:
![]() .
.
Не будем фиксировать время выполнения всей программы работ – , сделав его искомой величиной. Необходимо так распределить работы по типам оборудования, чтобы всю программу работ выполнить на имеющемся оборудовании за минимальное время – .
Модель:
![]()
при условиях:
![]()
![]() (6)
(6)
![]()
Преобразуем первую группу ограничений к виду:
![]() (7)
(7)
Каждая работа может выполняться на каждом типе оборудования, то есть имеет место полная взаимозаменяемость оборудования.
Поэтому очевидно, что минимальное время достигается при строгих равенствах (7). Если хотя бы в одном из ограничений (7) левая часть меньше , то соответствующую мощность можно доиспользовать так, чтобы уменьшить общее время выполнения работ .
Перепишем (6) в виде:
при условиях:
![]() (8)
(8)
![]()
Задача (8) имеет специальный алгоритм численной реализации.
25.Распределительная задача линейного программирования.
РЗЛП – представляет собой специальную задачу линейного программирования транспортного типа, имеющую многочисленные приложения к задачам планирования, управления и проектирования.
