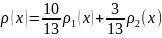- •. Моделирование случайных дискретных событий.
- •2. Ответ (X)
- •3. «Выбор купонов»
- •I,box:cardinal;
- •3. В театре
- •3. Короткий кусок стержня.
- •Поправки к приближенным распределениям.
- •3. При бросании 100 монет какова вероятность выпадения ровно 50 гербов
- •Разделение области моделирования случайной величины.
- •3. Задача Сэмуэля Пепайса
- •Общая характеристика методов.
- •Метод Неймана.
- •Моделирование усеченных распределений.
- •Выбор равномерно распределенных точек в сложных пространственных областях.
- •3 Длина хорды
Билет 8
. Моделирование случайных дискретных событий.
Рассмотрим дискретную случайную величину с распределением
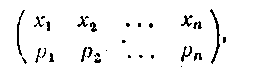 (1)
(1)
г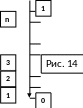 де
pi
=
P{
=
xi}.
Для того чтобы вычислить значения
этой величины разделим интервал
0
у < 1
на интервалы i
такие
(рис. 14), что длина i
фавна рi
.
де
pi
=
P{
=
xi}.
Для того чтобы вычислить значения
этой величины разделим интервал
0
у < 1
на интервалы i
такие
(рис. 14), что длина i
фавна рi
.
Т е о р е м а 1. Случайная величина , определенная формулой
= xi, когда i , (2)
имеет распределение вероятностей (1).
Доказательство занимает одну строку:
P{ = xi} =Р{i } = длина i = рi.
Для практической реализации формулы (2) удобно в накопителе ЭВМ расположить подряд значения х1, x2, ..., xn и p1, p1+p2, p1+p2+p3, ..., 1. Для того чтобы вычислить очередное значение , находим очередное . Затем сравниваем с p1. Если < p1, то = x1; если p1, то сравниваем с p1+p2. Если < p1+p2, то = x2; если p1+p2, то сравниваем с p1+p2+p3, и т.д.
Оптимизация метода интервалов.
Легко видеть, что в случае, когда = xi (1 i n-1), приходится осуществить i сравнений, и лишь в случае, когда = xn , число сравнений равно n–1. Поэтому среднее число сравнений, затрачиваемых при получении одного значения , равно
n–1
t = ipi + (n – 1)pn.
i=1
Так как порядок значений x1, ..., хп в (1) произволен, то выгодно расположить их в порядке убывания вероятностей, т. е. так, чтобы p1 p2 ... pn. Тогда величина t будет минимальной.
Расчет по формуле (2) заметно упрощается в случае, когда все значения x1,..., хп равновероятны: p1 = ... = pn = 1/n. В этом случае многократные сравнения не нужны: так как i – это интервал (i–1)/n < i/n, то условие i
равносильно условию i–1 n < i, или Ц(n) = i – 1. Вместо формулы (2) можно записать, что
= xi, где i = 1+ Ц(n).
Теорему 1 легко обобщить на случайную величину, которая может принимать бесконечную последовательность значений х1, x2, ..., xn, ... и имеет распределение
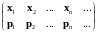 .
.
В этом случае числа хп и рn задаются формулами, и вычисление их при каждом расчете может оказаться весьма трудоемким. Тогда можно выбрать число n0 так, чтобы сумма вероятностей p1+...+pn0 была достаточно близкой к 1, и значения х1, ..., xn0 и p1, ..., pn0 заготовить заранее. Вычислять хi и рi по формулам придется только при i > n0, а это будет достаточно редко.
2. Ответ (X)
3. «Выбор купонов»
procedure TForm1.Button6Click(Sender: TObject); //выбор купонов
var
I,box:cardinal;
otvet:extended;
begin
otvet:=0;
i:=1;
N:=StrToInt(Form1.LabeledEdit1.Text);
// count:=0;
while (i<=N)do
begin
box:=1;// perviu vityanyli
while (true) do
begin
if random<=4/5 then
begin
box:=box+1;
break;
end
else box:=box+1;
end;
while (true) do
begin
if random<=3/5 then
begin
box:=box+1;
break;
end
else box:=box+1;
end;
while (true) do
begin
if random<2/5 then
begin
box:=box+1;
break;
end
else box:=box+1;
end;
while (true) do
begin
if random<=1/5 then
begin
box:=box+1;
break;
end
else box:=box+1;
end;
otvet:=otvet+box;
i:=i+1;
end;
otvet:=otvet/N;
Form1.Edit1.Text:=FloatToStr(otvet);
end;
Билет 9
Моделирование случайных непрерывных величин. Предположим, что случайная величина определена в интервале а<х<b и имеет плотность р(x)>0 при а<х<b. Обозначим через F(x) функцию распределения , которая при а < х < b равна
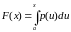
Случай a = – и (или) b = не исключается.
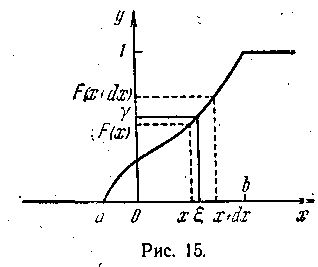
В тех случаях, когда уравнение F() = (4) аналитически разрешимо относительно , получается явная формула = G() для разыгрывания случайной величины , где G(y) – обратная функция по отношению к y = F(x). В других случаях можно уравнение (4) решать численно. Если объем накопителя позволяет, то удобно составить таблицу функции G(y), 0<y<1, и по ней находить значения . Иногда удобно использовать таблицу функции F(x), а < x < b, и находить значения обратной интерполяцией.
П р и м е р. Экспоненциальная случайная величина определена при x0 < x < с плотностью
p(x) = a e – a ( x – x0 ) .
Так
как 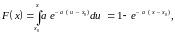 то
уравнение (4) принимает вид
то
уравнение (4) принимает вид
1 – e – a ( – x0 ) = .
Отсюда получаем явное выражение для расчета : = x0 – (1/а)1n(1– ). (5)
2.