§ 2. Підпростори лінійного простору.

1. Означення та приклади. Підмножина векторів лінійного простору називається лінійним підпростором простору , якщо вона замкнена відносно визначених в просторі лінійних операцій, тобто для неї справджується умова

. (13)

В кожний лінійний підпростір простору входить нульовий вектор простору . Справді, за умовою (13), разом з кожним вектором у підпросторі лежить вектор , тобто протилежний вектор. За тою самою умовою, в лежить і їх сума . Всі решта аксіоми лінійного простору для підпростору як підмножини векторів простору виконуються очевидним чином. Тому можна сказати, що підмножина сама є лінійним простором відносно визначених у просторі лінійних операцій.

Оскільки підпростір є лінійним простором, то такі поняття як вимірність, базис і т.п. властиві і для підпростору. Зазначимо, що вимірність підпростору не може перевищувати вимірності простору, бо в підпросторі не може бути ширшої системи лінійно незалежних векторів, ніж у самому просторі.

Нехай і – який-небудь базис підпростору . Доповнимо цей базис векторами до базису простору , . Величина називається ковимірністю підпростору і позначається , так що , а система векторів називається кобазисом підпростору .

Приклади.

1. У попередньому параграфі було показано, що сукупність многочленів, степінь яких не перевищує , утворює – вимірний простір. Оскільки кожний многочлен є неперервною на проміжку функцією, то вказана сукупність многочленів є – вимірним підпростором простору неперервних на проміжку функцій.

2. Нехай – який-небудь ненульовий вектор – вимірного лінійного простору . Згідно з (13), сукупність векторів , де пробігає відповідне числове поле, утворює одновимірний лінійний підпростір простору . Якщо до кожного з векторів додати один і той самий вектор , то отримаємо сукупність векторів

. (14)

У випадку тривимірного лінійного простору ми називали рівність (14) векторно-параметричним рівнянням прямої. За аналогією з тривимірним простором, сукупність векторів (14) у будь-якому лінійному просторі логічно називати прямою в цьому просторі. Сукупність векторів (14) не є, взагалі кажучи, лінійним підпростором. Одновимірний лінійний підпростір відрізняється від прямої (14) лише тим, що визначає пряму, яка проходить через початок координат паралельно до прямої (14).

Якщо у деякому базисі лінійного простору вектори мають відповідно координати , , , то векторна рівність (14) рівносильна системі скалярних рівностей

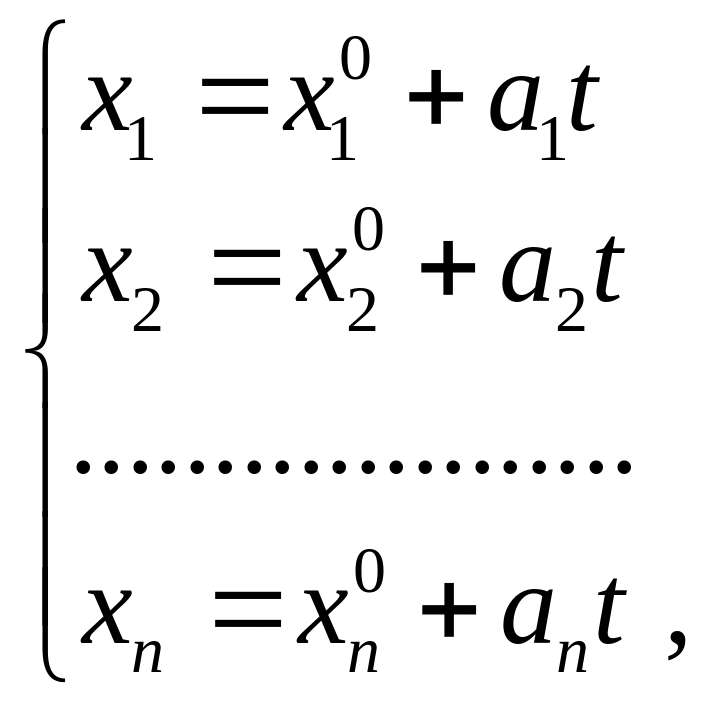(14′)

які називаються параметричними рівняннями прямої. З системи (14′) очевидним чином отримуються канонічні рівняння прямої:

.

3. Як і у попередньому прикладі, сукупність векторів лінійного простору , які мають вигляд , де , – зафіксовані лінійно незалежні вектори простору , а і пробігають незалежно один від одного все числове поле, утворюють двовимірний лінійний підпростір. Сукупність векторів

,

де – який-небудь зафіксований вектор, називається двовимірною площиною, яка, взагалі кажучи, не є лінійним підпростором.

Вправа. Записати параметричні рівняння двовимірної площини в – вимірному лінійному просторі .

2. Лінійні оболонки. В цьому пункті розглянемо один спосіб побудови лінійних підпросторів, який є узагальненням прикладів попереднього пункту.

Нехай – деяка система векторів лінійного простору . Позначимо через множину всеможливих лінійних комбінацій векторів . Сукупність є лінійним підпростором лінійного простору . Справді, якщо , тобто , , то і тому . Лінійний підпростір називається лінійною оболонкою векторів , або підпростором, натягненим на вектори , або підпростором, породженим системою векторів . Оскільки кожний вектор лінійної оболонки є лінійною комбінацією векторів , то за лемою про лінійні комбінації .

Підпростір , породжений лінійно незалежними векторами , є –вимірним лінійним підпростором простору , а вектори утворюють в ньому базис. Справді, оскільки кожний вектор лінійного підпростору можна подати як лінійну комбінацію лінійно незалежних векторів , то, за наслідком з леми про лінійні комбінації, ; при цьому система векторів є одним з можливих базисів лінійної оболонки . Таким чином, для кожного натурального , , в – вимірному лінійному просторі існує – вимірний лінійний підпростір. Таким підпростором є лінійна оболонка будь-яких лінійно незалежних векторів. Зокрема, сам лінійний простір є лінійною оболонкою будь-якого свого базису. Зазначимо, що для справджується умова (13), тому є лінійним підпростором, до того ж .

За означенням, лінійна оболонка лінійно незалежних векторів простору збігається з множиною всеможливих лінійних комбінацій , де числа пробігають незалежно одне від одного всю числову множину. За аналогією з тривимірним простором, сукупність векторів

,

де – деякий зафіксований вектор, називається – площиною лінійного простору , або –вимірним лінійним многовидом. Якщо в деякому базисі – вимірного простору , , , , то з останньої векторної рівності отримуємо параметричні рівняння – площини:

3. Гіперплощини. Виберемо в – вимірному лінійному просторі який-небудь базис і позначимо через сукупність векторів лінійного простору координати яких у вибраному базисі задовольняють лінійне рівняння

, (15)

де – набір сталих, серед яких принаймні одна, наприклад , не дорівнює нулеві. Покажемо, що сукупність є лінійним підпростором. Очевидно, що нуль-вектор належить . Далі, нехай вектори , належать сукупності , тобто для цих векторів справджуються рівності

(16)

Координати лінійної комбінації , на підставі (16), задовольняють рівняння (15):

,

тобто , а це означає, що – лінійний підпростір.

Покажемо тепер, що і знайдемо базис . Звичайною перевіркою переконуємося, що кожен з векторів системи

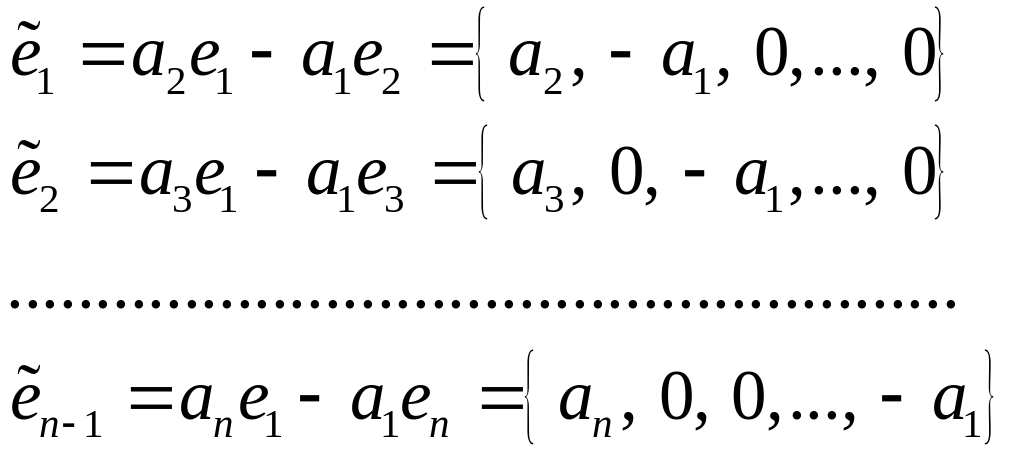(17)

належить підпросторові . Покажемо, що вектори (17) лінійно незалежні. Припустимо супротивне і нехай існують такі числа , що

.

Перейшовши до покоординатного запису, дістаємо систему рівностей:

За умовою , тому , що й означає, що система векторів (17) лінійно незалежна.

Покажемо тепер, що будь-який вектор лінійного підпростору , можна єдиним чином розкласти за векторами . Якщо це можливо, то повинен існувати єдиний набір чисел , що

, (18)

або, в координатному записі,

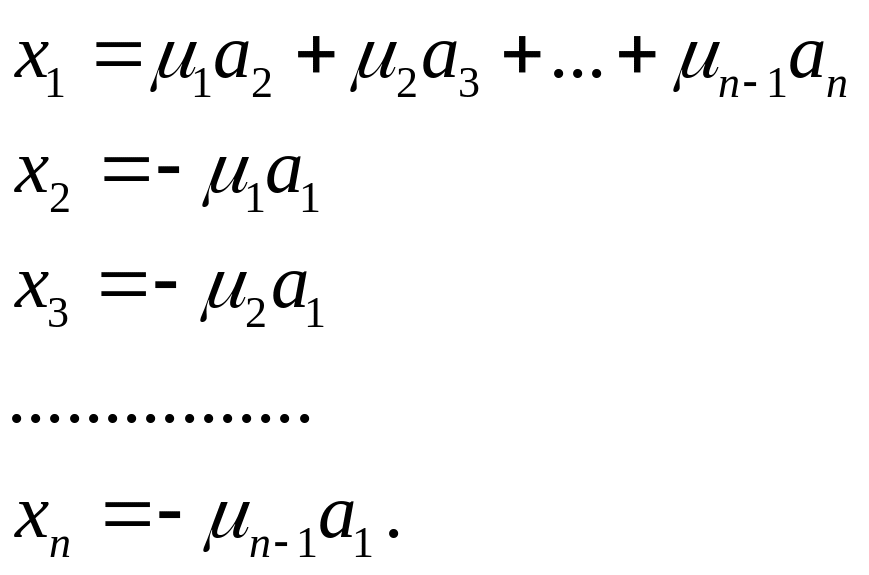
Звідси, , , тобто коефіцієнти лінійної комбінації (18) однозначно визначаються вектором , а перша рівність останньої системи перетворюється у рівняння (15). На підставі наслідку з леми про лінійні комбінації . Звідси, система векторів є базисом підпростору .

Розглянемо сукупність векторів лінійного простору , де , , а ─ який-небудь зафіксований вектор простору . Тоді . Підставивши координати вектора в рівняння (15) і позначивши , отримаємо рівняння

. (19)

Сукупність векторів лінійного простору, кожен з яких задовольняє рівняння (19), називається гіперплощиною даного лінійного простору. Звідси, рівняння (15) визначає гіперплощину, яка проходить через початок координат. Зазначимо, що поняття гіперплощини збігається з поняттям – площини при .

4. Перетин та сума лінійних підпросторів. Перетином двох лінійних підпросторів та лінійного простору називається сукупність векторів, яка належить кожному з підпросторів , і позначається символом .

Легко показати, що перетин є лінійним підпростором лінійного простору . Справді, кожному з підпросторів , належить нульовий вектор простору , тому нульовий вектор належить перетинові , тобто – непорожня множина. Далі, якщо деякі вектори належать перетинові , то вони, а разом з ними і їх всеможливі лінійні комбінації , належать кожному з підпросторів та , тому належать .

Приклад. Якщо , – два двовимірні лінійні підпростори тривимірного простору (дві площини, що проходять через початок координат), то – одновимірний лінійний підпростір (пряма перетину цих площин).

Сумою двох підпросторів , лінійного простору називається сукупність всеможливих векторів , які можна подати у вигляді

, , . (20)

Сума підпросторів і позначається символом .

Покажемо, що сума двох лінійних підпросторів є лінійним підпростором. Очевидно, що нуль-вектор простору входить в . Нехай – два вектори сукупності . Тоді , , де , . Звідси, . Оскільки , , то .

Приклад. Нехай , – два двовимірні лінійні підпростори тривимірного лінійного простору, . Тоді сума збігається з самим тривимірним простором.

Зауваження. Слід пам’ятати, що в означенні суми двох лінійних підпросторів не вимагається, щоб вектор підпростору можна було подати єдиним способом у вигляді суми двох векторів – один з простору , а другий з простору .

Виберемо в базис . Доповнимо цей базис, з одного боку, до базису , підпростору , а з другого боку, – до базису , підпростору .

Теорема про базис суми лінійних підпросторів. Система векторів , , є базисом суми лінійних підпросторів та .

Доведення. Покажемо спочатку, що ця система векторів лінійно незалежна. Припустимо супротивне і нехай

, (22)

або

.

Ліва частина цієї рівності є вектором підпростору , а права – підпростору . Рівність цих двох векторів означає, що права частина належить і підпростору , тому , а тому цей вектор можна розкласти за базисом :

,

або

.

Але вектори , утворюють базис підпростору , тобто вони лінійно незалежні, тому, зокрема, . Тоді (22) набуває вигляду

.

Оскільки , – базис простору , то , тобто система векторів , , лінійно незалежна.

Покажемо тепер, що будь-який вектор можна розкласти за векторами цієї системи. За означенням суми двох підпросторів будь-який вектор можна подати у вигляді суми

, , .

Вектор можна розкласти за векторами базису , простору , а вектор можна розкласти за векторами базису , простору . Сумуючи обидва розклади, дістаємо, що вектор є лінійною комбінацією векторів , , . За наслідком з леми про лінійні комбінації , тому система векторів , , є базисом підпростору . Теорему доведено.

Теорема про вимірності. Нехай , – два лінійні підпростори лінійного простору . Тоді

. (23)

Доведення. Як і у попередній теоремі, виберемо в базис і доповнимо його до базису , підпростору , а також до базису , підпростору . За теоремою про базис суми, . Оскільки базис простору складається з векторів , , то . Точно так само , . Звідси,

.

Приклад. Перетин двох різних гіперплощин , , – вимірного лінійного простору , які проходять через початок координат, є – вимірним лінійним підпростором простору . Справді, враховуючи, що , з рівності (21) маємо . Звідси, .

5. Прямі суми лінійних підпросторів. Якщо два лінійні підпростори , лінійного простору перетинаються лише по нульовому вектору цього простору, , то сума називається прямою сумою цих підпросторів.

Пряму суму будемо позначати . З теореми про вимірності .

Приклад. Нехай базисом тривимірного лінійного простору є трійка некомпланарних векторів , , . Позначимо через лінійну оболонку (координатна площина ), через – лінійну оболонку (координатна площина ), а через – одновимірний лінійний підпростір з базисним вектором (координатна вісь ). Тоді збігається з , але ця сума не є прямою; сума також збігається з і є прямою сумою.

Теорема. Сума двох лінійних підпросторів , лінійного простору є прямою сумою тоді і лише тоді, коли кожний вектор можна єдиним способом подати у вигляді суми , , .

Доведення. Нехай сума є прямою сумою і припустимо, що деякий вектор можна подати у вигляді суми двома способами – , , , . Прирівняємо праві частини цих рівностей, , і перепишемо отриману рівність так:

.

Ліва частина визначає вектор підпростору , а права – підпростору , тому , . Позаяк , то , . Звідси, остаточно, , , тобто вектор можна подати у вигляді суми , , єдиним чином.

Навпаки, нехай кожний вектор можна подати у вигляді суми , , єдиним способом і припустимо, що сума не є прямою, тобто . Тоді, якщо – базис , , – базис , а , – базис , то, за теоремою про базис суми лінійних підпросторів, система векторів , , є базисом простору . Розкладемо вектор за векторами базису:

Позначимо , , . Тоді , , , але , . Суперечність. Теорему доведено.