Теорема Котельникова-Шеннона

Напомним определения понятий дискретизации и интерполяции. Определение: Представление непрерывного (аналогового) сигнала x(t) дискретной последовательностью отсчетов x(tk)=x(k t ∆ ) , по которым с заданной точностью можно восстановить исходный непрерывный сигнал , называется дискретизацией на равномерной сетке. Определение: Процесс восстановления дискретизированного сигнала называется интерполяцией. Допустим , у нас есть непрерывное изображение i(x,y) . После дискретизации мы получаем дискретное изображение I(xk,ym) . Затем интерполируем его и переходим к изображению i’(x,y). Естественно возникает вопрос :

Как нужно проводить дискретизацию, чтобы не происходила потеря информации, т.е. при каких условиях исходное изображение i(x,y) совпадает с восстановленным i’(x,y)?

Ответ на этот вопрос может быть получен из теоремы Котельникова-Шеннона.

Теорема Котельникова-Шеннона.

Напомним определения пространств L1 и L2 и норм в них. Определение. Пространством L1(R) называется пространство комплекснозначных или действительных функций , интегрируемых на множестве R. Определение. Нормой элемента f в пространстве L1(R) называется величина

Определение. Пространством L2(R) называется пространство комплекснозначных или действительных функций интегрируемых на множестве R с квадратом. L2(R) – евклидово пространство, скалярное произведение для элементов f и g в нем вводится как Определение. Нормой элемента f в пространстве L2(R) называется величина

Преобразование Фурье F( γ ) функции f(t) определяется как

для всех ∈ γ R. Обозначим через A(R) множество преобразований Фурье всех функций f, принадлежащих пространству L1(R). Теорема. Пусть f∈L1(R) ∩ A(R) или f ∈L2(R). Предположим, даны константы T, Ω >0 такие что

F(γ ) равна 0 вне сегмента [-ω,ω] (1)

и

0<2TΩ ≤1. (2)

Тогда

(3)

причем ряд сходится поточечно на R, если f ) R ( A ) R ( L1 ∩ ∈ , и ряд сходится равномерно, если f ) R ( L2 ∈ .

Т.о., сигнал, описываемый непрерывной функцией времени f(t) с ограниченным спектром, полностью определяется своими значениями, отсчитанными через интервалы времени T=1/(2Ω), где Ω- ширина спектра сигнала. Доказательство: 1) Пусть f ) R ( A ) R ( L1 ∩ ∈ . Введем функцию G( γ)

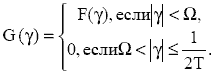
Продолжим ее периодически с периодом 1/T на R. Тогда можем разложить G( γ ) в ряд Фурье, имеющий вид:

где

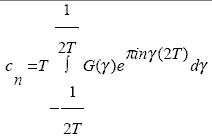
Из определения функции G( γ ) и из формулы обращения следует, что . -<по формуле обращения> -<по определению функции G( γ )> -<подставили выражение для ряда Фурье функции G( γ)> -<ряды Фурье интегрируемых функций можно интегрировать почленно> -<получаем простым интегрированием> -<т.к. cn=Tf(nT), умножили и поделили на 2Ω> , ч.т.д. 2) Пусть f ∈L2(R). В пространстве L2 теорема доказывается аналогично. Так же вводим функцию G( γ ), периодически продолжаем ее на R и раскладываем в ряд Фурье. Заметим, что по определению преобразования Фурье в L2

(5)

Пусть Sn( γ )-n-я частичная сумма ряда Фурье функции G( γ ). Введем функцию . Тогда ,

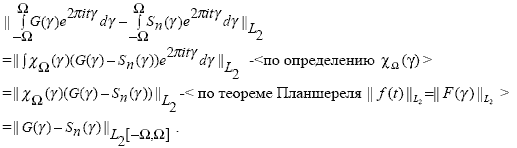(6)

Так как Sn-n-я частичная сумма ряда Фурье G, то Используя это соотношение, (5) и (6), а также неравенство Гельдера и определение коэффициентов "Сn", получаем требуемое в теореме равенство. Теорема доказана.

Замечания к теореме Котельникова-Шеннона .

Замечание 1. Основой доказательств теоремы в пространствах L1 и L2 является возможность перехода от преобразования Фурье к рядам Фурье. Замечание 2. Исследуем вопрос о том, можно ли ослабить условие (2) теоремы. Приведенный ниже пример показывает, что этого сделать нельзя.

Допустим, константы T, Ω >0 удовлетворяют неравенству 2TΩ>1.

Возьмем функцию 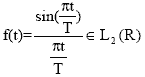Ясно, что преобразование Фурье этой функции Следовательно, условие (1) выполнено. Так как , то правая часть формулы (3) Функции f и g не равны, так как обе непрерывны на R и f(0)=1, а g(0)=2TΩ>1. Т.е. правая часть не равна левой части, что противоречит условию, следовательно предположение о том, что 2TΩ>1 не верно. Итак, мы доказали, что, если функция f разложима в ряд Котельникова (3) и спектр ее равен нулю вне отрезка [-Ω,Ω], выполняется соотношение 0<2TΩ ≤1. Замечание 3. В формуле (3) константу T обычно называют периодом дискретизации, последовательность {f(nT) : n∈Z} –последовательностью дискретизированных значений. Частота 2Ω называется частотой Найквеста или частотой дискретизации. Это минимальная частота, с которой нужно посылать импульсы, чтобы не было потери информации. T≡ 1/2Ω - масксимальный период дискретизации, т.е. максимальный приемлемый промежуток времени между передаваемыми импульсами. Замечание 4. На практике восстановленная функция f0(t), как правило, не совпадает точно передаваемой функцией f(t). Ошибка обусловлена, например, тем, что спектр передаваемой функции f(t) обычно ограничен не резко. Это вытекает хотя бы из того факта, что все реальные сигналы ограничены во времени и , следовательно, имеют неограниченные строго спектры. Выбор интервалов отсчетов T>0 означает, что все спектральные составляющие спектра с частотами T max π = Ω > ω не передаются и не могут быть восстановлены. Если 2TΩ>1, то исходная функция не может быть восстановлена, возникающий эффект

Параллельные АЦП

    АЦП этого типа осуществляют квантование сигнала одновременно с помощью набора компараторов, включенных параллельно источнику входного сигнала. На рис. 3 показана реализация параллельного метода АЦ-преобразования для 3-разрядного числа.

    С помощью трех двоичных разрядов можно представить восемь различных чисел, включая нуль. Необходимо, следовательно, семь компараторов. Семь соответствующих эквидистантных опорных напряжений образуются с помощью резистивного делителя.

    Если приложенное входное напряжение не выходит за пределы диапазона от ⁵/₂h, до ⁷/₂h, где h=U_оп/7 - квант входного напряжения, соответствующий единице младшего разряда АЦП, то компараторы с 1-го по 3-й устанавливаются в состояние 1, а компараторы с 4-го по 7-й - в состояние 0. Преобразование этой группы кодов в трехзначное двоичное число выполняет логическое устройство, называемое приоритетным шифратором, диаграмма состояний которого приведена в табл.1.

Таблица 1

Входное напряжение	Состояние компараторов							Выходы
Uвх/h	К7	К6	К5	К4	К3	К2	К1		Q2	Q1	Q0
0 1 2 3 4 5 6 7	0 0 0 0 0 0 0 1	0 0 0 0 0 0 1 1	0 0 0 0 0 1 1 1	0 0 0 0 1 1 1 1	0 0 0 1 1 1 1 1	0 0 1 1 1 1 1 1	0 1 1 1 1 1 1 1		0 0 0 0 1 1 1 1	0 0 1 1 0 0 1 1	0 1 0 1 0 1 0 1

    Подключение приоритетного шифратора непосредственно к выходу АЦП может привести к ошибочному результату при считывании выходного кода. Рассмотрим, например переход от трех к четырем, или в двоичном коде от 011 к 100. Если старший разряд вследствие меньшего времени задержки изменит свое состояние раньше других разрядов, то временно на выходе возникнет число 111, т.е. семь. Величина ошибки в этом случае составит половину измеряемого диапазона.

    Так как результаты АЦ-преобразования записываются, как правило, в запоминающее устройство, существует вероятность получить полностью неверную величину. Решить эту проблему можно, например, с помощью устройства выборки-хранения (УВХ). Некоторые интегральные микросхемы (ИМС) параллельных АЦП, например МАХ100, снабжаются сверхскоростными УВХ, имеющими время выборки порядка 0,1 нс. Другой путь состоит в использовании кода Грея, характерной особенностью которого является изменение только одной кодовой позиции при переходе от одного кодового значения к другому. Наконец, в некоторых АЦП (например, МАХ1151) для снижения вероятности сбоев при параллельном АЦ-преобразовании используется двухтактный цикл, когда сначала состояния выходов компараторов фиксируются, а затем, после установления состояния приоритетного шифратора, подачей активного фронта на синхровход выходного регистра в него записывают выходное слово АЦП.

    Как видно из табл. 1, при увеличении входного сигнала компараторы устанавливаются в состояние 1 по очереди - снизу вверх. Такая очередность не гарантируется при быстром нарастании входного сигнала, так как из-за различия во временах задержки компараторы могут переключаться в другом порядке. Приоритетное кодирование позволяет избежать ошибки, возможной в этом случае, благодаря тому, что единицы в младших разрядах не принимаются во внимание приоритетным шифратором.

    Благодаря одновременной работе компараторов параллельный АЦП является самым быстрым. Например, восьмиразрядный преобразователь типа МАХ104 позволяет получить 1 млрд отсчетов в секунду при времени задержки прохождения сигнала не более 1,2 нс. Недостатком этой схемы является высокая сложность. Действительно, N-разрядный параллельный АЦП сдержит 2^N-1 компараторов и 2^N согласованных резисторов. Следствием этого является высокая стоимость (сотни долларов США) и значительная потребляемая мощность. Тот же МАХ104, например, потребляет около 4 Вт.

АЦП последовательного приближения

Преобразователь этого типа, называемый в литературе также АЦП с поразрядным уравновешиванием, является наиболее распространенным вариантом последовательных АЦП.

В основе работы этого класса преобразователей лежит принцип дихотомии, т.е последовательного сравнения измеряемой величины с ¹/₂, ¹/₄, ¹/₈ и т.д. от возможного максимального значения ее. Это позволяет для N-разрядного АЦП последовательного приближения выполнить весь процесс преобразования за N последовательных шагов (итераций) вместо 2^N-1 при использовании последовательного счета и получить существенный выигрыш в быстродействии. Так, уже при N=10 этот выигрыш достигает 100 раз и позволяет получить с помощью таких АЦП до 10⁵...10⁶ преобразований в секунду. В то же время статическая погрешность этого типа преобразователей, определяемая в основном используемым в нем ЦАП, может быть очень малой, что позволяет реализовать разрешающую способность до 18 двоичных разрядов при частоте выборок до 200 кГц (например, DSP101 фирмы Burr-Brown).

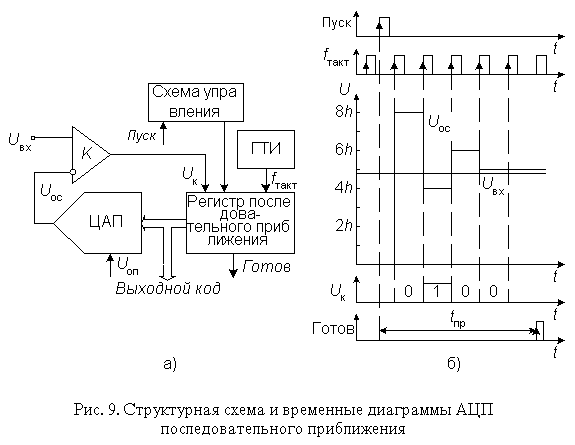
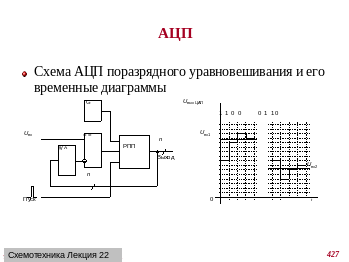
Рассмотрим принципы построения и работы АЦП последовательного приближения на примере классической структуры (рис. 9а) 4-разрядного преобразователя, состоящего из трех основных узлов: компаратора, регистра последовательного приближения (РПП) и ЦАП.

После подачи команды "Пуск" с приходом первого тактового импульса РПП принудительно задает на вход ЦАП код, равный половине его шкалы (для 4-разрядного ЦАП это 1000₂=8₁₀). Благодаря этому напряжение U_ос на выходе ЦАП (рис. 9б)

где h - квант выходного напряжения ЦАП, соответствующий единице младшего разряда (ЕМР). Эта величина составляет половину возможного диапазона преобразуемых сигналов. Если входное напряжение больше, чем эта величина, то на выходе компаратора устанавливается 1, если меньше, то 0. В этом последнем случае схема управления должна переключить старший разряд d₃ обратно в состояние нуля. Непосредственно вслед за этим остаток

таким же образом сравнивается с ближайшим младшим разрядом и т.д. После четырех подобных выравнивающих шагов в регистре последовательного приближения оказывается двоичное число, из которого после цифро-аналогового преобразования получается напряжение, соответствующее Uвх с точностью до 1 ЕМР. Выходное число может быть считано с РПП в виде параллельного двоичного кода по N линиям. Кроме того, в процессе преобразования на выходе компаратора, как это видно из рис. 9б, формируется выходное число в виде последовательного кода старшими разрядами вперед.

Быстродействие АЦП данного типа определяется суммой времени установления t_уст ЦАП до установившегося значения с погрешностью, не превышающей 0,5 ЕМР, времени переключения компаратора t_к и задержки распространения сигнала в регистре последовательного приближения t_з. Сумма t_к + t_з является величиной постоянной, а t_уст уменьшается с уменьшением веса разряда. Следовательно для определения младших разрядов может быть использована более высокая тактовая частота. При поразрядной вариации f_такт возможно уменьшение времени преобразования t_пр на 40%. Для этого в состав АЦП может быть включен контроллер.

При работе без устройства выборки-хранения апертурное время равно времени между началом и фактическим окончанием преобразования, которое так же, как и у АЦП последовательного счета, по сути зависит от входного сигнала, т.е. является переменным. Возникающие при этом апертурные погрешности носят также нелинейный характер. Поэтому для эффективного использования АЦП последовательного приближения, между его входом и источником преобразуемого сигнала следует включать УВХ. Большинство выпускаемых в настоящее время ИМС АЦП последовательного приближения (например, 12-разрядный МАХ191, 16-разрядный AD7882 и др.), имеет встроенные устройства выборки-хранения или, чаще, устройства слежения-хранения (track-hold), управляемые сигналом запуска АЦП. Устройство слежения-хранения отличается тем, что постоянно находится в режиме выборки, переходя в режим хранения только на время преобразования сигнала.

Данный класс АЦП занимает промежуточное положение по быстродействию, стоимости и разрешающей способности между последовательно-параллельными и интегрирующими АЦП и находит широкое применение в системах управления, контроля и цифровой обработки сигналов.

 

Аналого-цифровые преобразователи. Существуют три основных типа АЦП: интегрирующий, последовательного приближения и параллельный. Интегрирующий АЦП усредняет входной сигнал по времени. Из трех перечисленных типов это самый точный, хотя и самый «медленный». Время преобразования интегрирующего АЦП лежит в диапазоне от 0,001 до 50 с и более, погрешность составляет 0,1–0,0003%. Погрешность АЦП последовательного приближения несколько больше (0,4–0,002%), но зато время преобразования – от ~10мкс до ~1 мс. Параллельные АЦП – самые быстродействующие, но и наименее точные: их время преобразования порядка 0,25 нс, погрешность – от 0,4 до 2%.

Методы дискретизации. Сигнал дискретизируется по времени путем быстрого измерения его в отдельные моменты времени и удержания (сохранения) измеренных значений на время преобразования их в цифровую форму. Последовательность полученных дискретных значений может выводиться на дисплей в виде кривой, имеющей форму сигнала; возводя эти значения в квадрат и суммируя, можно вычислять среднеквадратическое значение сигнала; их можно использовать также для вычисления времени нарастания, максимального значения, среднего по времени, частотного спектра и т.д. Дискретизация по времени может производиться либо за один период сигнала («в реальном времени»), либо (с последовательной или произвольной выборкой) за ряд повторяющихся периодов.

АЦП многотактного интегрирования

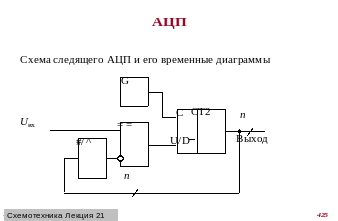
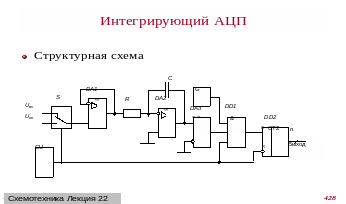
Структурная схема интегрирующего АЦП показана на рис. 8.7, а временная диаграмма его работы на рис. 8.8.

 

 

Рис. 8.7. Структурная схема интегрирующего АЦП

 

Этот АЦП использует метод двухтактного интегрирования. Входное напряжение интегрируется в течение фиксированного времени Т₁.  В конце интервала счетчик сбрасывается, а вход интегратора переключается на источник опорного сигнала. 

Выходное напряжение интегратора теперь уменьшается по линейному закону до нулевого значения, где счетчик останавливается и интегратор устанавливается в исходное состояние. Заряд, накопленный интегрирующим конденсатором в течение первого интервала, должен быть равен заряду, потерянному им в течение второго интервала.

 

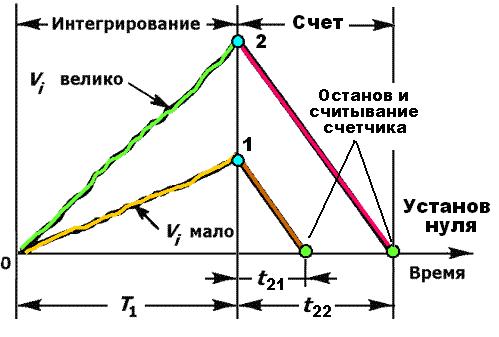
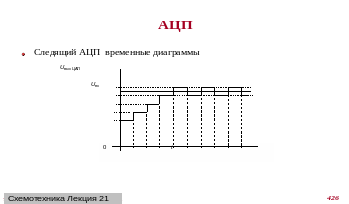
Рис. 8.8. Временная диаграмма его работы интегрирующего АЦП

 

Поэтому (8.1):

 

T₁Vi=t₂Vr

 

Отсюда (8.2):

 

 

 

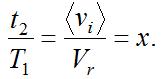
Отношение временных интервалов является одновременно отношением содержимого счетчика к числовому выражению полного диапазона счета.

Поэтому состояние счетчика в конце интервала t2 представляет собой выходное слово на двоичном выходе АЦП. Эта схема легко модифицируется для АЦП, использующих другие выходные коды. Этот метод АЦП обеспечивает компенсацию высокочастотных шумов при интегрировании и отличные шумовые характеристики, однако имеет невысокое быстродействие.

Статическая точность АЦП многотактного интегрирования определяется точностью источника опорного напряжения и смещением нуля интегратора и компаратора, которые суммируются с опорным напряжением. Смещение нуля можно устранить автоматической компенсацией. Для этого в цикл преобразования вводят дополнительную стадию и специальную схему установки нуля.

Интегральные АЦП многотактного интегрирования изготавливаются в виде:

– 12- и 18-разрядных схем с параллельным или последовательным выходом для сопряжения с микропроцессорами;

– схем с двоично-десятичными счетчиками и дешифраторами для управления семисегментными индикаторами, в том числе мультиплексированными.