2.3. Метод штрафных функций

В этом разделе будем исследовать функции нескольких переменных на наличие локального минимума методом, получившим название «метод штрафных функций».

Этим методом могут быть решены задачи, содержащие десятки ограничений типа «неравенства». Будем решать следующую задачу.

Для целевой функции

(2.35)

указать такой вектор , при котором достигает минимума, при этом должны выполняться ограничения:

(2.36)

(2.37)

В геометрической интерпретации эта задача формулируется так: среди точек области D, являющуюся пересечением областей и , найти такую точку, в которой функция достигает минимума.

Метод штрафных функций преобразует исходную задачу (2.35) – (2.37) на условный экстремум в задачу на безусловный экстремум. Задачу (2.35) – (2.37) решим сначала по частям.

Задача первая. Найти минимум функции

(2.38)

при ограничениях

, , m < n. (2.39)

Сформируем расширенную функцию

, (2.40)

где – некоторые большие положительные константы.

Величину назовем штрафом за невыполнение ограничения . Обратим внимание на тот факт, что штраф – функция неотрицательная, см. рис. 2.7.

Е сли – штраф для одного i-го ограничения, то – штраф за невыполнение всех ограничений. Численные значения констант назначаются так, чтобы имело место неравенство

. (2.41)

Очевидно, что для (2.40) возможен следующий минимум – , и . Этот исход эквивалентен задаче (2.38), (2.39).

Выясним, какую роль играет тот факт, что при любом x . При таком условии в большей мере будет минимизироваться штраф . В этом можно убедиться, если рассмотреть, например, градиент функции . Как следует из выражения (2.40),

.

При достаточно больших и тогда , т.е. практически будет минимизироваться только штраф . Следовательно, траектория поиска будет стремиться в первую очередь попасть в область (область, где выполнены все ограничения ).

Когда же в выражении доля штрафа и доля станут примерно равными (точнее, их градиенты), то примерно и в одинаковой пропорции будут минимизироваться штраф и .

Обозначим через точку, являющуюся решением поставленной задачи (2.38), (2.39), а через точку, в которой достигает минимума функция при некотором конкретном наборе коэффициентов (вектор ).

Показано [7], что при ( , ) . Это утверждение нужно понимать так, что если построить последовательность векторов … с неограниченно возрастающими компонентами, то соответствующая этим векторам последовательность точек должна сходиться к точке . Так и будем поступать.

Пример. Найти такие значения и , при которых целевая функция

(2.42)

достигает минимума, при этом необходимо, чтобы

. (2.43)

Геометрическая интерпретация этой задачи такова – среди точек окружности найти такую, в которой функция (2.42) достигает минимума, см. рис. 2.8.

Эту задачу можно решить и методом Лагранжа:

;

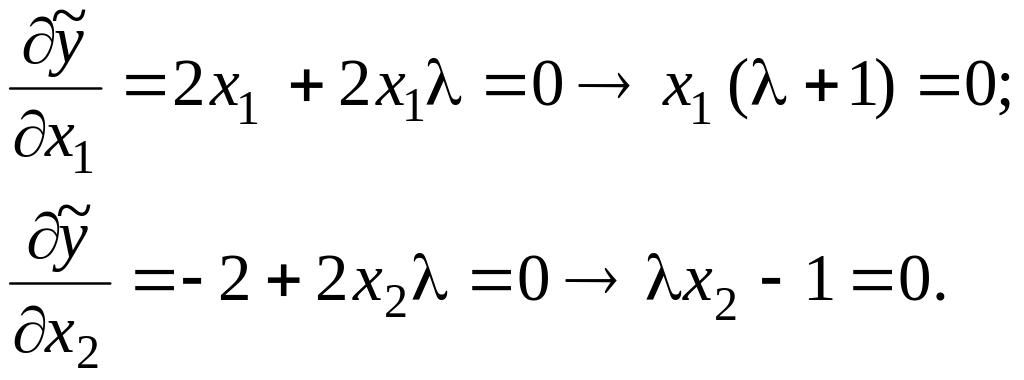(2.44)

Имеем три варианта решения системы (2.44):

а) ; (2.45)

б) ; (2.46)

в) . (2.47)

К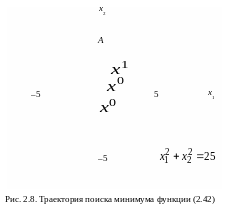 ак следует из (2.45) – (2.47), решением задачи (2.42), (2.43) является точка A, рис. 2.8. Ломаными линиями показаны примерные траектории поиска для различных исходных точек .

Получим теперь решение задачи (2.42), (2.43) методом штрафных функций. Согласно (2.38) – (2.40)

. (2.48)

Найдем минимум функции (2.48). Задачу эту можно решать различными методами – классическим, т.е. через необходимые и достаточные условия, градиентным методом и т.п.

Задача вторая. Найти минимум функции

(2.49)

при ограничениях

, . (2.50)

При решении этой задачи методом штрафных функций вспомогательная целевая функция формируется как

, (2.51)

г де – штраф за невыполнение ограничений (2.50).

Рассмотрим способы формирования функции .

а) «Бесконечный барьер». В этом случае штраф за невыполнение отдельного i-го ограничения принимает значение равное единице в тех точках, где (недопустимые точки) и нулевое значение в допустимых точках, т.е. где , рис. 2.9.

Другими словами,

(2.52)

Общий штраф оформляется как

,

где в качестве можно принять, например, число или любое другое большое число, обеспечивающее выполнение основного условия метода штрафных функций: .

Пусть – допустимая область, определяемая ограничениями (2.50). Тогда в рассматриваемом случае исходная точка может быть выбрана как внутри, так и вне допустимой области .

б) Сигнатурный штраф. Штраф будем формировать так, что

, (2.53)

где – большие положительные числа, а

(2.54)

Если , то . Допустим, что одно i-е ограничение нарушено, т.е. имеем (точка находится вне области ), тогда

, (2.55)

Поскольку , то , следовательно, в первую очередь минимизируется штраф , а это означает, что должна принимать положительные значения – точка x вернется в . Исходная точка может назначаться произвольно. Показано [7], что решение задачи (2.49), (2.50) рассматриваемым приемом может быть получено при , . Это условие следует понимать так, что задачу (2.49), (2.50) необходимо решать несколько раз, постоянно наращивая величины , . Можно рекомендовать, например, следующее правило, , где – номер приближения.

в) Метод внутренней точки. В этом случае

. (2.56)

Исходная точка должна принадлежать области . При приближении x к границе области штраф резко возрастает. Точка x начнет отходить от границы. Требования к R таковы – от итерации к итерации R должно убывать. Можно рекомендовать следующую закономерность

, (2.57)

где номер итерации.

Общий случай. Минимизировать

(2.58)

при ограничениях

, (2.59)

(2.60)

В этом случае

, (2.61)

где штраф за невыполнение ограничений (2.60) может назначаться одним из рассмотренных выше трех способов.

Пример. Пусть

; (2.62)

; (2.63)

;

. (2.64)

Область D, отвечающая ограничениям (2.63), (2.64), изображена на рис. 2.10.

Как легко установить, функция (2.62) при отсутствии ограничений достигает минимума в точке . Пусть далее известно, что решением задачи (2.62) – (2.64) является точка . Найдем теперь решение этой же задачи методом штрафных функций. Используя метод внутренней точки (2.56), запишем

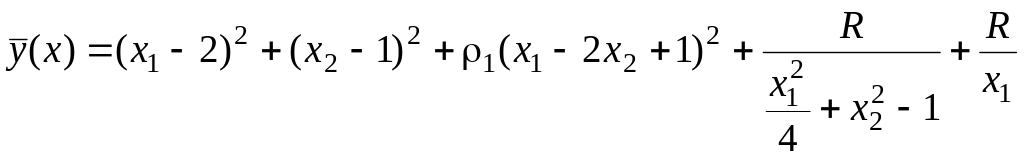
. (2.65)

Минимум функции (2.65) будем искать методом наискорейшего спуска, приняв следующую закономерность изменения весовой константы R от итерации к итерации

, (2.66)

Для примем

, . (2.67)

Подчеркнем, что в (2.66), (2.67) k – номер итерации по отысканию минимума функции (2.65). Так в первый раз отыскивается точка , при этом . Точка берется за начальную и вновь отыскивается минимум функции (2.65), но уже при и , находится точка и т.д. Примерный вид поисковой траектории для двух вариантов исходной точки показан на рис. 2.10. Читателю предлагается объяснить, почему именно такой вид имеют траектории.