1.3. Численные методы нахождения локального минимума функции одного переменного

Введение. В предыдущем разделе была решена задача отыскания локального минимума (максимума) дифференцируемой функции, причем дифференцируемой она должна быть, как минимум, дважды. Однако не всякая функция, имеющая локальный минимум, является дифференцируемой. Кроме того, нередки случаи, когда функция является дифференцируемой, однако выражения для ее производных являются настолько сложными и громоздкими, что использование их становится практически не оправданным. И в том и в другом случае при отыскании локального минимума можно применить численные методы. Ниже будут рассмотрены три таких метода. Все они применимы для исследования только так называемых унимодальных функций.

Унимодальной назовем такую функцию, которая имеет единственную точку локального минимума и функция эта монотонно убывает слева от точки и монотонно возрастает справа от .

Заметим, что может быть граничной точкой исследуемого интервала [a, b]. В таком случае функция должна быть монотонной в исследуемом интервале. Кроме того, подчеркнем, что унимодальная функция не обязана быть дифференцируемой. Мало того, она может иметь разрывы первого рода см. рис. 1.13.

Из определения унимодальной функции вытекает, что если назначить четыре точки так, что (рис. 1.14)

, (1.57)

то

. (1.58)

Из определения унимодальной функции вытекает следующее

Следствие. Допустим, что на интервале [a,b] задана унимодальная функция . Пусть и – некоторые такие две точки интервала , что . Допустим, что при этом

. (1.59)

П окажем, что в таком случае , т.е. (рис. 1.15), т.е. точка может находиться только справа от точки .

Допустим обратное, т.е. пусть при выполнении (1.59)

.

В таком случае точки и оказываются лежащими справа от точки минимума , следовательно, согласно свойству унимодальности должно иметь место неравенство

.

Это условие противоречит условию (1.59). Если вместо соотношения (1.59) имеет место противоположное неравенство, т.е.

, (1.60)

то совершенно аналогично можно показать, что точка не может принадлежать отрезку .

Пусть, наконец, . В таком случае из рассмотрения исключаются отрезки и .

Алгоритм отыскания локального минимума унимодальной функции

Постановка задачи. Пусть задана унимодальная функция , . Требуется найти такую точку , в которой достигает локального минимума.

Решение поставленной задачи получается в результате выполнения следующих действий

1. Задаем такие две точки и , что , , .

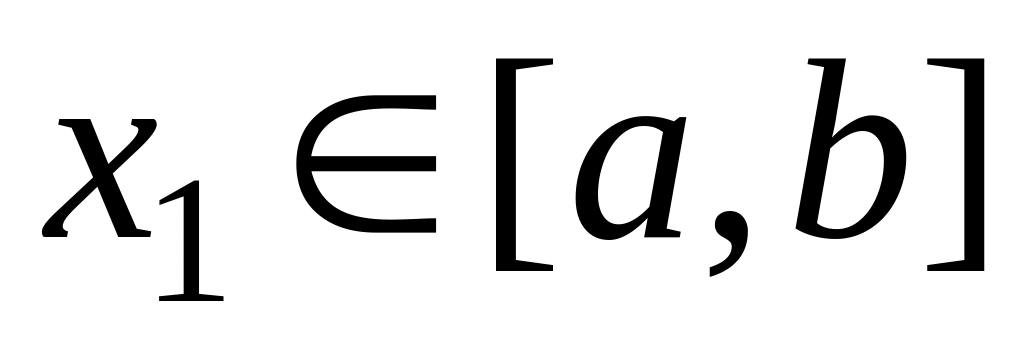2. Вычисляем значения функции и .

3. Если , то из рассмотрения исключается отрезок , если , то отбрасывается отрезок . В том случае, если , то дальнейшему исследованию подлежит отрезок , т.к. вне этого отрезка лежать не может, что можно доказать, опираясь на свойство унимодальности функции f(x).

4. Процесс вычислений заканчивается, как только длина отрезка станет меньше наперед заданного малого числа . В этом случае за принимается координата середины этого малого отрезка.

Остается выяснить, как назначить точки и . В зависимости от этого существуют различные методы, к рассмотрению которых и приступаем.