5.4. Основные результаты раздела

Наблюдаемость линейных систем. Для наблюдаемости системы необходимо u достаточно, чтобы ранг матрицы наблюдаемости

H = (C^T, A^T, C^T,…, (A^T)^n-1, C^T)

был равен n, где n – размерность вектора события .

Наблюдатель полного порядка (фильтр Калмана).

(t) = A z(t) + V[y(t) – C z(t)],

где матрица V выбирается из условия, чтобы матрица (А - VC) имела бы отрицательные собственные значения, или, говорят, была бы устойчивой.

Наблюдатель пониженного порядка (фильтр Люенбергера):

z(t) = G₂(t) + (F + GV) y(t);

₂(t) = (W - VG) [AG₂(t) + Bu(t) + A(GV + F) y(t)]

L = , L^-1= (F,G), (W - VC) AG – устойчивая матрица.

Иначе:

z(t) = Fy(t) + G₁(t),

₁(t) = WA(G₁(t) + Fy(t)) + V[ (t) – CA(Fy(t) + G₁(t))] + (W-VC) Bu(t).

Канонический вид линейных стационарных систем

Если rank H = m < n, то существует матрица Т такая, что = Tx, ^’=TAT^-1 + TBu, y = CT^-1 при этом

где rank = rank H = m < n и матрица определяет обнаруживаемость системы, а именно – система обнаруживаема, если собственные значения имеют неположительные действительные части.

ЗАДАЧИ

1. Определить, какая из систем = Ax + Bu, y = Cx является наблюдаемой, обнаруживаемой, если:

а) б)

в) г)

д) е)

2. Определить, являются ли представленные системы наблюдаемыми. Если нет, то, преобразовав системы к каноническому виду, оценить их обнаруживаемость.

^{a) б)}

^{в) г)}

3. Доказать, что система = Ax + Bu, y = Cx с диагональной матрицей А наблюдаема тогда и только тогда, когда ни один столбец матрицы С не является нулевым. Доказательство:

а) провести непосредственно;

б) получить как следствие наблюдаемости.

4. Доказать, что невырожденное линейное преобразование Т не изменяет наблюдаемость системы = Ax + Bu, y = Cx.

5. Определить, является ли система, описываемая соотношениями

= Ax + Bu, y = Cx,

управляемой и (или) наблюдаемой для следующего частного случая:

Путем выбора конкретных численных значений параметров системы, которые являются:

а) управляемые по состоянию и выходу, ненаблюдаемыми;

б) управляемые по состоянию и наблюдаемые, но неуправляемые по выходу;

в) наблюдаемые с управляемым выходом, но не управляемые по состоянию;

г) управляемые по состоянию, ненаблюдаемые и неуправляемы по выходу;

д) наблюдаемы с управляемым выходом, но с неуправляемым состоянием.

Построить (если есть возможность) наблюдатели полного и пониженного порядка для систем:

^{а) б) в) г)}

Построить наблюдатели пониженного порядка для систем:

^{а) б) в)}

6. Оптимальное управление детерминированными системами

В настоящее время большое внимание уделяется вопросам оптимизации характеристик систем в процессе их функционирования. В частности задача может заключаться в максимизации дальности полета ракеты, максимизации доходов какого-либо предприятия, минимизации экологических потерь при реализации того или иного технологического процесса, минимизации энергии или затрат, требуемых для достижения некоторого заданного состояния системы, минимизации ошибки оценивания состояния объекта. Таких задач, относящихся к системам различного типа и характера, можно указать множество. Исследование управления, с помощью которого может быть достигнута поставленная перед системой цель при условии минимизации (или максимизации) некоторого, определяемого исследователем критерия, является фундаментальной задачей теории оптимального управления.

В реальных условиях эта задача может быть разбита на 4 взаимосвязанных части:

1. Определение цели.

2. Определение положения системы относительно цели (определение состояния системы в фазовом пространстве).

3. Определение внешних факторов, оказывающих влияние на процесс функционирования системы (или эволюцию системы в пространстве состояний).

4. Выбор наилучшей тактики поведения, исходящей из определения цели (1), знания состояния системы (2) и внешних входных воздействий (3).

Прежде всего, для решения задачи оптимизации необходимо определиться с целью функционирования системы. Такой целью может быть достижение заданной точки фазового пространства или некоторой его области. Дополнительно к цели исследователь должен сформулировать условия оценки эффективности движения системы в пространстве и качества достижения цели. Этот этап заканчивается определением критериальной или стоимостной функции (функционала) оптимизационного процесса, которая служит формальной целью эволюции системы. При реализации этого этапа требуется дать соответствующую формулировку и описание задачи в такой форме, чтобы на её основе можно было дать математическое описание системы. Для осуществления эффективного управления системой необходимо знать её текущее состояние. Это – так называемая задача оценки состояния. Кроме того, необходимо описать эволюцию системы с учетом внешних факторов и получить адекватную модель. Это – так называемая задача идентификации системы. После реализации перечисленных задач возможно решение задачи выбора наилучшего или оптимального в смысле заданного критерия.

Сформулируем пять взаимосвязанных задач оптимального управления системами:

1. Задача управления. Рассматривается система заданной структуры и связью между входным управляющим воздействием и состояниями системы x(t). Требуется найти управление, обеспечивающее достижение цели. Если случайные воздействия на систему не учитываются, то получим детерминированную систему оптимального управления. Это может быть задача с разомкнутым контуром (программное управление u(t) (рис 1.1,а)) или замкнутым контуром (управление с обратной связью), в которой управление является функцией состояния u(t,х(t)) (рис 6.1,б)

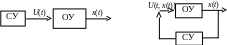
а б

Рис. 6.1. Задача детерминированного управления

ОУ – объект управления, СУ – система управления.

а – программное управление с разомкнутым контуром,

б – управление с обратной связью

3. Задача оценки состояния. Рассматривается известная система со случайным входным воздействием и шумом измерения, так что выходной сигнал y(t) является случайным процессом, отображающим случайную величину вектора состояния x(t). Характеристики шума объекта V₀(t) и шума измерения V_H(t) известны. Требуется найти "наилучшую" оценку истинного состояния системы x(t) по известному y(t).

Рис. 6.2. Задача оценки состояния

ОУ- объект управления, СН – система наблюдения,

СВ – система восстановления

4. Задача стохастического управления. Задача стохастического управления, как показано на рисунке 6.3, состоит из объединения задач 1 и 2. Требуется определить управление u(t), обеспечивающее желаемую эволюцию систем, на основе известного случайного выхода y(t) и сформированной оценки состояния в условиях шумов объекта V₀(t) и наблюдателя V_H(t).

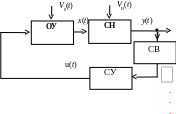
Рис. 6.3. Задача стохастического управления

5. Задача оценивания параметров. Во многих задачах управления необходимо учитывать изменения параметров под воздействиями внешних воздействий. Для этого при известных управлении u(t), выходе y(t) и характеристиках V₀(t), V_H(t) и, если это возможно, имеющейся априорной информации о структуре системы необходимо решить задачу о количественных значениях параметров системы. Предварительно обычно решается задача оценки состояния.

6. Задача адаптивного управления. Задача адаптивного управления является продолжением решения цепочки задач 1-4, реализуемая с помощью целенаправленного изменения (адаптации) параметров системы, обеспечивающего достижение цели. Здесь можно также отметить еще одно направление адаптивного управления, отличное от предыдущего, так называемого "параметрического". Это структурно – адаптивное управление, суть которого состоит в целенаправленной перестройке структуры системы, обеспечивающей достижение цели управления.

В данном разделе будут освещены вопросы, касающиеся решения первой из задач, а именно задачи оптимального управления детерминированными системами для различных условий и ограничений на динамику систем и управления.