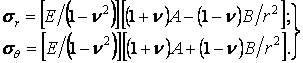- •1.1 Гіпотези й принципи теорії пружності
- •1.2 Напружений стан в точці тіла. Тензор напруг
- •1.2.1 Зовнішні сили й напруги
- •1.2.2 Диференціальні рівняння рівноваги
- •1.2.3 Визначення напруг на похилих площадках. Умови на поверхні
- •1.2.4 Головні напруги. Інваріанти напруженого стану
- •1.2.5 Тензор напруг. Найбільші дотичні напруження
- •1.3 Деформований стан у точці тіла. Тензор деформацій
- •1.3.1 Переміщення й деформації. Взаємозв'язок між ними
- •1.3.2 Об'ємна деформація
- •1.3.3 Рівняння нерозривності деформацій
- •1.3.4 Тензор деформацій. Головні деформації
- •1.4 Взаємозв'язок між тензорами напруг і деформацій. Узагальнений закон Гука
- •1.5 Робота пружних сил. Потенційна енергія деформацій
- •2.1 Повна система рівнянь теорії пружності
- •2.2 Розв’язання задач теорії пружності в переміщеннях
- •2.3 Рішення задачі теорії пружності в напруженнях при постійних об'ємних силах
- •2.4 Типи граничних умов на поверхні тіла
- •2.5 Теорема одиничності. Методи рішення задачі теорії пружності
- •3.1 Плоска деформація і плоский напружений стан
- •3.2 Методи рішення плоскої задачі для прямокутних однозв'язних областей
- •3.3 Згинання консолі силою, прикладеною на кінці
- •3.4 Балка на двох опорах під дією рівномірно розподіленого навантаження
- •3.5 Трикутна підпірна стінка
- •3.6 Розрахунок балки-стінки
- •3.7 Обґрунтування принципу Сен-Венана
- •Розділ 4. ПлосКа задача теорії пружності у полярних координатах
- •4.1 Основні рівняння
- •4.2 Простий радіальний напружений стан
- •4.3 Клин, навантажений у вершині зосередженою силою
- •4.4 Стискання клина
- •4.5 Згинання клина
- •4.6 Дія зосередженої сили, прикладеної до границі напівплощини
- •4.7 Функція напружень для плоскої задачі в полярних координатах
- •4.8 Осесимметричні задачі. Рішення в переміщеннях
- •4.9 Розрахунок труби з товстими стінками (задача Ламе)
- •4.10 Рішення осесимметричної задачі за допомогою функції напружень
- •4.11 Чистий вигин криволінійного бруса. Задача Головіна
- •4.12 Поняття про розрахунок циліндричних котків
- •6.13 Поняття про дію зосередженої сили на пружний півпростір
- •5.1 Основні поняття й гіпотези
- •5.2 Переміщення і деформації в пластинці
- •5.3 Напруження в пластинці
- •5.4 Зусилля в пластинці
- •5.5 Вираження напружень через зусилля
- •5.6 Диференційне рівняння зігнутої серединної поверхні пластинки
- •5.7 Умови на контурі пластинки
- •5.8 Прямокутна пластинка. Рішення Нав’є
- •5.9 Прямокутна пластинка. Розв’язок Леві
- •5.10 Поняття про розрахунок прямокутної пластинки й нескінченної смуги на пружній основі
- •5.11 Основні рівняння вигину круглої пластинки
- •5.12 Найпростіші осесиметричні задачі вигину круглої пластинки
- •5.13 Поняття про розрахунок гнучких пластинок
- •6.1 Сутність варіаційних методів розв’язання
- •6.2 Метод Рітца-Тимошенко
- •6.1 Сутність варіаційних методів розв’язання
- •6.2 Метод Рітца-Тимошенко
- •6.3 Метод Бубнова-Гальоркіна
- •6.4 Метод Власова
- •6.5 Потенційна енергія при вигині пластинки
- •6.6 Приклад розв’язання задачі методом Рітца-Тимошенко
- •6.7 Приклад розв’язання задачі методом Бубнова-Гальоркіна
4.7 Функція напружень для плоскої задачі в полярних координатах
Рішення
плоскої задачі в полярних координатах
у напруженнях полягає у відшуканні
трьох функцій
![]() і
і
![]() ,
за
допомогою
трьох рівнянь: двох рівнянь рівноваги
(4.1) і рівняння нерозривності деформацій
(4.3) при обов'язковому задоволенні умов
на поверхні.
,
за
допомогою
трьох рівнянь: двох рівнянь рівноваги
(4.1) і рівняння нерозривності деформацій
(4.3) при обов'язковому задоволенні умов
на поверхні.
Аналогічно
тому, як було зроблено при рішенні
плоскої задачі в декартових координатах,
рішення в полярних координатах можна
звести до відшукання однієї функції
напружень
![]() .
Виберемо цю функцію так, щоб напруження
виражалися через неї в такий спосіб:
.
Виберемо цю функцію так, щоб напруження
виражалися через неї в такий спосіб:
|
(4.24) |
Підставляючи ці вирази в рівняння рівноваги (4.1), переконуємося, що при відсутності об'ємних сил останні обертаються в тотожності. Щоб перетворити рівняння нерозривності деформацій (4.3), складемо почленно формули для нормальних напружень (4.24)
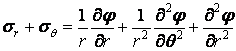 .
.
Права частина цієї суми представлена оператором Лапласа над функцією . Отже,
![]()
і з рівняння (4.3) одержуємо
![]() ,
,
або
|
(4.25) |
У розгорнутому виді рівняння нерозривності деформацій (4.25) записується в такий спосіб:
|
(4.26) |
Таким чином, функція напружень для плоскої задачі в полярних координатах також повинна бути бігармонічною.
4.8 Осесимметричні задачі. Рішення в переміщеннях
Зупинимося на плоских задачах, у яких напруження, а, отже, і функція не залежать від полярного кута . У цьому випадку бігармонічне рівняння (4.26) приймає більш простий вид:
 ,
,
або після диференціювання
|
(4.27) |
Також спрощуються вираз напружень (4.24):
|
(4.28) |
При відсутності об'ємних сил залишиться тільки одне з рівнянь рівноваги (4.1)
|
(4.29) |
Спростяться й геометричні співвідношення Коші (4.4), тому що складова переміщення v в силу симетрії дорівнює нулю:
|
(4.30) |
З формул закону Гука (4.5) залишаться лише дві:
|
(а) |
Осесимметричну задачу в переміщеннях можна вирішити в загальному виді. З формул закону Гука (а) знаходимо
|
(б) |
За допомогою співвідношень (4.30) виключаємо із цих рівнянь складові деформації:
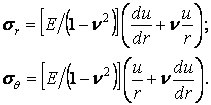
Підставляючи ці напруження в рівняння рівноваги (4.29), одержуємо диференціальне рівняння відносно складового переміщення :
|
(4.31) |
Воно має змінні коефіцієнти. Для рішення приведемо його до рівняння з постійними коефіцієнтами за допомогою наступної підстановки:
|
(4.32) |
або
|
(в) |
Диференціюючи вираз (4.32) по змінній , одержуємо
|
(г) |
Встановимо зв'язок між похідними функції по старій і новій змінним:
![]()
З урахуванням рівності (г) одержуємо
|
(д) |
Друга похідна
|
(е) |
Підставляючи похідні (д) і (е) в рівняння (4.31), знаходимо
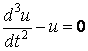 .
.
Рішення цього рівняння має вигляд
![]() .
.
Вертаючись до старої змінної , відповідно до залежностей (4.32) і (в) одержуємо
|
(4.33) |
Знаючи складову переміщення , знаходимо з рівнянь (4.30) складової деформації:
|
(4.34) |
а з формул (б) - складових напружень:
|
(4.35) |
Постійні
й
![]() визначаються із граничних умов.
визначаються із граничних умов.

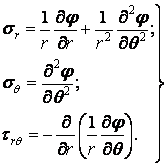
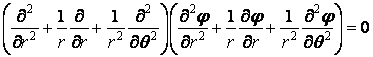 .
.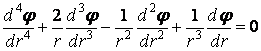 .
.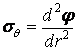 ;
;
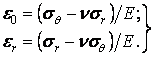
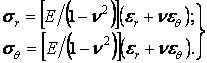
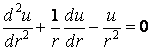 .
.