ЛЕКЦИЯ № 6

3. ЭЛЕМЕНТЫ АЛГЕБРЫ МАТРИЦ

3.1. Основные определения

Система т п чисел (действительных или комплексных), располо­женных в прямоугольной таблице из т строк и п столбцов,

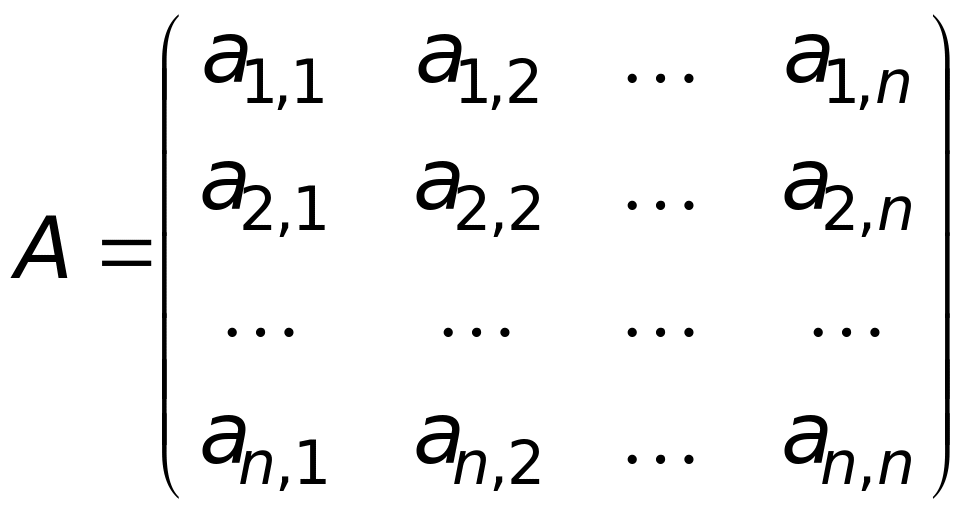(3.1)

называется матрицей. Строки и столбцы таблицы (3.1) называются рядами матрицы.

Числа a_ij (i = 1, 2, .... т; j = 1, 2, . .., n), составляющие дан­ную матрицу, называются ее элементами. Здесь первый индекс i обозначает номер строки элемента, а второй j — номер его столбца.

Для матрицы (3.1) часто употребляется сокращенная запись

А = [ a_ij ] a_ij (i = 1, 2, .... т; j = 1, 2, . .., n) или А = [ a_ij ]_m,n ,

причем говорят, что матрица А имеет тип m n.

Если т = п, то матрица называется квадратной порядка п. Если же т ≠ п, то матрица называется прямоугольной. В частности, матрица типа 1 n называется вектором-строкой, а матрица типа m 1 - вектором-столбцом. Число (скаляр) можно рассматривать как матрицу типа 1 1. Квадратная матрица вида

A = 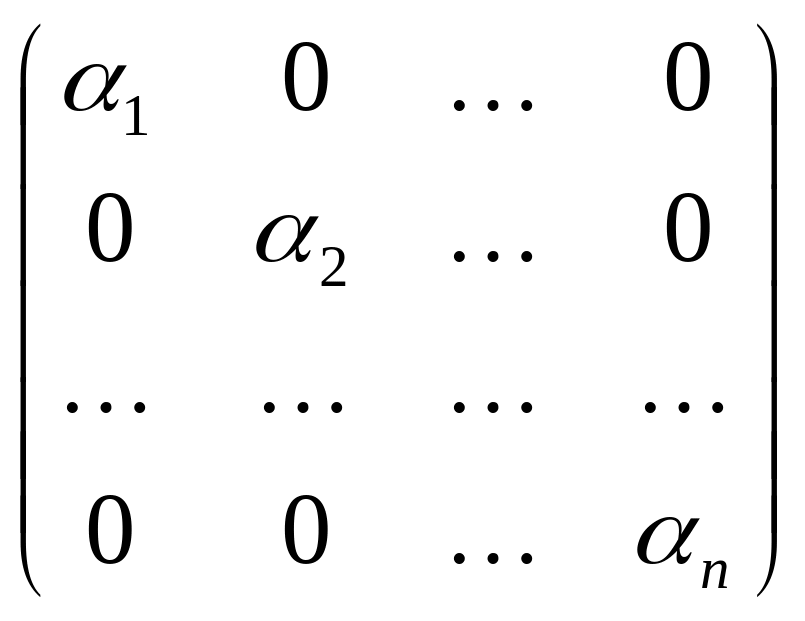(3.2)

называется диагональной и обозначается кратко так: [ ]. Если в (3.2) все α_i = 1, то такая матрица называется единичной и обозначается буквой Е .

3.2. Действия с матрицами

3.2.1. Сумма и разность матриц

Суммой (разностью) двух матриц А = [а_ij ] и B =[b_ij ] одинакового типа называется матрица С = [с_{i j}] того же типа, элементы которой с_{i j} = а_ij + b_ij или

с_{i j} = а_ij - b_ij соответственно.

Из определения суммы матриц непосредственно вытекают сле­дующие ее свойства:

1) А + (В + С) = (А + В) + С;

2) А + В = В + А ;

3) А + 0 = А .

3.2.2. Умножение матриц

а)Умножение матрицы на число

Произведением матрицы А = [а_ij ] на число α (или произведе­нием числа α на матрицу А) называется матрица, элементы которой получены умножением всех элементов матрицы А на число α .

Заметим, что если матрица А - квадратная порядка n, то det α A = α ⁿ det A.

б) Умножение матриц

Пусть А = [а_ij ] и B =[b_ij ] матрицы типов соответственно m n и р q. Если число столбцов матрицы А равно числу строк матрицы В, т. е. п = р, то для этих матриц определена матрица С типа m q называемая их произведением, при этом c_ij = а_i1 b_1j + а_i2 b_2j + … + a_in b_nj , (I = 1, 2,…,m; j = 1, 2,. . ., q).

Из определения вытекает следующее правило умножения матриц: чтобы получить элемент, стоящий в i-й строке и j-м столбце произведения двух матриц, нужно элементы i-й строки первой матрицы умножить на соответствующие элементы j-го столбца второй и полученные произведения сложить.

Произведение АВ имеет смысл тогда и только тогда, когда матрица А содержит в строках столько элементов, сколько элементов имеется в столбцах матрицы В. В частности, можно перемножать квадратные матрицы лишь одинакового порядка.

Произведение двух матриц не обладает переместительным свой­ством, т. е., вообще говоря, АВ ≠ В А, в чем можно убедиться на примерах.

Более того, может даже случиться, что произведение двух матриц, взятых в одном порядке, будет иметь смысл, а произведение тех же матриц, взятых в противоположном порядке, смысла иметь не будет.

В тех частных случаях, когда АВ = В А, матрицы А и В назы­ваются перестановочными (коммутативными). Так, например, как нетрудно убедиться, единичная матрица Е перестановочна с любой квадратной матрицей А того же порядка, причем

АЕ = ЕА = А.Таким образом, единичная матрица Е играет роль единицы при умножении. Если А и В — квадратные матрицы одного и того же порядка, то

det (АВ) = det (ВА) = det A • det В.

Эта формула вытекает из правила перемножения определителей.

в) Обратная матрица

Определение 1. Обратной матрицей по отношению к дан­ной называется матрица, которая, будучи умноженной как справа, так и слева на данную матрицу, дает единичную матрицу.

Для матрицы А обозначим обратную ей матрицу через А^-1. Тогда по определению имеем:

АА^-1 = А^-1 А = Е,

где Е— единичная матрица.

Нахождение обратной матрицы для данной называется обращением данной матрицы.

Определение 2. Квадратная матрица называется неособенной, если определитель ее отличен от нуля.

В противном случае матрица называется особенной, или сингу­лярной.

Теорема. Всякая неособенная матрица имеет обратную матрицу.