12. Минимизация булевых функций на картах Карно

Одним из способов графического представления булевых функций от небольшого числа переменных являются карты Карно, которые строят как развертки кубов на плоскости. При этом вершины куба представляются клетками карты, координаты которых совпадают с координатами соответствующих вершин куба. Карта заполняется так же, как таблица истинности: значение 1 указывается в клетке, соответствующей набору, на котором функция имеет единичное значение. Значения 0 на карте обычно не отмечаются. Пример использования карт Карно для представления функций:

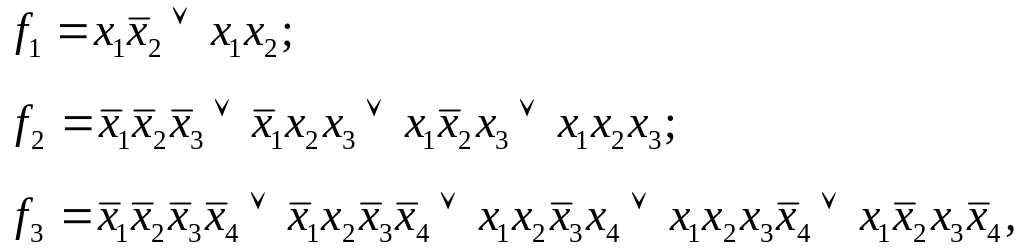
которым соответствуют комплексы:

приведен на рис.1. Клетки отмеченные на картах значениями 1, соответствуют 0-кубам (конституентам единицы) булевых функций.

x1x2
00	01	11	10
		1	1

	х2х3
х1		00	01	11	10
	0	1		1
	1			1	1

а) f₁ б) f₂

	x3x4
x1x2		00	01	11	10
	00	1
	01	1
	11		1		1
	10				1

в) f₃

Рис.1. Карты Карно функций двух (а), трех (б) и четырех (в) переменных.

Карты Карно являются удобным средством для выполнения действий с булевыми функциями и, в частности, используются для минимизации булевых функций от небольшого числа переменных.

С использованием карт Карно легко выделяется минимальное покрытие функции, по которому строится ее минимальная ДНФ или КНФ. Две соседние клетки образуют 1-куб. При этом имеется в виду, что клетки, лежащие на границах карты, также являются соседними по отношению друг к другу. Примеры образования 1-кубов приведены на рис. 2 а,б.

а)

б)

Рис. 2. Образование 1- кубов.

К арты позволяют для функций f₁ и f₂ заданных комплексами

0 00 0000

001 0010

K⁰(f₁) = 011 ; K⁰(f₂) = 1101

100 1111

110 1110

1000

с ценами S^а (f₁) = 15 и S^a (f₂) = 24, определить покрытия

X00 X000

С(f₁) = 0X1 ; C (f₂) = 00X0

1X0 11X1

111X

с ценами S^a(f₁) = 6, S^a(f₂) = 12, которым соответствуют аналитические выражения, являющиеся минимальными ДНФ функций:

Четыре вершины могут объединяться, образуя 2-куб, содержащий две независимые координаты. Примеры образования 2-кубов приведены на рис. 3.

а)	б)	в)

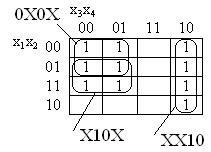
Рис. 3. Образование 2-кубов.

Карты построены для функций f₁, f₂ и f₃, заданных комплексами K⁰(f₁), K⁰(f₂), K⁰(f₃) с ценами S^a(f₁) = 40, S^a(f₂) = 24, S^a(f₃) = 32.

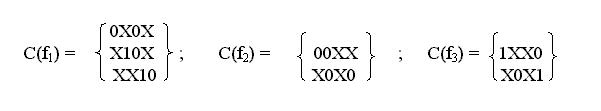
На картах определены покрытия состоящие из 2-кубов и имеющие цены

S^a (f₁) = 6, S^a (f₂) = 4, S^a (f₃) = 4.

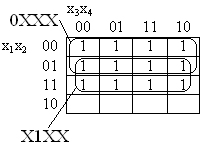
Объединение восьми вершин приводит к образованию 3-куба. Примеры минимизации функций f₁, f₂, f₃, заданных комплексами

0000 0001 0000

0001 0011 0001

0011 0101 0011

0010 0111 0010

0100 1101 1000

K⁰(f₁) = 0101 ; K⁰(f₂) = 1111 ; K⁰(f₃) = 1001 ,

0111 1001 1011

0110 1011 1010

1100 0100 0111

1101 1100 0110

1111 0110 1111

1110 1110 1110

цена каждого из которых равна S^a = 48, приведены соответственно на картах рис. 4, а, б, в. Функциям f₁, f₂, f₃ соответствуют минимальные покрытия с ценой S^а = 2

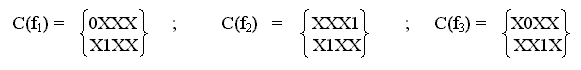
а)	б)	в)

Рис. 4. Образование 3-кубов.

С точки зрения аналитических представлений образование (r+1)-кубов из r - кубов происходит в соответствии с правилом поглощения .

Итак, для получения минимальной ДНФ функции с использованием карты Карно определяется покрытие функции, имеющее минимальную цену. Минимальное покрытие выбирается интуитивным путем на основе анализа различных вариантов покрытий минимизируемой функции. Покрытие с минимальной ценой формируется, если каждая существенная вершина будет покрыта кубом с наибольшим числом независимых компонент и для покрытия всех существенных вершин будет использовано наименьшее число кубов.

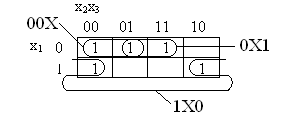
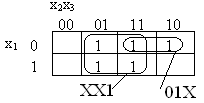
Примеры минимизации функций приведены на рис.5. На рис. 5, а определяется минимальная форма для функции от трех переменных:

XX1

01X

имеющей цену S^а = 15. Минимальному покрытию С(f₁) =

с ценой S^а = 3 соответствует минимальная ДНФ

а)	б)
Рис. 5.Минимизация булевых функций.

На рис. 5,б приведен пример минимизации функции от четырех переменных:

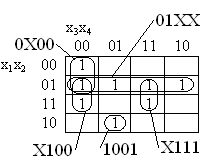
1001

0X00

X100

X111

01XX

с ценой S^а = 32. Минимальному покрытию функции С(f₂) =

с ценой S^а = 15 соответствует минимальная ДНФ:

Минимизация частично определенных булевых функций

При минимизации частично определенных булевых функций в клетки карты Карно, соответствующие наборам аргументов, на которых функция не определена, ставится символ d (don’t care). Эти наборы используются для построения кубов возможно большей размерности, в результате чего уменьшается цена покрытия функции.

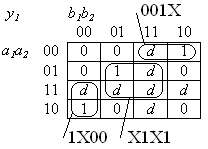
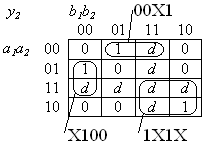
Определим минимальную ДНФ функций, используемых для построения комбинационной схемы, в которой выполняется операция суммирования двоичных кодов по mod 3: у₁у₂ = (а₁а₂ + b₁b₂)_{mod 3}.

Предполагается, что слагаемые имеют значения а₁а₂  2; b₁b₂  2, т.е. наборы а₁а₂ = 11 и b₁b₂ = 11 отсутствуют и рассматриваются как несущественные. Таблицы истинности для функций

y₁ = f₁(a₁,a₂,b₁,b₂); y₂ = f₂(a₁,a₂,b₁,b₂)

представлены на рис. 6 в виде карт Карно. На картах нулевые значения y₁ и y₂ обозначены 0, единичные – 1, несущественные – знаком d.

а)	б)

Рис. 6. Минимизация частично определенных булевых функций.

С использованием несущественных вершин определяются минимальные покрытия:

001X 00X1

C(y₁) = 1X00 ; C(y₂) = X100

X1X1 1X1X

с ценами S^а = 8 каждое, которым соответствуют минимальные ДНФ:

Замечание. После минимизации функция становится полностью определенной. Значения функции на несущественных наборах доопределяется до 1, если набор использовался при минимзации, и до 0, если нет.

В качестве примера использования карт Карно для определения минимальных ДНФ и КНФ функций рассмотрим функцию, представленную на картах рис. 7,а, б.

а)	б)

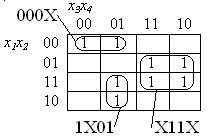
Рис. 7. Определение минимальных ДНФ (а) и КНФ (б) функции.

Данной функции соответствует минимальная ДНФ (рис. 7, а) вида:

Нахождение нулевого покрытия этой функции представлено на рис. 7, б. Минимальная КНФ:

Для минимизации функций от пяти и шести переменных используются соответственно две и четыре четырехмерные карты Карно.

П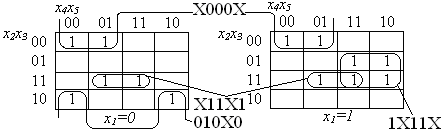 ример использования карт Карно для минимизации функции пяти переменных f =  (0,1,8,10,13,15,16,17,22,23,29,30,31) приведен на рис. 8.

Рис. 8. Минимизация булевой функции от пяти переменных.

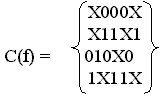
Функции f с ценой S^а = 65

соответствует минимальное покрытие

с ценой S^а = 13.

Принцип размещения карт для представления функций шести переменных показан на рис. 9. На этом рисунке представлена функция от шести переменных, заданная комплексом

с ценой S^а = 48.

Ее минимальное покрытие имеет цену S^а = 8.

При минимизации функций от большого числа переменных карты Карно неудобны, в этом случае для решения задач минимизации используются алгебраические методы. Минимальным ДНФ и КНФ функций соответствуют минимальные двухуровневые логические схемы.

Экономия оборудования, составляющего логическую схему, может быть получена на основе скобочных форм булевых функций, используемых для синтеза логических схем.

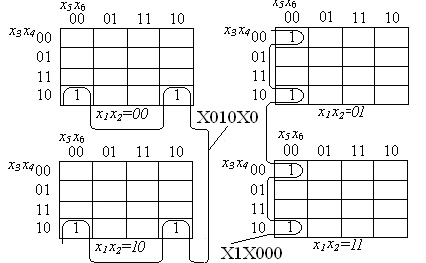
Рис. 9. Карты Карно функции шести переменных.

Так, булевой функции

f(x₁,x₂,x₃,x₄,x₅) =  (5,6,7,13,14,15,21,22,23,25,26,27,29,30,31)

соответствует минимальная ДНФ: f = x₃x₄  x₃x₅ x₁x₂x₄  x₁x₂x₅,

по которой строится двухуровневая логическая схема (рис. 10, а) с ценой

S^b = 14. Минимальная ДНФ преобразуется в скобочную форму:

f = (x₁x₂  x₃)x₄  (x₁x₂  x₃)x₅ = (x₁x₂  x₃) (x₄  x₅),

по которой строится схема (рис. 10, б) с ценой S^b = 8.

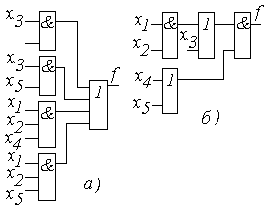
Рис. 10. Схема, построенная по МДНФ (а) и по скобочной форме (б).