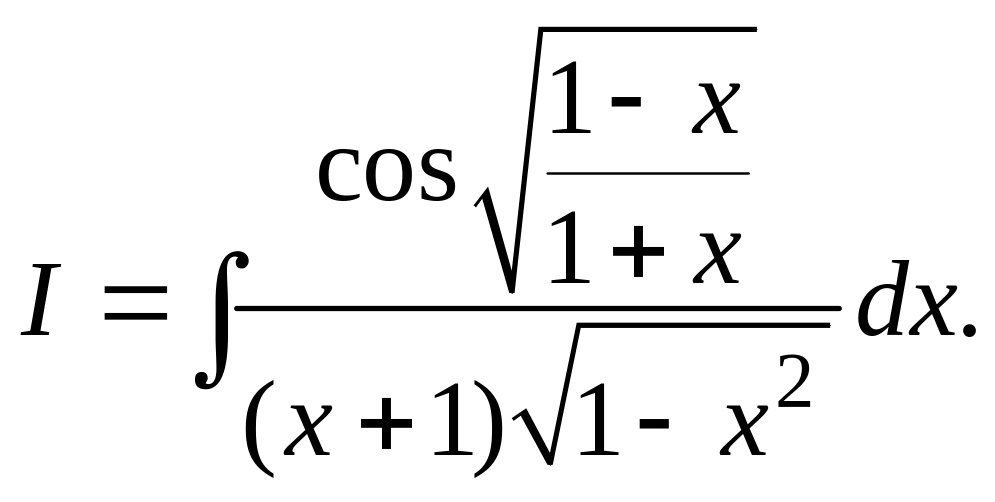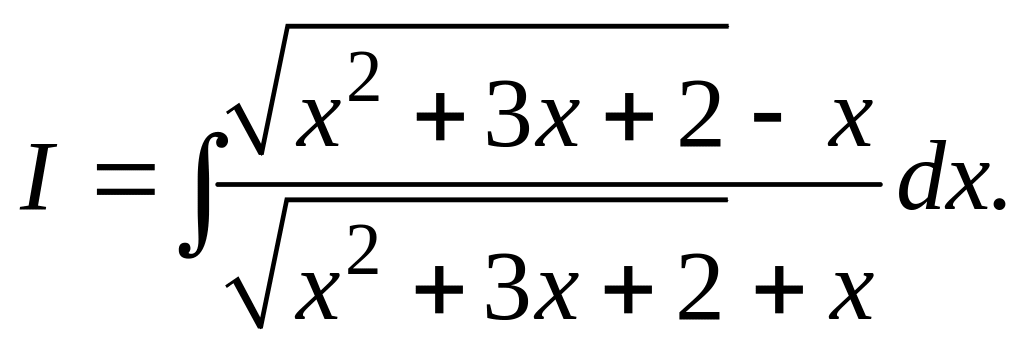Задачи для самостоятельного решения
Вычислить следующие интегралы.
5.5.
5.6.
5.7.
5.8.
§ 6. Интегрирование иррациональных функций
В
этом параграфе мы рассмотрим некоторые
часто встречающиеся интегралы от
иррациональных функций, которые с
помощью подходящих подстановок
рационализируются, т.е. сводятся к
интегралам от рациональных функций.
Через
будем обозначать функцию, рациональную
относительно каждой из переменных
Например,
R(x,
u, v),
Интеграл
рационализируется, т.е. сводится к
интегралу от рациональной функции одной
переменной
подстановкой
,
где N
– наименьшее общее кратное чисел
Аналогично подстановкой
рационализируется интеграл
,
.
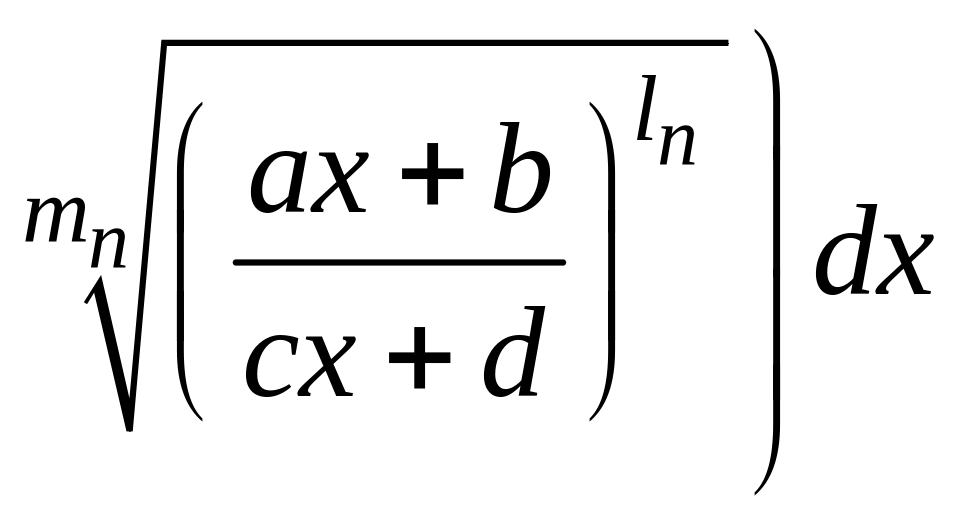Рассмотрим примеры.
Решение. Поскольку НОК(3, 6) = 6, то
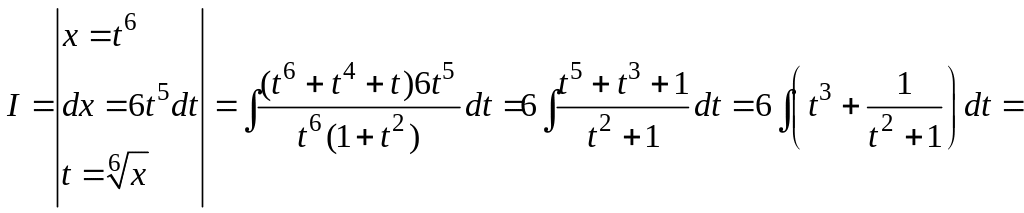
Решение. Сначала мы преобразуем подынтегральную функцию, затем сделаем замену переменной
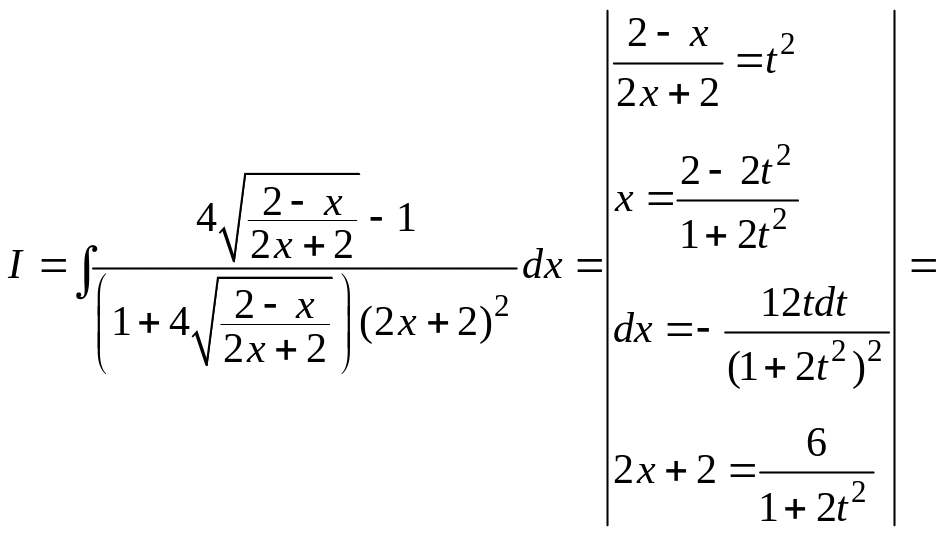
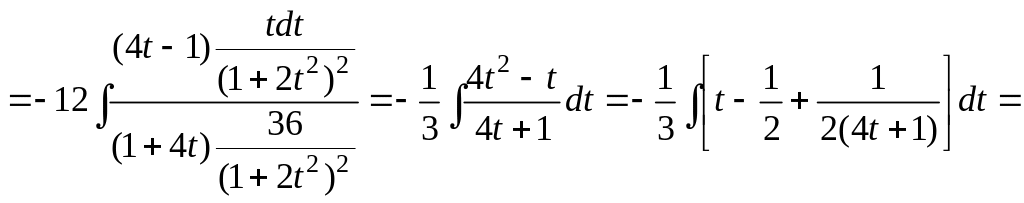
Решение. Преобразуем подынтегральную функцию и сделаем замену переменной
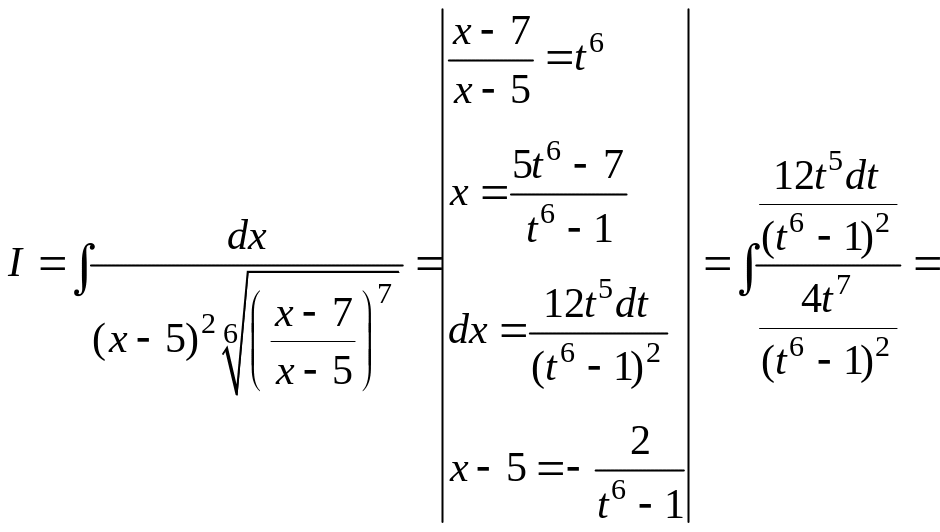
Решение. Преобразуем подынтегральное выражение и сделаем замену переменной
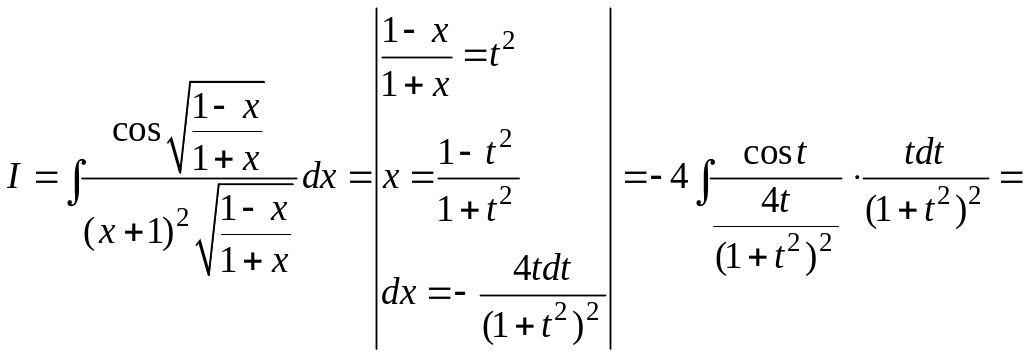
Рассмотрим
интегралы вида
Эти интегралы можно вычислить с помощью
подстановок Эйлера. Мы рассмотрим здесь
две из них.
Если
трехчлен
не имеет действительных корней, то
необходимо a
> 0, в противном случае под корнем будет
отрицательная величина. В этом случае
можно применить следующую подстановку
Эйлера:
(или
).
Тогда
Отсюда находим
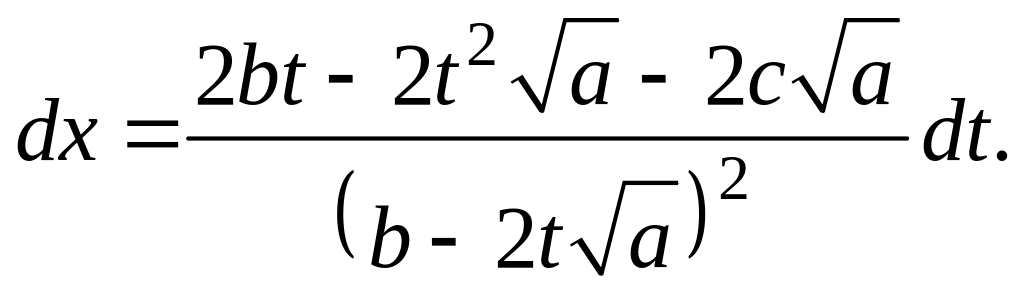
После
подстановки мы получаем интеграл вида
,
где
–
рациональная функция одной переменной.
Если
a
< 0, то трехчлен
обязательно должен иметь действительные
корни. Пусть это будут
Тогда
В этом случае можно применить следующую
подстановку Эйлера:
Рассмотрим примеры.
Решение.
Делаем подстановку
Тогда
После
подстановки в интеграл получаем
.
Для нахождения коэффициентов A, B и C мы имеем уравнение
Подставляя
t
= 0, находим A
= 2. Подставляя t
= ½, находим B
= 3. Чтобы найти C,
сравним коэффициенты при
Получаем 2 = 4A
+ 2C.
Следовательно, C
= –3.
Вычисляем интеграл
Решение.
Поскольку трехчлен имеет корни
то применим подстановку
Тогда
После подстановки получаем
Разложим подынтегральную функцию на простейшие дроби:
Приводим дроби в правой части к общему знаменателю и приравниваем числители получившихся дробей. Получаем равенство
Полагая t = 1, находим E = –3/8. Полагая t = –1, находим B = –1/6. Полагая t = 2, находим A = 8/27. Чтобы найти оставшиеся коэффициенты, положим сначала t = 0, затем t = –2. Получим с учетом, что коэффициенты A, B и E известны, два уравнения для нахождения коэффициентов C и D:
2C + 2D = A – 2B +2E,
12C – 12D = 3A +12B +4E
или
C + D = A/2 –B + E,
C – D = A/4 + B + E/3.
Подставляя
сюда найденные значения для A,
B,
E,
решаем систему относительно C
и D.
Получаем C
=
.
Вычисляем интеграл
где
Подстановки Эйлера часто приводят к громоздким выкладкам, поэтому часто имеет смысл поискать другие способы вычисления. Для вычисления многих интегралов вида
существуют более простые приемы.
Интегралы вида
,
где
–
многочлен степени n,
вычисляются с помощью формулы
.
Здесь
–
многочлен степени не выше n
– 1, а λ – некоторое постоянное число.
Дифференцируя обе части формулы и затем
умножая на
,
получаем равенство многочленов, из
которого находим λ и коэффициенты
многочлена
Интеграл в правой части формулы рассмотрен
в § 4.
К интегралам рассмотренного типа сводятся интегралы вида
Для этого надо сделать подстановку x – α = 1/t.
Рассмотрим примеры.
Решение. Представим наш интеграл в следующем виде:
Продифференцируем
это равенство и после этого домножим
на
.
Получим
.
Приравнивая коэффициенты при одинаковых степенях x, получаем систему уравнений
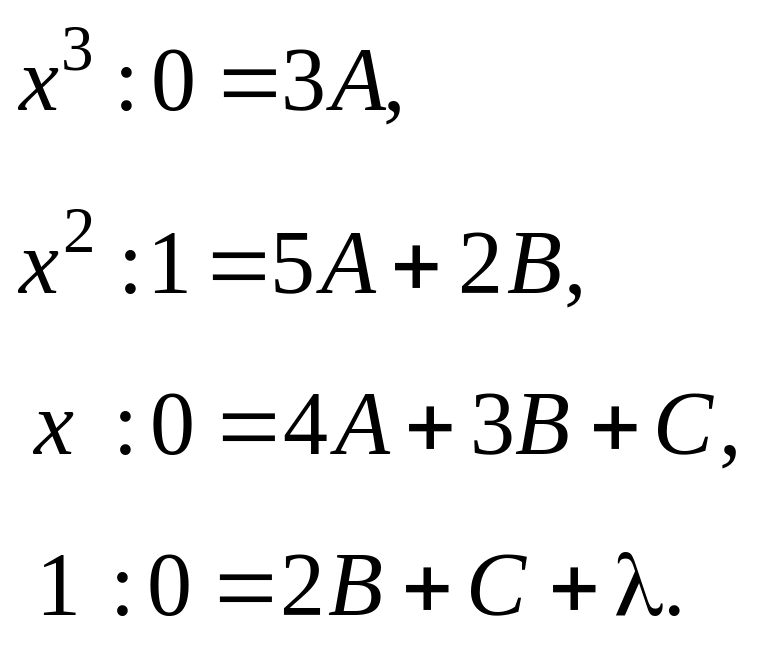
Решая систему, находим A = 0, B = 1/2, C = –3/2, λ = 1/2. Отсюда следует
Решение. Делаем замену переменной
Получаем
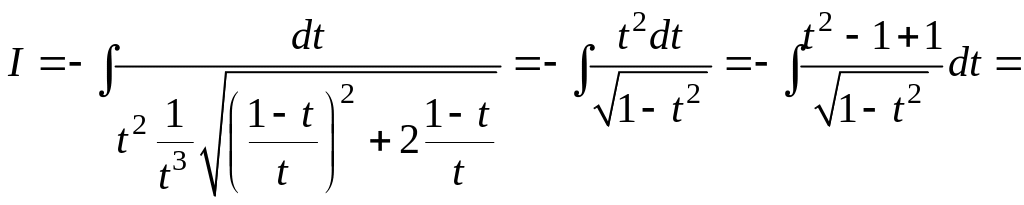
Интегралами от дифференциального бинома называются интегралы вида
,
где m, n, p – рациональные числа. Эти интегралы сводятся к интегралам от рациональных функций в следующих трех случаях:
а)
p
– целое
число. Тогда интеграл рационализируется
подстановкой
где N
– общий знаменатель дробей m
и n;
б)
–
целое число. Тогда применяем подстановку
где N
– знаменатель дроби p;
в)
–
целое число. В этом случае делаем
подстановку
где N
– знаменатель p.
Доказано, что если ни одно из этих трех условий не выполняется, то интеграл от дифференциального бинома не может быть выражен через элементарные функции (теорема Чебышева).
Рассмотрим примеры.
Решение.
Так как здесь m
= –1/3, n
= 1/6, p
= –1, то у нас
– случай a).
Делаем подстановку
Тогда
Решение. Здесь m = –1/2, n = 1/4, p = 1/3. Так как
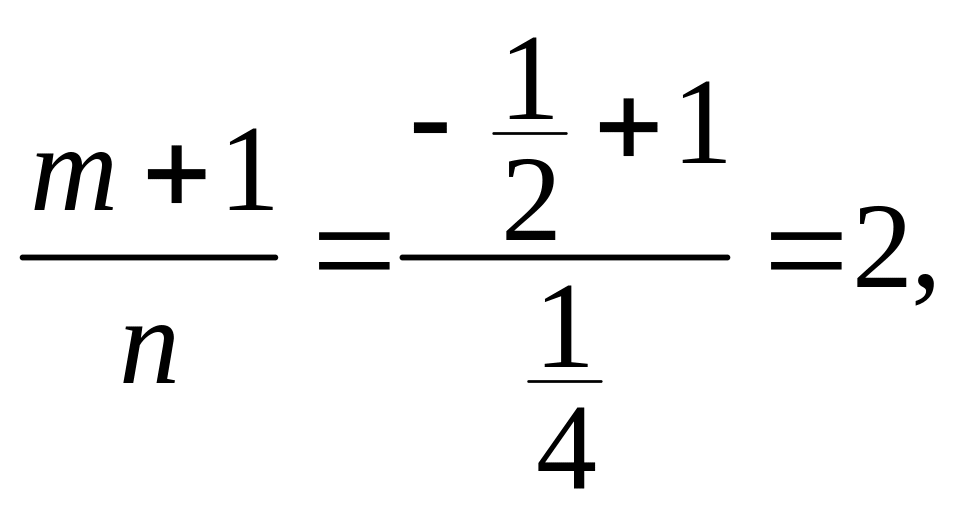
то
делаем подстановку
Тогда
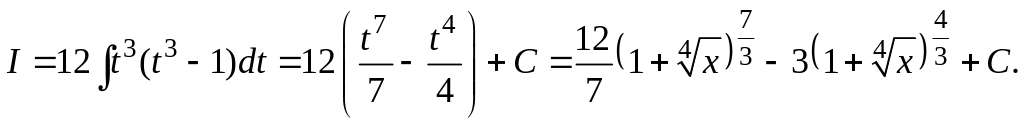
Решение.
В этом примере
–
целое число. Применяем подстановку
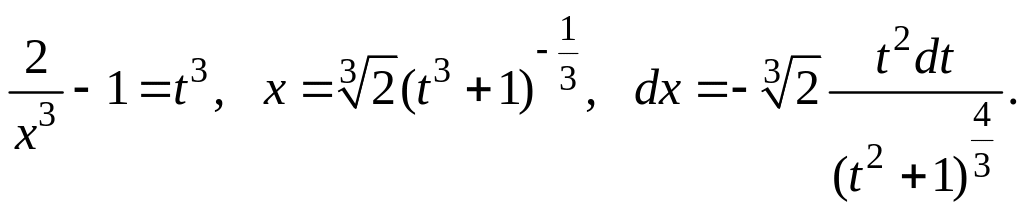
Тогда
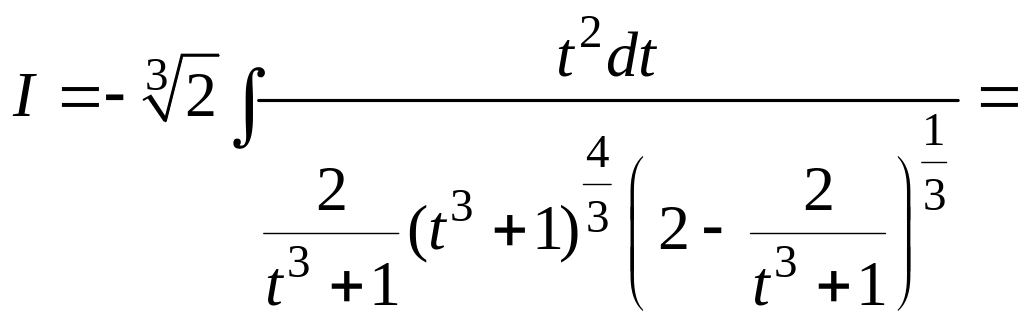
