5.2.3. Основні характеристики функції

1.Функция , визначена на множині , називається парною, якщо виконуються умови ; непарної якщо виконується умови .

Графік парної функції симетричний відносно осі , а непарної – відносно початку координат.

Наприклад, - парні функції; а 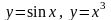– непарні функції ; - функції загального вигляду, тобто не парні і не непарні.

2.Нехай функція визначена на множині і нехай . Якщо для будь-яких значень аргументів з рівності випливає нерівність : , то функція називається зростаючою на множині ; , то функція називається неспадною на множині ; , то функція називається спадною на множині ; ,то функція називається незростаючою на множині .

Рис.100

Наприклад, функція, задана графіком (див. рис. 100), спадає на інтервалі (-2; 1), неспадає на інтервалі(1; 5), зростає на інтервалі(3; 5).

Зростаючі, незростаючі, спадні і неспадні функції на множині називається монотонними на цій множині, а зростаючі і спадні – строго монотонними. Інтервали, в яких функція монотонна, називається інтервалами монотонності. На малюнку (вище) функція строго монотонна на (-2; 1) і (3; 5); монотонна на (1; 3).

3 .Функцию , визначену на множині , називають обмеженою на цій множині, якщо існує таке число 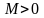, що для всіх виконується нерівність (короткий запис : , , називається обмеженою на , якщо : . Звідси випливає, що графік обмеженої функції лежить між прямими (див. рис.101).

Рис.101

4. Функція , визначена на множині , називається періодичною на цій множині, якщо існує таке число , що при кожному значення . При цьому число називається періодом функції. Якщо - період функції, то її періодами будуть також числа , де . Так, для періодами будуть числа .Основний період (якнайменший додатній) – це період . Взагалі звичайно за основний період беруть якнайменше додатне число , що задовольняє рівності .

5.2.4. Обернена функція

Нехай задана функція з областю визначення і множиною значень . Якщо кожному значенню відповідає єдине значення , то визначена функція з областю визначення і множиною значень . (див. рис.102).

Рис.102

Така функція називається зворотною до функції і записується в наступному вигляді : . Про функції і говорять, що вони є взаємно оберненими. Щоб знайти функцію , обернену до функції , достатньо розв’язати рівняння щодо (якщо це можливо).

Приклади :

1.Для функції оберненою функцією є функція ;

2.Для функції , [0; 1], оберненої не існує, оскільки одному значенню у відповідає два значення х (так, якщо = то =, =).

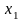З визначення оберненої функції випливає, що функція має обернену тоді і тільки тоді, коли функція задає взаємно однозначну відповідність між множинами і .Звідси випливає, що будь-яка строго монотонна функція має зворотну. При цьому якщо функція зростає (спадає), то обернена функція також зростає(спадає).

Звернимо увагу, що функція і обернена їй зображаються одній і тій же кривій, тобто графіки їх співпадають. Якщо ж умовитися, що, як завжди, незалежну змінну (тобто аргумент) позначити через х, а залежну змінну через , то функція обернена функції запишеться у вигляді

Це означає, що точка кривої стає точкою кривої Але точки симетричні щодо прямої = (див. рис. 103).

Тому графіки взаємно обернених функцій і симетричні щодо бісектриси першого і третього координатних кутів.