Лабораторная работа № 4

СЛУЧАЙНЫЕ ПРОЦЕССЫ И ИХ ХАРАКТЕРИСТИКИ

4.1. ЦЕЛЬ РАБОТЫ

Ознакомление с основными понятиями теории случайных процессов. Выполнение измерений моментных характеристик и оценки ПРВ мгновенных значений случайных процессов. Анализ вида автокорреляционной функции (АКФ) и спектральной плотности мощности (СПМ) случайного процесса. Исследование преобразований случайного процесса линейными стационарными и нелинейными безынерционными цепями.

4.2. ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

Случайные события и случайные величины

Событие , которое может произойти или не произойти в некотором опыте, называется случайным событием и характеризуется вероятностью осуществления . Случайная величина (СВ) может принять в опыте одно значение из некоторого множества ; это значение называется реализацией данной СВ. может быть, например, множеством вещественных чисел или его подмножеством. Если множество конечно или счетно (дискретная СВ), можно говорить о вероятности осуществления события, которое заключается в принятии случайной величиной значения , т. е. на множестве значений дискретной случайной величины задается распределение вероятностей . Если множество несчетно (например, вся вещественная прямая), то полное описание случайной величины дает функция распределения, определяемая выражением

,

где . Если функция распределения непрерывна и дифференцируема, то можно определить плотность распределения вероятностей (ПРВ), называемую также для краткости плотностью вероятности (а иногда просто плотностью):

, при этом .

Очевидно, функция распределения – неотрицательная неубывающая функция со свойствами , . Следовательно, ПРВ – неотрицательная функция, удовлетворяющая условию нормировки .

Иногда ограничиваются числовыми характеристиками случайной величины, чаще всего моментами. Начальный момент -го порядка ( -й начальный момент)

,

где горизонтальная черта и – символические обозначения интегрального оператора усреднения по ансамблю. Первый начальный момент , называется математическим ожиданием или центром распределения.

Центральный момент -го порядка ( -й центральный момент)

.

Наиболее употребительным из центральных моментов является второй центральный момент, или дисперсия

.

Вместо дисперсии часто оперируют среднеквадратическим отклонением (СКО) случайной величины .

Средний квадрат, или второй начальный момент , связан с дисперсией и математическим ожиданием:

.

Для описания формы ПРВ используют коэффициент асимметрии и коэффициент эксцесса (иногда эксцесс характеризуют величиной ).

Часто используется нормальное, или гауссовское (гауссово), распределение с ПРВ

,

где и – параметры распределения (математическое ожидание и СКО соответственно). Для гауссовского распределения , .

Две случайные величины и характеризуются совместной плотностью распределения . Числовыми характеристиками совместной плотности служат начальные и центральные смешанные моменты

, ,

где и – произвольные целые положительные числа; и – математические ожидания СВ x и y.

Наиболее часто используются смешанные моменты второго порядка – начальный (корреляционный момент):

и центральный (ковариационный момент, или ковариация)

.

Для пары гауссовских случайных величин двумерная совместная ПРВ имеет вид

где , – среднеквадратические отклонения; – математические ожидания; – коэффициент корреляции – нормированный ковариационный момент

.

При нулевом коэффициенте корреляции очевидно,

,

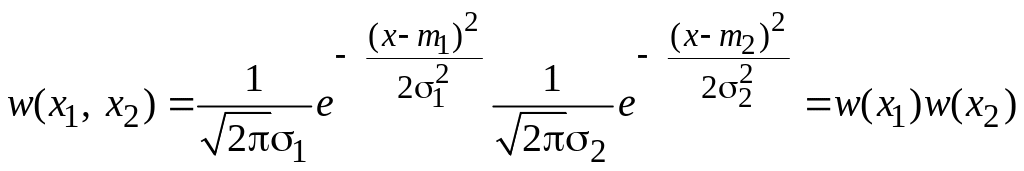т. е. некоррелированные гауссовские случайные величины независимы.