6.3. Formulas for computing the vector of a particular solution of inhomogeneous system of differential equations.

Instead of the formula for computing the vector of a particular solution of an inhomogeneous system of differential equations in the form [Gantmaher]:

it is proposed to use the following formula for each individual section of the integration interval:

.

The correctness of the above formula is confirmed by the following:

,

,

,

,

,

,

which was to be confirmed.

The calculation of the vector of a particular solution of a system of differential equations is performed using the representation of Cauchy’s matrix under the integral sign in the form of a series and integrating this series elementwise:

This formula is valid for the case of a system of differential equations with constant coefficient matrix =const.

Let us consider the variant, when the steps of the integration interval are chosen sufficiently small, which allows us to consider the vector in the region approximately as a constant , which allows us to remove this vector from the signs of the integrals:

It is known that when T=(at+b) we have

In our case, we have

Then we obtain .

Then we obtain a series for computing the vector of a particular solution of an inhomogeneous system of differential equations on a small section :

For the case of differential equations with variable coefficients, an averaged matrix of the coefficients of the system of differential equations can be used for each section.

If the considered section of the integration interval is not small, then the following iterative (recurrent) formulas are proposed.

We give the formulas for computing the vector of a particular solution, for example, on the considered section through the vectors of the particular solution , , , corresponding to the subsections , , .

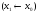We have .

We also have a formula for a separate subsection:

.

We can write:

,

.

We substitute in and get:

.

Let us compare the expression obtained with the formula:

and we get, obviously, that:

and for the particular vector we obtain the formula:

.

That is, the subsector vectors are not simply add with each other, but with the participation of Cauchy’s matrix of the subsection.

Similarly, we write down and substitute the formula for and get:

Comparing the expression obtained with the formula:

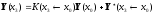
obviously, we get that:

and together with this we get the formula for a particular vector:

_{That is, in this way a particular vector is calculated - the vector of the particular solution of the inhomogeneous system of differential equations, that is, for example, a particular vector on the considered section is calculated through the computed partial vectors} , , _{corresponding to the sub-sections} , , _.

6.4. Applicable formulas for orthonormalization.

Taken from [Berezin, Zhidkov]. Let there be given a system of linear algebraic equations of order n:

=.

Here, above the vectors, we draw dashes instead of their designation in boldface.

We will consider the rows of the matrix of the system as vectors:

=(,,…,).

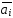We orthonormalize this system of vectors.

The first equation of the system = we divide by .

In doing so, we get:

++…+=, =(,,…,),

where =, =, =1.

The second equation of the system is replaced by:

++…+=, =(,,…,),

where =, =,

=-(,), =-(,).

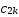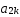Similarly we proceed further. The equation with the number i takes the form:

++…+=, =(,,…,),

where =, =,

=-(,)-(,)-…-(,),

=-(,)-(,)-…-(,).

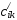Here (,) is the scalar multiplication of vectors.

The process will be realized if the system of linear algebraic equations is linearly independent.

As a result, we come to a new system 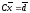, where the matrix will be with orthonormal rows, that is, it has the property , where is the identity matrix.

Chapter 7. The simplest method for solving boundary value problems with stiff ordinary differential equations without orthonormalization - the method of "conjugation of sections of the integration interval", which are expressed by matrix exponents.

The idea of overcoming the difficulties of computation by dividing the interval of integration into conjugate areas belongs to Dr.Sc. Professor Yu.I.Vinogradov (his doctoral thesis was defended including on this idea), and the simplest realization of this idea through the formulas of the theory of matrices belongs to the Ph.D. A.Yu.Vinogradov.

We divide the interval of integration of the boundary value problem, for example, into 3 sections. We will have points (nodes), including edges:

.

We have boundary conditions in the form:

We can write the matrix equations of conjugation of sections:

,

,

.

We can rewrite it in a form more convenient for us further:

,

,

.

where is the identity matrix.

Then in a combined matrix form we obtain a system of linear algebraic equations in the following form:

.

This system is solved by Gauss’ method with the separation of the main element.

At points located between nodes, the solution is to be solved by solving Cauchy’s problems with the initial conditions in the i-th node:

.

It is not necessary to apply orthonormalization for boundary value problems for stiff ordinary differential equations, since on each section of the integration interval the calculation of each matrix exponent is fulfilled independently and from the initial orthonormal identity matrix, which makes it unnecessary to use orthonormalization, unlike S.K.Godunov’s method, which greatly simplifies programming in comparison with S.K.Godunov's method.

It is possible to calculate Cauchy’s matrices not in the form of matrix exponents, but with Runge-Kutta’s methods from the starting identity matrix, and the vector of the particular solution of the inhomogeneous system of differential equations can be calculated on each site by Runge-Kutta’s methods from the starting zero vector. In the case of Runge-Kutta’s methods, error estimates are well known, which means that calculations can be performed with a known accuracy.

Chapter 8. Calculation of shells of composite and with frames by the simplest method of "conjugation of sections of the integration interval".

8.1. The variant of recording of the method for solving stiff boundary value problems without orthonormalization - the method of "conjugation of sections, expressed by matrix exponents "- with positive directions of matrix formulas of integration of differential equations.

We divide the interval of integration of the boundary value problem, for example, into 3 sections. We will have points (nodes), including edges:

.

We have boundary conditions in the form:

We can write the matrix equations of conjugation of sections:

,

,

.

We can rewrite it in a form more convenient for us further:

,

,

.

where is the identity matrix.

As a result, we obtain a system of linear algebraic equations:

.

This system is solved by Gauss’ method with the separation of the main element.

It turns out that it is not necessary to apply orthonormalization, since sections of the integration interval are chosen so long that the computation on them is stable.

At points near the nodes, the solution is found by solving the corresponding Cauchy’s problems with the origin at the i-th node:

.