8.2. Composite shells of rotation.
Let us consider the conjugation of segments of the composite shell of rotation.
Suppose we have 3 sections, where each section can be expressed by its differential equations and the physical parameters can be expressed differently - different formulas on different sections:
In the general case (for the example of section
12), the physical parameters of the section (vector
)
are expressed in terms of the required parameters of the system of
ordinary differential equations of this section (through the vector
)
as follows:
,
where the matrix
is a square non-degenerate matrix.
With the transition of the conjugation point, we
can write in a general form (but using the conjugation point
):
,
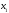where
is the discrete increment of physical
parameters (forces, moments) during the transition from the "01"
section to the "12" section, and the square nondegenerate
matrix
is diagonal and consists of units and
minus ones on the main diagonal to establish the correct
correspondence between the positive
directions of forces, angular momenta,
displacements and angles when going from "01" to "12",
which may be different (in different differential equations of
different conjugate regions) in the equations to the left of the
conjugation point and in the equations to the right of the
conjugation point.
The last two equations combine to form the equation:
.
At
the conjugation point
,
we similarly obtain the equation:
.
If the shell consisted of identical parts, then we could write in a combined matrix form a system of linear algebraic equations in the following form:
.
But in our case the shell consists of 3 sections, where the middle section can be considered, for example, a frame expressed in terms of its differential equations.
Then instead of vectors
,
,
,
we should consider vectors:
.
Then the matrix equations
,
,
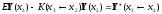
will take the form:
,
,
,
,
.
After rearranging the summands, we get:
,
,
,
,
.
As a result, we can write down the final system of linear algebraic equations:
This system is solved by the Gauss method with the separation of the main element.
At points located between nodes, the solution is to be solved by solving Cauchy’s problems with the initial conditions in the i-th node:
.
It is not necessary to apply orthonormalization for boundary value problems for stiff ordinary differential equations.
8.3. Frame, expressed not by differential, but algebraic equations.
Let us consider the case when the frame (at a
point
)
is expressed not in terms of differential equations, but in terms of
algebraic equations.
Above we wrote down that:
We can represent the vector
of force factors and displacements in
the form:
,
where
is the displacement vector,
is the vector of forces and moments.
Algebraic equation for the frame:
,
where
G is the
matrix of the rigidity of the frame, R
is the vector of the frame movements,
is the vector of force factors that
act on the frame.
At the point of the frame we have:
,
that
is, there is no discontinuity in the movements
,
but there is a resultant vector of force factors
,
which consists of forces and moments on the left plus forces and
moments to the right of the point of the frame.
,
,
,
,
,
где
,
which is true if we do not forget that in this case we have:
,
that
is, the vector of displacements and force factors is first compiled
from displacements (above)
,
and then from force factors (below)
.
Here it is necessary to remember that the
displacement vector
is expressed in terms of the required
state vector
:
,
,
where
for convenience was introduced re-designation
.
Then we can write:
,
We write the matrix equations for this case:
,
,
.
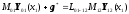Let us write the vector
in the equation:
,
.
To ensure the non-cumbersomeness, we introduce the notation:
.
Then equation
will take the form:
.
For convenience, we rearrange the terms in the matrix equations so that the resulting system of linear algebraic equations is written clearly:
,
,
.
Thus, we obtain the resulting system of linear algebraic equations:
.
If an external force-moment action
is applied to the frame, then
should be rewritten in the form
,
then:
.
Then the matrix equation
will take the form:
,
.
The resulting system of linear algebraic equations takes the form:
.