Полином Ньютона.

i	0	1	2	3	4	5
x	1,2	1,3	1,4	1,5	1,6	1,7
y	4,018	4,025	4,035	4,048	4,012	4,028

Рассчитаем конечные разности:

∆у₀=у₁-у₀ ∆²у₀=∆у₁-∆у₀ ∆³у₀=∆²у₁-∆²у₀ ∆⁴у₀=∆³у₁-∆³у₀ ∆⁵у₀=∆⁴у₁-∆⁴у₀

∆у₁=у₂-у₁ ∆²у₁=∆у₂-∆у₁ ∆³у₁=∆²у₂-∆²у₁ ∆⁴у₁=∆³у₂-∆³у₁

∆у₂=у₃-у₂ ∆²у₂=∆у₃-∆у₂ ∆³у₂=∆²у₃-∆²у₂

∆у₃=у₄-у₃ ∆²у₃=∆у₄-∆у₃

∆у₄=у₅-у₄

Полученные данные сведем в таблицу:

	у	∆у	∆^2у	∆^3у	∆^4у	∆^5у
0	4,018	0,007	0,003	8,88178E-16	-0,052	0,205
1	4,025	0,01	0,003	-0,052	0,153
2	4,035	0,013	-0,049	0,101
3	4,048	-0,036	0,052
4	4,012	0,016
5	4,028

Интерполяционная формула Ньютона:

P₅(x)=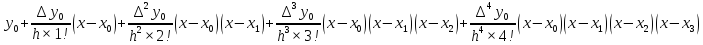

По условию задачи h=0,1.

Построим получившийся график.

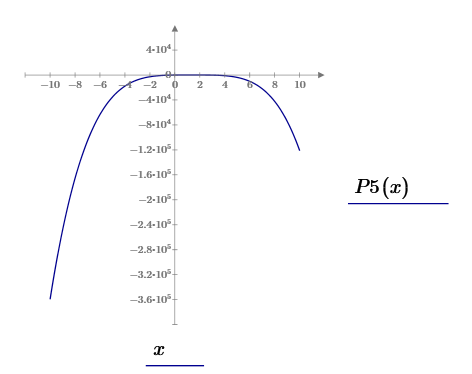
Произведем проверку:

После проведенной проверки найдем F(х^*)

P5(1.25)= 4.023156

Найдем погрешность:

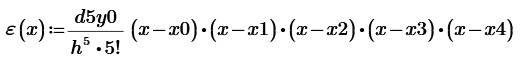
Полином Лагранжа.

R_n(x)=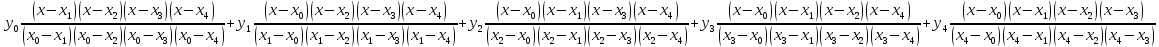

Проверим полином по табличным координатам:

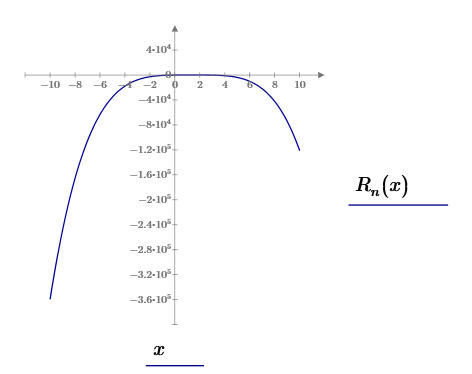
По полученному полиному вычисляем R(х^*) и R(х^**):

R(х^*)→Р(1.25)= 4.023156

R(х^**)→Р(1.75)= 3.624406

Проведем оценку погрешности:

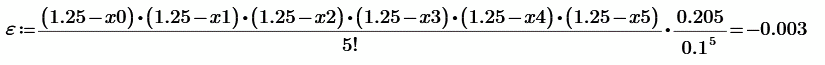
ЗАДАЧА № 3

Найти наименьший положительный корень уравнения комбинированным методом с точностью до 0,0001. Уравнение: lg(2x) –

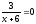
Краткая теоретическая часть:

Методы хорд и касательных дают приближения корня с разных сторон. Поэтому их часто применяют в сочетании друг с другом, и уточнение корня происходит быстрее.

Пусть дано уравнение f(x)=0, корень ξ отделён и находится на отрезке [a,b].

Если f (x)·f ″(x) < 0, то методом хорд получаем значение корня с избытком, а методом касательных – с недостатком.

Если f (x)·f ″(x) > 0, то метод хорд даёт приближение корня с недостатком, а метод касательных – с избытком.

Рассмотрим случай, когда f (b) < 0, f ″(x) > 0 (рис.1), то со стороны конца а лежат приближённые значения корня, полученные по методу касательных, а со стороны конца b – значения, полученные по методу хорд.

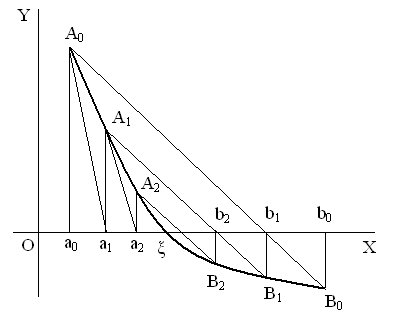
Рис.1 Иллюстрация комбинированного метода.

Тогда , .

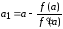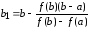Теперь истинный корень ξ находится на интервале [a₁,b₁]. Применяя к этому интервалу комбинированный метод, получаем:

,

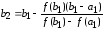
и вообще

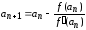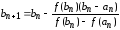, . (1)

Для случая, когда f (b)·f ″(x) > 0, то рассуждая аналогично, получим следующие формулы для уточнения корня уравнения:

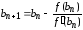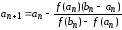, . (2)

Комбинированный метод очень удобен при оценке погрешности вычислений. Процесс вычислений прекращается, как только станет выполняться неравенство

‌‌‌‌‌‌‌ |b_n+1–a_n+1| < ε.

Корень уравнения есть среднее арифметическое последних полученных значений: ξ=(‌a_n+1+b_n+1)/2

Решение:

Сначала найдем точное решение в Mathcad

х=1,2897305718

Построим графики Функции и 2х ее производных, где m(x)=f `(x), p(x)=f ``(x)

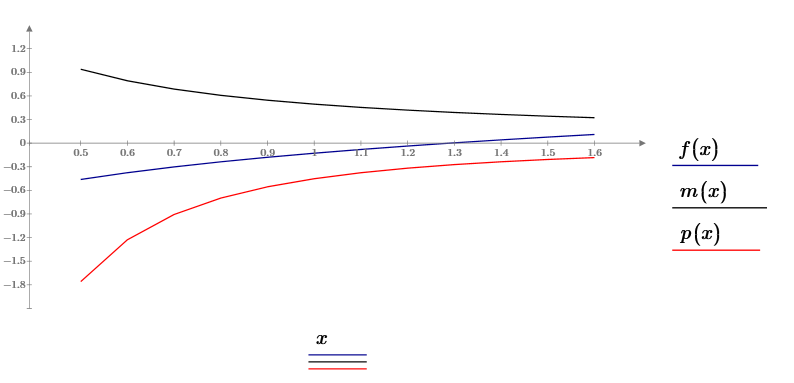
Далее для приближенного вычисления применим метод хорд и касательных

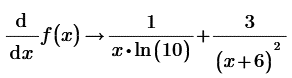
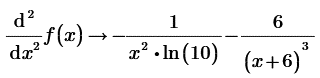
Возьмем отрезок равный единице в месте пересечения только нашей функции с осью Х

Определим где касательная, а где хорда

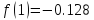– Хорда

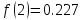– Касательная

Шаг 1:

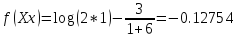
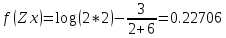
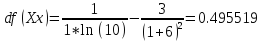
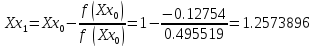
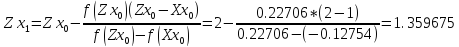
Шаг 2:

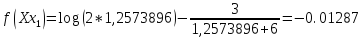
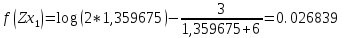
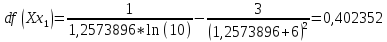
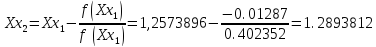
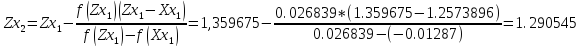
Подставим данные в таблицу Excel:

i	Xx	Zx	F(x)	F(z)	dF(x)	E
0	1	2	-0,12754	0,22706	0,495519	1
1	1,257389606	1,359675	-0,01287	0,026839	0,402352	0,102285861
2	1,289381233	1,290545	-0,00015	0,000311	0,393284	0,001163697
3	1,289753041	1,289753	-1,9E-08	4,07E-08	0,393181	0,0000001522
Корень	1,289753117

Вычислим полученную погрешность:

Полученный результат 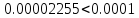- точность достигнута.

Уравнение решено.

ЗАДАЧА № 4

Найти численное решение задачи Коши для данного дифференциального

уравнения и начального условия на отрезке с шагом 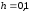методом Рунге – Кутта 4-го порядка.

Дифференциальное уравнение:

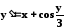
Начальное условие:

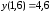
Отрезок: [1.6; 2.6]