Краткая теоретическая часть

Метод Рунге-Кутты используют для расчета стандартных моделей достаточно часто, так как при небольшом объеме вычислений он обладает точностью метода Ο⁴(h).

Для построения разностной схемы интегрирования воспользуемся разложением функции

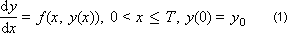
в ряд Тейлора:

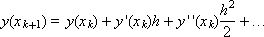
Заменим вторую производную в этом разложении выражением

где

Причем Δx подбирается из условия достижения наибольшей точности записанного выражения. Для дальнейших выкладок произведем замену величины «y с тильдой» разложением в ряд Тейлора:

Для исходного уравнения (1) построим вычислительную схему:

которую преобразуем к виду:

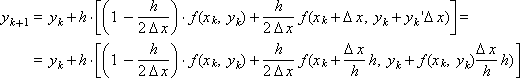
Введем следующие обозначения:

Эти обозначения позволяют записать предыдущее выражение в форме:

Очевидно, что все введенные коэффициенты зависят от величины Δx и могут быть определены через коэффициент α, который в этом случае играет роль параметра:

Окончательно схема Рунге-Кутты принимает вид:

Та же схема в форме разностного аналога уравнения (1):

При α = 0 получаем как частный случай уже известную схему Эйлера:

При α = 1:

При α = 1 проведение расчетов на очередном шаге интегрирования можно рассматривать как последовательность нижеследующих операций.

1. Вычисляется выражение, представляющее собой полушаг интегрирования по схеме Эйлера, то есть определяется приближенное значение искомой функции в точке x_k + h/2:

2. Для той же промежуточной точки находится приближенное значение производной:

3. Определяется уточненное значение функции в конечной точке всего шага, причем по схеме Эйлера с вычисленным на предыдущем шаге значением производной:

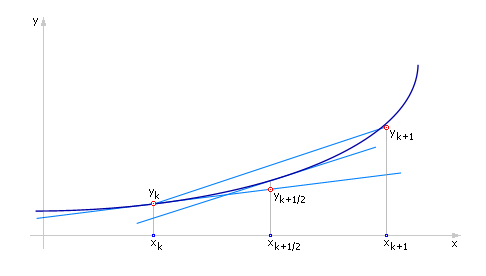
Геометрические построения (см. рис. 15.1) показывают, что получаемое в такой последовательности решение лежит «ближе» к истинному, чем вычисляемое по схеме Эйлера, то есть следует ожидать более высокой точности решения, получаемого методом Рунге-Кутты. Ранее мы назвали эту схему «модифицированным методом Эйлера».

Рис. 1.1. Иллюстрация расчета на шаге методом Рунге-Кутты при значении параметра α = 1

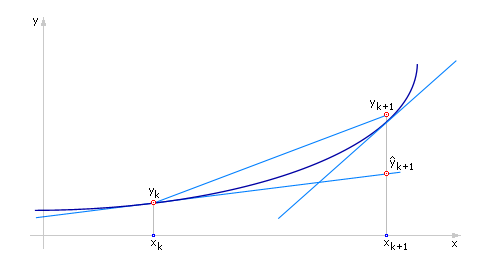
Теперь рассмотрим схему при α = 0.5 (геометрическая интерпретация результата приведена на рис. 1.2).

1. Выполняется полный шаг метода Эйлера с целью определения приближенного значения искомой функции на конце отрезка интегрирования:

2. Для этой же точки вычисляется приближенное значение производной:

3. Находится среднее значение двух производных, определенных на концах отрезка:

4. Вычисляется значение искомой функции в конечной точке всего шага по схеме Эйлера с усредненным значением производной:

Рис. 1.2. Иллюстрация расчета на шаге методом Рунге-Кутты при значении параметра α = 0.5

Иногда получающееся выражение называют схемой (методом) Эйлера-Коши. Геометрически понятно, что получаемый указанным способом результат также должен быть «ближе» к истинному решению, чем получаемый по схеме Эйлера.

Решение

Дифференциальное уравнение:

Начальное условие:

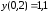
Отрезок: [0,2; 1,2]

Шаг:

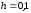
Шаг 1

x₀=0.2; y₀=1.1;

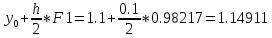
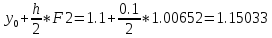
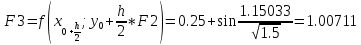
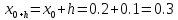
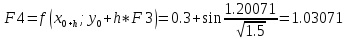
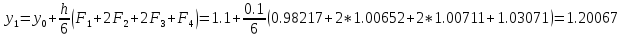
Шаг 2

x₁=0.3; y₁=1.20067;

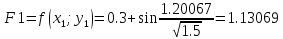
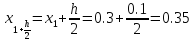
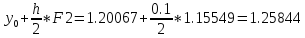
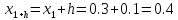
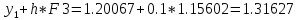
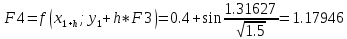
Расчет производим, таким образом, до значения Х₁₀=2,6 с помощью Excel.

В первой части таблицы приведены расчеты с шагом 0,1, а во второй части с шагом 0,2, а также погрешность двойного расчета.

k	x	y	F1	F2	F3	F4	Xk+h/2	Yk+h/2*F1	Yk+h/2*F2	Xk+h	Yk+h*F3	h
0	0,2	1,1	0,982173	1,006521	1,007108	1,030707	0,25	1,149109	1,150326	0,3	1,200711	0,1
1	0,3	1,200669	1,130688	1,155493	1,156017	1,179462	0,35	1,257203	1,258444	0,4	1,316271
2	0,4	1,316222	1,279443	1,303095	1,30351	1,325033	0,45	1,380194	1,381377	0,5	1,446573
3	0,5	1,446517	1,425015	1,445541	1,445813	1,463324	0,55	1,517767	1,518794	0,6	1,591098
4	0,6	1,591034	1,56331	1,578466	1,578594	1,589817	0,65	1,6692	1,669957	0,7	1,748893
5	0,7	1,748821	1,689809	1,69727	1,697293	1,699991	0,75	1,833312	1,833685	0,8	1,918551
6	0,8	1,91847	1,79999	1,797613	1,797619	1,789878	0,85	2,00847	2,008351	0,9	2,098232
7	0,9	2,098142	1,889888	1,87601	1,876133	1,856652	0,95	2,192637	2,191943	1	2,285756
8	1	2,285656	1,956676	1,930392	1,930785	1,899102	1,05	2,38349	2,382176	1,1	2,478735
9	1,1	2,478625	1,999141	1,960469	1,961272	1,917851	1,15	2,578582	2,576649	1,2	2,674752
10	1,2	2,674633	2,017907	1,967789	1,969098	1,915254	1,25	2,775528	2,773022	1,3	2,871543
k	x	y	F1	F2	F3	F4	Xk+h/2	Yk+h/2*F1	Yk+h/2*F2	Xk+h	Yk+h*F3	h	ε
0	0,2	1,1	0,982173	1,029572	1,031727	1,075576	0,3	1,198217	1,202957	0,4	1,306345	0,2	0
1	0,4	1,306012	1,275444	1,320943	1,322384	1,358672	0,5	1,433556	1,438106	0,6	1,570488		0,010
2	0,6	1,570037	1,558567	1,58697	1,58734	1,59956	0,7	1,725894	1,728734	0,8	1,887505		0,0209
3	0,8	1,886929	1,799546	1,793186	1,793246	1,76569	0,9	2,066883	2,066247	1	2,245578		0,0315
4	1	2,244865	1,965841	1,91201	1,913804	1,839382	1,1	2,44145	2,436066	1,2	2,627626		0,0409
5	1,2	2,62676	2,039766	1,938138	1,94371	1,828362	1,3	2,830737	2,820574	1,4	3,015502		0,0479

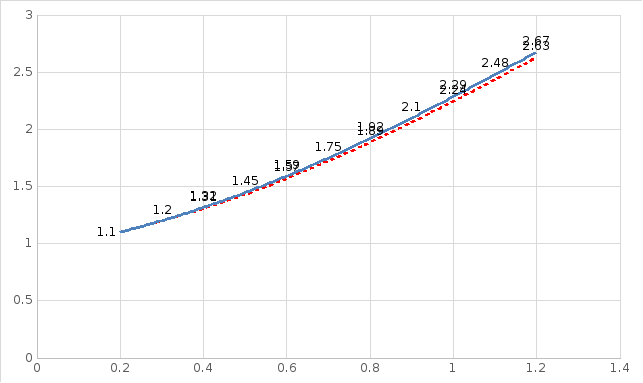
Построим график по вычисленным расчетам: