Задача 1

б) Определить абсолютную погрешность приближенного числа по его относительной погрешности

погрешности;

точное значение

относительная погрешность точного значения

относительная погрешность приближённого значения

абсолютная погрешность приближённого значения

относительная погрешность точного значения

абсолютная погрешность точного значения

=0.0875848

приближённое значение

Абсолютная погрешность приближённого числа

Ответ:

Задача 2

ж) Найти решение СЛАУ АхХ=В , где А- матрица коэффициентов, В- вектор свободных членов, Х- вектор неизвестных, методом Зейделя (заданы матрица А, вектор В, погрешность решения ε, самостоятельно выбрать вектор начального приближения Х0 ). Предварительно для применения этого итерационного метода проверить условие сходимости (диагональное преобладание матрицы А ), в случае его невыполнения следует преобразовать СЛАУ в виду, когда условие сходимости метода выполняется, и эту полученную СЛАУ решить. Для вычисления результата в MathCAD написать функцию пользователя с входными параметрами А, В, Х0, ε, которая выдает в качестве ответа все промежуточные решения (каждой итерации). Полученное приближенное решение сравнить с решением этой СЛАУ в MathCAD вычислительным блоком Given…find (расчет провести в численном виде). Зарисовать блок-схему алгоритма указанного метода решения СЛАУ при условии произвольного количества уравнений (задаются матрица А, вектор В, начальное приближение Х0 и погрешность вычисления ε).

- нумерация массивов начинается с единицы

Преобразование системы Ax=b к виду x=Bx+c, удобному для итераций

Проверка достаточного условия сходимости метода Зейделя

- достаточное условие сходимости выполнено

Метод Зейделя

входные параметры:

B и c - матрица B и вектор правой части c

системы x=Bx+c;

n - порядок матрицы B;

k- число итераций;

x0 - вектор начального приближения.

Функция zeid возвращает двумерный

массив размерности kxn; i-ая строка

которого это i-ое приближение.

Начальное приближение:

Результат работы функции zeid

Блок-схема алгоритма указанного метода решения СЛАУ при условии произвольного количества уравнений

Задача 3

Часть1

б)По заданным узловым значениям исходной функции (векторы и ) осуществить интерполяцию с помощью интерполяционного полинома Ньютона (вид записи - интерполяция вперёд).

Построить в MathCAD в одном графическом шаблоне полученный интерполяционный полином и узловые значения исходной функции.

Зарисовать блок-схему алгоритма, реализующего вычисление значения интерполяционного полинома Ньютона (вперёд) в любом значении аргумента при условии произвольного количества узловых значений исходной функции.

Решение.

Строим интерполяционный полином Ньютона (вид записи – интерполяция вперёд):

.

Разделенными разностями первого порядка, составленными по соседним узлам, называют отношения

По ним можно определить разделенные разности второго порядка

Аналогично определяются разделенные разности более высокого порядка. Например, если известны разделенные разности 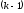-го порядка, то разделенная разность -го порядка определяется как

.

Вычисления в MathCAD:

Построим в MathCAD в одном графическом шаблоне полученный интерполяционный полином и узловые значения исходной функции.

Блок-схема алгоритма, реализующего вычисление значения интерполяционного полинома Ньютона (вперёд) в любом значении аргумента при условии произвольного количества узловых значений исходной функции:

S:=Y[n]

j:=1,k-1

S:=S+P*d[1,k]