Методические указания к выполнению
расчетно-графического задания по теме
"Векторная алгебра и аналитическая геометрия на плоскости и в пространстве".
1. По координатам вершин пирамиды
найти: 1) длину ребра
;
2) угол между ребрами
и
;
3) площадь грани
;
4) объем пирамиды; 5) уравнения прямых
и
;
6) уравнение плоскости
;
7) угол между плоскостями
и
;
8) длину высоты, проведенной из вершины
на грань
.
Сделать чертеж пирамиды в системе
координат.
Решение. 1) Найдем координаты вектора
:
.
Тогда длина этого вектора, т.е. длина
ребра
,
будет равна
.
2) Угол между ребрами
и
равен углу между векторами
и
.
Косинус этого угла найдем по формуле:
.
Вектор
имеет следующие координаты:
.
Тогда
.
Найдем скалярное произведение векторов и :
.
Тогда
.
Отсюда следует, что
тупой угол, равный
.
3) Площадь грани равна половине площади параллелограмма, построенного на векторах и , т.е.
.
Найдем векторное произведение векторов и :
.
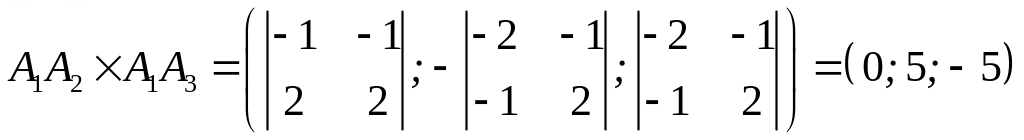Тогда
(кв.ед.).
4) Объем пирамиды равен
объема параллелепипеда, построенного
на векторах
,
,
,
т.е.
.
Вектор
.
Найдем смешанное произведение векторов
.
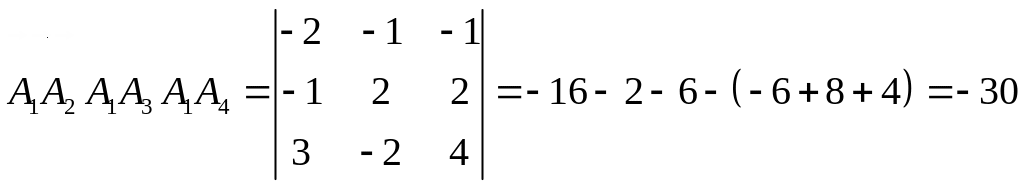Тогда
(куб.ед.).
5) Составим уравнение прямой
.
Она проходит через точку
и ее направляющий вектор
.
Получим
.
Прямая
проходит через точку
и ее направляющий вектор
.
Тогда уравнение этой прямой имеет вид
.
6) Пусть
произвольная точка
плоскости. Плоскость проходит через
точки М,
,
и
,
следовательно, векторы
,
,
компланарны, а значит, их смешанное
произведение равно нулю.
Векторы
,
,
.
Тогда
.
Раскладывая определитель по первой строке, получим
или
.
Отсюда уравнение плоскости
имеет вид:
.
7) Один из углов между плоскостями
и
равен углу между их нормальными векторами,
т.е.
.
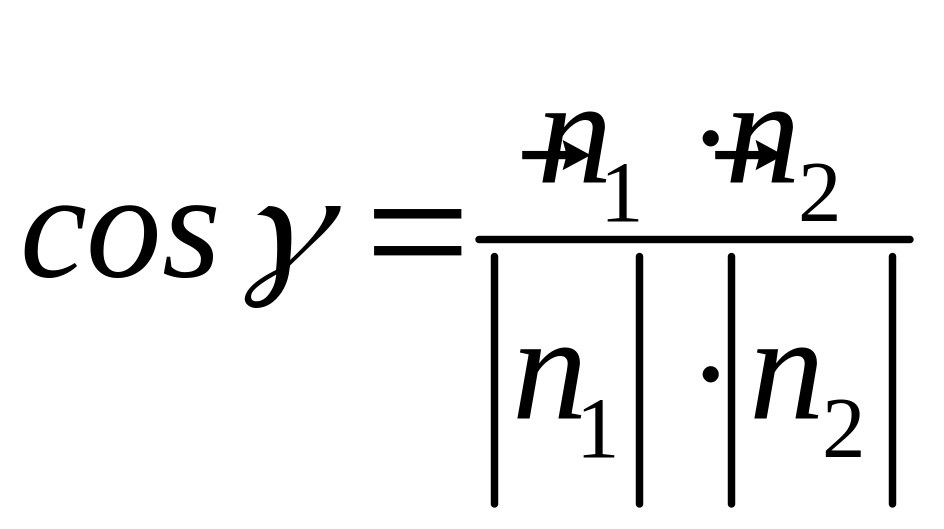Нормальный вектор плоскости
найдем как векторное произведение
векторов
и
:
.
Нормальный вектор плоскости
найдем из уравнения плоскости:
.
Тогда
.
Следовательно,
.
8) Найдем длину высоты, проведенной из
вершины
на грань
.
Она равна расстоянию от точки
до плоскости
:
.
.
9) Чертеж.
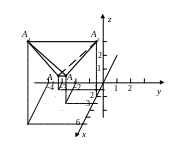
Ответы: 1)
;
2)
;
3)
;
4)
;
5) : ; : ;
6) : ;
7)
;
8)
.
2. Найти точку пересечения прямой и
плоскости:
,
.
Решение. Найдем параметрические уравнения прямой.
,
,
.
Таким образом,
.
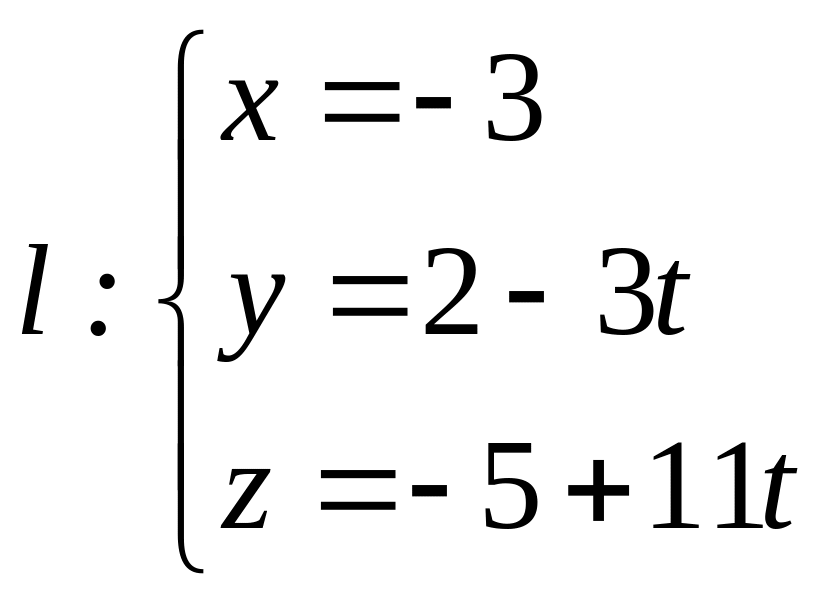Координаты точки пересечения должны удовлетворять и уравнению прямой, и уравнению плоскости, значит, они являются решением системы:
.
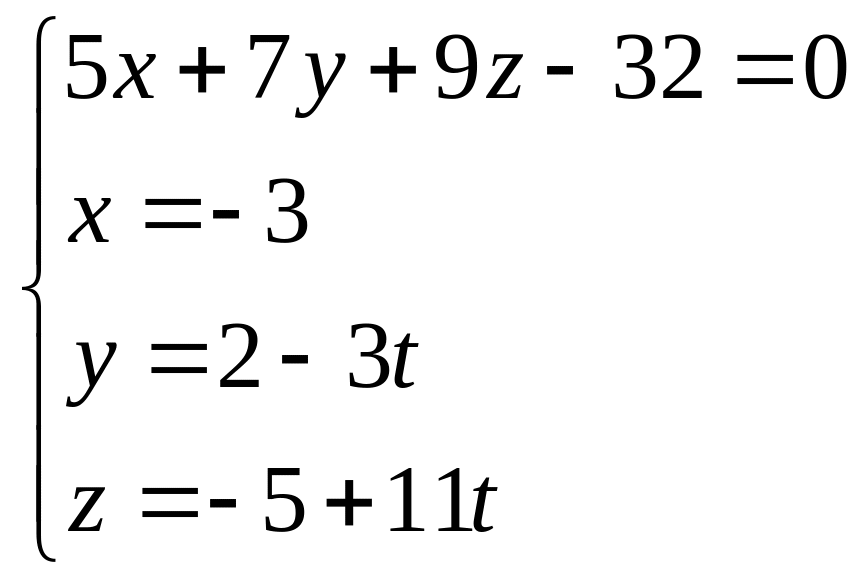Подставляя параметрические уравнения прямой в уравнение плоскости, получим:
,
откуда,
.
Подставляя найденное значение t в уравнение прямой, получим координаты точки пересечения:
.
Ответ:
.
3. Привести уравнение кривой второго
порядка
к каноническому виду. Построить график
кривой.
Решение. Выделим полные квадраты обеих переменных:
,
,
,
.
Получили уравнение гиперболы с центром
в точке
и полуосями
.
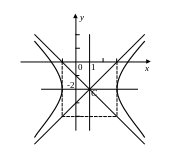
Ответ: .
4. Даны координаты вершин треугольника
:
Требуется: 1) вычислить длину стороны
;
2) составить уравнение стороны
;
3) найти внутренний угол треугольника
при вершине В; 4) составить уравнение
высоты
,
проведенной из вершины А. Сделать
чертеж в системе координат.
Решение. 1)
.
2) Прямая
проходит через точку
и имеет направляющий вектор
.
Найдем уравнение этой прямой:
или
.
Отсюда уравнение прямой имеет вид
.
3) Найдем угол при вершине В, как угол
между векторами
и
.
Векторы
,
.
Тогда
Отсюда
.
4) Уравнение прямой
можно написать, используя уравнение
прямой, проходящей через данную точку,
с заданным угловым коэффициентом:
.
Прямая
перпендикулярна прямой
,
следовательно, их угловые коэффициенты
связаны равенством
.
Из уравнения прямой
получим
.
Тогда
.
Отсюда уравнение прямой
,
проходящей через точку
будет иметь вид:
или
.