Державний університет інформаційно-комунікаціних технолоій

Навчально-науковий інститут Захисту інформації

Кафедра вищої математики

Математичні основи криптографічних перетворень

З В І Т

з лабораторної роботи № 7

Ймовірнісно-статистичні моделі джерел повідомлень

Варіант № 0

Виконав(ла): студент(ка) бсдм(с)(убдм(с)) – 51

Прізвище І.Б.________________________

Дата здачі/захисту____________________

Оцінка______________________________

Перевірив___________________________

2011

Лабораторне заняття № 7

Тема: Ймовірнісно-статистичні моделі джерел повідомлень

Мета роботи: 1. Закріпити відповідний лекційний матеріал.

2. Навчитися обчислювати ентропію випадкової послідовності з дискретним розподілом, визначати залежність ентропії від параметрів розподілу ймовірностей дискретної випадкової величини.

І. Короткі теоретичні відомості (див. лекцію 10)

Джерела дискретних повідомлень та їх ентропійні властивості

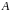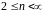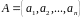Нехай розглядається довільне джерело повідомлень, кожне з яких є послідовністю символів з алфавіту . Якщо алфавіт є скінченною множиною потужності : , то кажуть, що має місце джерело дискретних повідомлень (ДДП). Поява в повідомленні будь-якого символу алфавіту характеризується високою мірою невизначеності. Для математичного опису цієї невизначеності використаємо деяку дискретну ймовірнісну модель

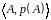
Означення. Ентропією ДДП (або ентропією випадкового символу 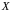) називається величина, яка визначається функціоналом

,

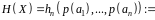
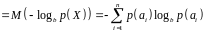де 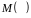– символ математичного сподівання.

Ми будемо користуватися логарифмом за основою 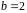і вимірювати ентропію в бітах.

Основні властивості функціонала ентропії.

1. Функціонал ентропії набуває невід’ємних значень: 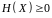, він обертається в 0 тільки для виродженого розподілу:

, , , .

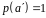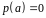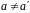(Вироджений розподіл відповідає випадку, коли символ не є випадковим: ).

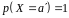2. Ентропія ДДП з алфавітом потужності має максимальне значення

,

яке досягається, якщо дискретний розподіл 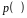– рівномірний, тобто всі значень символів рівноймовірні: .

3. (властивість адитивності) Якщо випадкові символи , 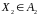повідомлення незалежні, то сумісна ентропія дорівнює сумі ентропій:

.

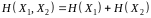4. Додавання до алфавіту символів одного символу з нульовою ймовірністю, а отже, і будь-якої кількості таких символів не змінює ентропії ДДП.

Нехай визначений випадковий -вектор символів 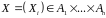з деяким -вимірним дискретним розподілом ймовірностей

,

де . Нехай задано натуральне число , 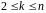і визначений -вимірний дискретний розподіл ймовірностей підвектора 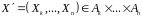за умови, що зафіксований підвектор :

.

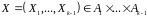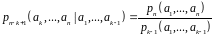(Тут використана формула множення ймовірностей).

Означення. Умовною ентропією підвектору 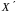за умови, що зафіксований підвектор називається функціонал

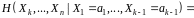
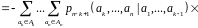
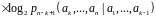
Властивості умовної ентропії.

1. Якщо підвектори випадкових символів , незалежні, то умовна ентропія збігається з безумовною:

2. Для будь-якої послідо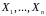вності випадкових символів повідомлення ентропія має властивість ієрархічної адитивності:

.

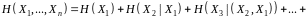
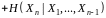Наслідок. Якщо випадкові символи повідомлення незалежні в сукупності, то ентропія має властивість адитивності 3:

3. Умовна ентропія не може перебільшувати безумовну:

.

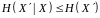Наслідок 1. При додаванні умов умовна ентропія не збільшується:

.

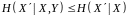Наслідок 2. Ентропія послідовності 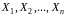випадкових символів повідомлення не перебільшує суми ентропій кожного символу:

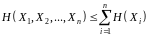
4. При дискретному функціональному перетворенні повідомлення ентропія не збільшується:

,

причому рівність досягається тоді і тільки тоді, коли 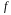– бієкція.

Теорема (єдиності функціоналу ентропії). Нехай для будь-якого натурального числа функція змінних

, ,

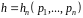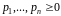неперервна по сукупності аргументів і має наступні три властивості:

а) максимальне значення функції досягається при рівномірному розподілі:

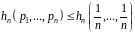
б) ієрархічна аддитивність:

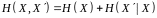
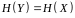
в) додавання до алфавіту, що складається з символів, одного символу

з нульовою ймовірністю (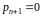 ) не змінює значення ентропії:

.

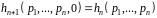Тоді ця функція 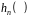необхідно має вигляд:

де 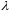– довільна додатна константа.

Нехай розглядається стаціонарний ДДП з деяким алфавітом , що породжує (генерує) 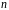-символьні випадкові повідомлення .

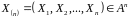Означення. Щільністю ентропії стаціонарного ДДП називається границя

.

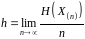якщо вона існує.

За означенням 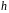є ентропією, що доводиться на один символ і обчислену за нескінченно довгим випадковим повідомленням. Якщо 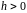, то із збільшенням довжини повідомлення 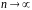ентропія зростає лінійно:

.

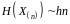Властивості щільності ентропії

1. Для довільного стаціонарного ДДП числова послідовність умовних ентропій , , 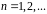має скінченну границю:

.

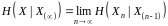2. Для довільного стаціонарного ДДП щільність ентропії існує і збігається з граничним значенням (5):

.

3. Для ентропії довільної дискретної стаціонарної послідовності при збільшенні числа символів справедлива асимптотична рівність

,

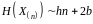де

.

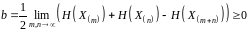В асимптотичній формулі 3. – це -кратна щільність ентропії, 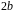– це ентропія, обумовлена граничними ефектами.

Наслідок. Для довільного стаціонарного ДДП без пам’яті асимптотична рівність 3. перетворюється на точну рівність

,

де

–

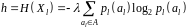ентропія одиничного випадкового символу.

Однорідний ланцюг Маркова як модель джерела дискретних повідомлень

В системах обробки і захисту інформації символи, що утворюють повідомлення звичайно стохастично залежні. Одною з поширених моделей стохастичної залежності символів друкарських текстів, мовних повідомлень і зображень є однорідний ланцюг Маркова (ОЛМ) з дискретним часом і простором станів , .

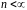Нехай випадкова символьна послідовність, породжена джерелом дискретних повідомлень, є однорідним ланцюгом Маркова. Це означає, що розподіл ймовірностей майбутніх значень (станів) при фіксованих теперішніх і минулих значеннях не залежить від минулих значень:

,

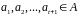, . Відомо також, що усі скінченновимірні розподіли і всі ймовірнісні характеристики ОЛМ повністю виражаються через вектор початкових ймовірностей

, , , .

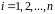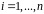і через 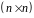-матрицю ймовірностей переходу за один крок:

, , ,

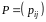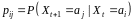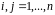Позначимо через 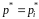, , вектор граничних ймовірностей (стаціонарний розподіл), який є розв’язком системи лінійних алгебраїчних рівнянь:

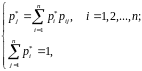
а через

–

ентропію стаціонарного розподілу ймовірностей;

.

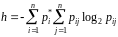Теорема (про ентропію ОЛМ). Якщо випадкова символьна послідовність є ОЛМ із стаціонарним початковим розподілом 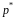і матрицею ймовірностей переходу за один крок, то ентропія повідомлення з символів дорівнює

.

Наслідок. В умовах теореми про ентропію ОЛМ асимптотична рівність перетворюється на точну рівність

,

де

.
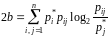