Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Сумский государственный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

lab_23_metod.doc

Скачиваний:

Добавлен:

20.07.2019

Размер:

142.34 Кб

Скачать

☆

1 / 21 2 > Следующая >>>

РОЗВ'ЯЗУВАННЯ РІВНЯНЬ ТА НЕРІВНОСТЕЙ У СИСТЕМІ MAPLE

Основна функція solve()

Для обчислення розв'язку системи алгебраїчних рівнянь у системі Maple використовується стандартна потужна функція solve, яка може бути застосована не тільки до лінійних систем рівнянь, а й до систем нелінійних та окремих рівнянь. Функція solve має такий формат виклику: solve(eqn,var) або solve({eqnl,eqn2,...},{varl,var2,...}), де eqn – рівняння, яке містить змінну; var, {eqnl ,eqn2, ... } – система рівнянь; {varl, var2, ...} – список змінних, відносно яких ця система буде розв'язана.

Характер розв'язків можна змінювати за допомогою глобальних системних змінних:

_EnvExplicit – при значенні true видає розв'язок без використання конструкції RootOf;

_EnvAllSolutions – при значенні true видає всі розв'язки;

_SolutionsMayBeLost – при значенні true видає розв'язок, який при звичайному застосуванні функції solve повертає значення NULL.

Системи лінійних алгебраїчних рівнянь

Для розв'язування систем лінійних алгебраїчних рівнянь призначені потужні матричні методи зі спеціальними функціями. Водночас для розв'язування системи лінійних алгебраїчних рівнянь невисокого порядку можна використовувати функцію solve.

Розглянемо приклади використання функції solve для систем лінійних алгебраїчних рівнянь.

> eq1:=2*x+b*y+2*z=3;

> eq2:=c*x+d*y+4*z=2;

> eq3:=x+2*y+2*z=1;

> simplify(solve({eq1, eq2, eq3}, {x, y, z}));

Приклад можливості обчислення розв'язків неповної системи лінійних алгебраїчних рівнянь (розглядається система трьох рівнянь з чотирма невідомими):

> eqn:={4*x1+7*x2-x3+3*x4=11, -2*x1+2*x2-6*x3+x4=4, x1-3*x1-5*x2-7*x3+5*x4=8};

> solve(eqn, {x1, x2, x4, x4});

Для розв'язування задач лінійної алгебри взагалі, та систем лінійних алгебраїчних рівнянь зокрема у системі Maple передбачений спеціальний пакет LinearAlgebra, в якому серед набору функцій є функція LinearSolve(A, b, method='name_method'), де А – матриця системи рівнянь; b – вектор-стовпець; 'name_method' – один з методів обчислення розв'язків систем рівнянь:

метод LU-декомпозиції (method='LU');

метод QR-декомпозиції (method='QR');

метод декомпозиції Холеського (mehtod='Cholesky');

метод оберненої підстановки (mehtod='subs').

Якщо метод при викликанні функції LinearSolve не зазначається, то використовується метод обернення матриці х = A^-1 b.

Продемонструємо застосування функції LinearSolve для обчислення розв'язку системи лінійних алгебраїчних рівнянь з квадратною матрицею.

> A:=Matrix(4,4, [[1,2,1,4], [2,3,4,5], [3,4,5,6], [4,5,6,10]]);

> b:=Vector (4, [1, 2, 3, Pi]);

> with(LinearAlgebra);

> x:=LinearSolve(A, b);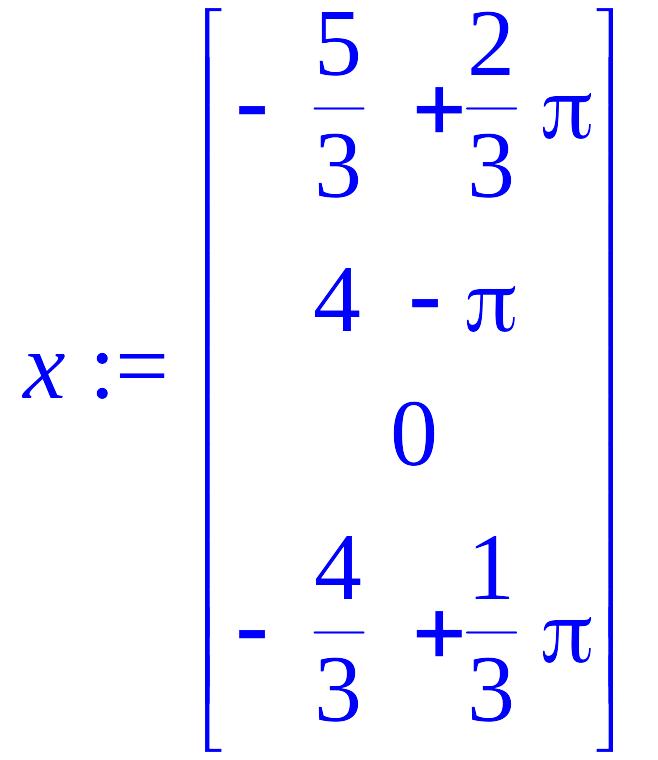

> x1:=LinearSolve(A, b, method='QR');

Перевірку розв'язку можна виконати шляхом обчислення нев'язки розв'язку:

> rx:=A.x-b;

> rx1:=A.x1-b;

Як бачимо, нев'язка в обох випадках дорівнює нуль-вектору. Це свідчить про те, що розв'язок обчислено точно.

Функція LinearSolve здатна обчислювати розв'язки неповних систем рівнянь, в яких кількість рівнянь менша від кількості невідомих. Цю можливість продемонструємо на прикладі. При цьому розв'язок системи рівнянь виражається через вільні системні змінні, кількість яких залежить від рангу матриці.

> A1:=Matrix(3, 4,[[1,2,1,4], [2,3,4,5], [3,4,5,6]]);

> b1:=Vector(3, [1,2,3]);

> x2:=LinearSolve(A1, b1);

Аналогічно функцію LinearSolve можна використати для обчислення розв'язку системи лінійних однорідних систем рівнянь з матрицею, визначник якої дорівнює нулю, що й продемонструємо на прикладі.

> A2:=Matrix(4,4,[[1,2,1,4],[2,3,4,5], [3,4,5,6], [1,1,3,1]]);

> b2:=Vector(4, [0,0,0,0]);

> x2:=LinearSolve(A2, b2, free='s');

Знаходження коренів многочленів

При використанні процедури solve для знаходження коренів многочленів функція знаходить усі корені многочлена – як дійсні, так і комплексні.

>P1:=x->x^4+2*x^3+2*x^2+x+5=0;

> solve(P1(x),x);

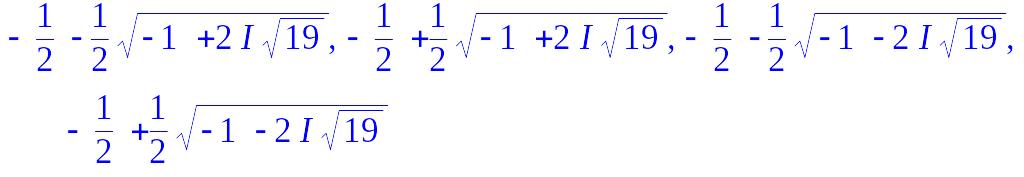
Якщо система Maple не може обчислити корені многочлена в радикалах або таке зображення неможливе, ця система використовує для запису розв'язків функцію RootOf.

Продемонструємо приклад використання функцій solve, RootOf та. Evalf для наближеного обчислення коренів многочлена.

> P2:=x->x^5+3*x^3+32=0;

> solve(P2(x),x);

> evalf(%);

Розв'язування систем алгебраїчних рівнянь

Функцію solve можна використовувати для розв'язування не тільки окремих нелінійних рівнянь, а й систем цих рівнянь. Розглянемо системи рівнянь і способи їх розв'язування в системі Maple:

> exp1:=x^3+y^3=7;

> exp2:=x^3*y^3=-8;

> S:=solve({exp1, exp2}, {x,y});

Серед множини розв'язків системи наведемо лише дійсні розв'язки.

> S[1];

> S[2];

Обчислимо розв'язок.

> exp3:=y^2-x=5;

> exp4:=1/(y-1)-1/(y+1)=1/x;

> S1:=solve({exp3, exp4}, {x, y});

> eval({exp3, exp4}, S1[1]);

> eval({exp3, exp4}, S1[2]);

Розв'язування тригонометричних рівнянь

Тригонометричні рівняння розв'язуються за допомогою звичайної процедури solve з урахуванням тієї особливості, що, як правило, тригонометричні рівняння мають зліченну кількість розв'язків, а процедура solve видає лише один корінь рівняння, який лежить на проміжку [0,2]. Для обчислення всіх розв'язків тригонометричного рівняння необхідно задавати значення глобальної змінної _EnvAllSolutions:=true.

> solve(sin(x)=sqrt(3)/2,x);