
Определитель произведения матриц.
Лемма.
Если
- элементарная матрица, того же порядка,
что и квадратная матрица
,
то
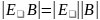 и
и
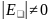 .
.
Доказательство.
Всякая элементарная матрица – треугольная,
и поэтому ее определитель равен
произведению элементов главной диагонали.
Следовательно,
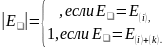 кроме того,
кроме того,
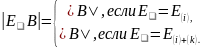
Лемма.
Если
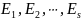 - элементарные матрицы, имеющие тот же
порядок, что и квадратная матрица
,
то
- элементарные матрицы, имеющие тот же
порядок, что и квадратная матрица
,
то
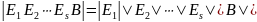 .
.
Доказательство. Самостоятельно, индукцией по .
Следствие.
Если
- элементарные матрицы, имеющие тот же
порядок, то
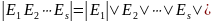 .
.
Теорема.
Определитель произведения двух квадратных
матриц равен произведению их определителей,
т.е.
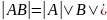 .
.
Доказательство.
Если строки матрицы – линейно независимы, то
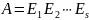 .
Следовательно,
.
Следовательно,
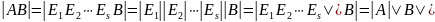 .
.Если строки матрицы линейно зависимы, то с помощью цепочки НЭП матрицу можно привести к ступенчатой матрице , содержащей нулевую строку. Следовательно,
 тогда
тогда
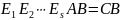 ,
,
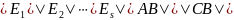 .
Так как
,
а значит и
.
Так как
,
а значит и
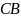 - матрицы с нулевой строкой, то
- матрицы с нулевой строкой, то
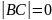 .
Так как
.
Так как
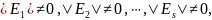 то
то
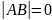 .
Так как строки матрицы
линейно зависимы, то
.
Так как строки матрицы
линейно зависимы, то
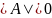 .
Следовательно,
.
Следовательно,
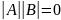 .
Итак,
.
.
Итак,
.
Необходимые и достаточные условия
равенства нулю определителя.
Теорема. Определитель квадратной матрицы равен нулю тогда и только тогда, когда строки (столбцы) матрицы линейно зависимы.
Доказательство.
Пусть
– квадратная матрица порядка
.
Покажем, что если строки матрицы
линейно независимы, ее определитель не
равен нулю. В самом деле, если строки
матрицы
линейно независимы, то ее можно представить
в виде произведения элементарных матриц,
т.е.
 ,
тогда
,
тогда
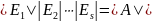 ,
из того, что определитель каждой
элементарной матрицы не равен нулю,
следует, что определитель матрицы
не равен нулю. Таким образом, если
определитель матрицы равен нулю, то
строки матрицы
линейно зависимы. (свойство контрапозиции).
,
из того, что определитель каждой
элементарной матрицы не равен нулю,
следует, что определитель матрицы
не равен нулю. Таким образом, если
определитель матрицы равен нулю, то
строки матрицы
линейно зависимы. (свойство контрапозиции).
Докажем обратное утверждение. Если строки матрицы линейно зависимы, то ее определитель равен нулю. В самом деле, в этом случае одна из строк матрицы является линейной комбинацией других строк, а значит ее определитель равен нулю.
Теорема. Для любой квадратной матрицы равносильны следующие утверждения:
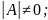
Строки (столбцы) матрицы линейно независимы;
Матрица обратима.
Теоремы о матрицах.
(Лемма 23.)
Теорема о ранге матрицы. Ранг ненулевой матрицы равен наибольшему из порядков ненулевых миноров матрицы.
Доказательство.
Пусть
- ненулевая матрица и
.
Тогда ее ранг
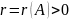 .
Докажем, что матрица
имеет хотя бы один ненулевой минор
порядка
.
Докажем, что матрица
имеет хотя бы один ненулевой минор
порядка
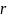 .
Так как
,
то матрица
имеет
линейно независимых строк. Пусть
- подматрица матрицы
,
состоящая из
линейно независимых строк
.
Так как
,
то матрица
имеет
линейно независимых строк. Пусть
- подматрица матрицы
,
состоящая из
линейно независимых строк
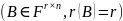 .
Так как ранг матрицы
равен
,
то матрица
содержит
линейно независимых столбцов. Составим
из них матрицу
.
Тогда
.
Так как ранг матрицы
равен
,
то матрица
содержит
линейно независимых столбцов. Составим
из них матрицу
.
Тогда
 .
Получили матрицу, определитель которой
не равен нулю. Таким образом,
.
Получили матрицу, определитель которой
не равен нулю. Таким образом,
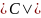 - ненулевой минор
-го
порядка матрицы
.
- ненулевой минор
-го
порядка матрицы
.
Поскольку
любые
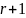 строк матрицы
- линейно зависимы, то все миноры порядка
больше, чем
равны нулю.
строк матрицы
- линейно зависимы, то все миноры порядка
больше, чем
равны нулю.
Определение.
Присоединенной для матрицы
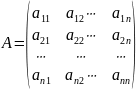 называется матрица
называется матрица
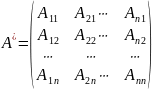 .
.
Присоединенная
матрица обладает следующим свойством:
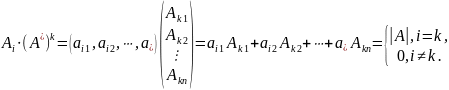
Поэтому,
 .
Следовательно,
.
Следовательно,
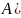 ,
если
,
если
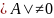 .
.
Аналогично, , если .
Полученные
равенства показывают, что матрицы
и
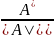 - взаимно обратные. Таким образом,
доказана следующая теорема.
- взаимно обратные. Таким образом,
доказана следующая теорема.
Теорема.
Если определитель квадратной матрицы
не равен нулю, то матрица
обратима и
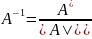 .
.
Правило Крамера.
Рассмотрим
систему n
линейных уравнений с n
неизвестными
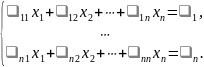 над полем
.
Обозначим через
основную матрицу этой системы
.
над полем
.
Обозначим через
основную матрицу этой системы
.
Теорема. Если , то система линейных уравнений имеет единственное решение, выраженное формулами:
Доказательство.
Полагая
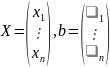 запишем систему в виде матричного
уравнения:
запишем систему в виде матричного
уравнения:
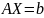 .
Так как
,
то строки матрицы
линейно независимы, следовательно,
система имеет единственное решение
.
Так как
,
то строки матрицы
линейно независимы, следовательно,
система имеет единственное решение
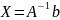 .
Отсюда, по формуле обратной матрицы:
.
Отсюда, по формуле обратной матрицы:
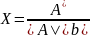 .
Произведя умножение матриц, получим
.
.
Произведя умножение матриц, получим
.
Полученные формулы называются формулами Крамера, а теорема – правилом Крамера.
Обозначим
через
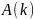 матрицу, получающуюся из матрицы
заменой
-го
столбца, столбцом
матрицу, получающуюся из матрицы
заменой
-го
столбца, столбцом
 ,
тогда можно сформулировать правило
Крамера в следующем виде:
,
тогда можно сформулировать правило
Крамера в следующем виде:
Теорема. Если , то система линейных уравнений имеет единственное решение, выраженное формулами: .
Условия, при которых система n линейных однородных уравнений с n неизвестными имеет ненулевое решение.
Определение.
Система
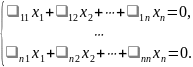 называется системой n
линейных однородных уравнений с n
неизвестными.
называется системой n
линейных однородных уравнений с n
неизвестными.
Теорема. Система n линейных однородных уравнений с n неизвестными имеет ненулевое решение тогда и только тогда, когда, когда определитель основной матрицы системы равен нулю.
Доказательство. Пусть дана система n линейных однородных уравнений с n неизвестными и – основная матрица этой системы.
Система
имеет ненулевые решения в том и только
в том случае, когда столбцы матрицы
линейно зависимы. Столбцы матрицы
линейно зависимы тогда и только тогда,
когда
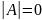 .
.
Следовательно, система имеет ненулевые решения тогда и только тогда, когда .
Решение системы n линейных уравнений
с n неизвестными в матричной форме.
(Лемма 24.)
Определение. Системой n линейных уравнений и n неизвестными называется система вида:
 над полем
.
над полем
.
Введем
обозначения:
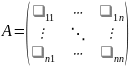 ,
,
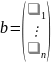 ,
,
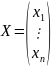 ,
то систему можно записать в виде
матричного уравнения:
.
,
то систему можно записать в виде
матричного уравнения:
.
Полученное уравнение называется матричной формой системы уравнений.
Теорема.
Если строки матрицы
линейно независимы, то вектор
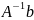 является единственным решением уравнения
.
является единственным решением уравнения
.
Системы линейных уравнений.
Определение.
Системой
линейных уравнений
над полем
с
переменными
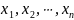 называется система вида
называется система вида
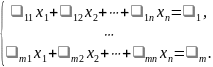 .
.
Определение.
Вектор
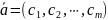 называется решением
системы (*) если
верны равенства
называется решением
системы (*) если
верны равенства
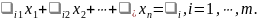
Определение. Система (*) называется совместной, если она имеет, хотя бы одно решение. Система (*) называется несовместной, если она не имеет ни одного решения.
Определение. Совместная система (*) называется определенной, если она имеет единственной решение. Совместная система (*) называется неопределенной, если она имеет множество решений.
Для
системы (*) введем следующие обозначения:
- основная матрица системы,
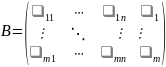 - расширенная матрица системы,
- столбец свободных коэффициентов,
- столбец неизвестных.
- расширенная матрица системы,
- столбец свободных коэффициентов,
- столбец неизвестных.
Теорема. (Кронеккера-Капелли). Система (*) совместна тогда и только тогда, когда ранги расширенной и основной матриц системы равны. Совместная система определена тогда и только тогда, когда ранг основной матрицы равен числу неизвестных.
Доказательство.
Если ранги основной и расширенной матриц
не равны, то в процессе приведения
расширенной матрицы к ступенчатому
виду будет получена строка
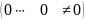 ,
которой соответствует уравнение
,
которой соответствует уравнение
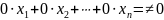 ,
которое не имеет решений, а значит и вся
система уравнений не имеет решений,
т.е. она несовместна.
,
которое не имеет решений, а значит и вся
система уравнений не имеет решений,
т.е. она несовместна.
Если ранги основной и расширенной матриц равны, и совпадают с числом неизвестных, то в процессе приведения расширенной матрицы к ступенчатому виду будет получена матрица
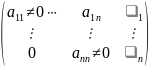 ,
,
которой соответствует система уравнений:
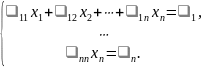
из
последнего уравнения системы найдем
значение
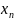 и подставим его значение вовсе остальные
уравнения. Из предпоследнего уравнения
найдем значение
и подставим его значение вовсе остальные
уравнения. Из предпоследнего уравнения
найдем значение
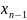 ,
и т.д. из первого уравнения найдем
значение
,
и т.д. из первого уравнения найдем
значение
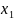 .
В итоге получим единственное решение
системы.
.
В итоге получим единственное решение
системы.
Если
ранги основной и расширенной матриц
совпадают
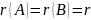 и меньше числа неизвестных
и меньше числа неизвестных
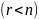 ,
тогда в процессе приведения расширенной
матрицы к ступенчатому виду будет
получена матрица
,
тогда в процессе приведения расширенной
матрицы к ступенчатому виду будет
получена матрица
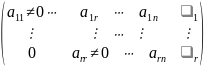 ,
,
которой соответствует система уравнений:
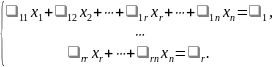
Преобразуем полученную систему к следующему виду:
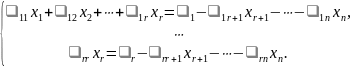
Выразим
из последнего уравнения значение
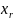 и подставим его значение во все остальные
уравнения системы. Выразим из предпоследнего
уравнения системы значение
и подставим его значение во все остальные
уравнения системы. Выразим из предпоследнего
уравнения системы значение
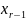 ,
и т.д. найдем выражения для всех переменных
,
и т.д. найдем выражения для всех переменных
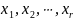 через переменные
через переменные
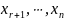 .
Если в качестве значений переменных
выбирать любые значения из поля
,
то можно вычислить соответствующие
значения переменных
,
в итоге будет найдено конкретное решение
системы. Так как таких наборов значений
– множество, то система будет иметь
множество решений, т.е. неопределенная.
.
Если в качестве значений переменных
выбирать любые значения из поля
,
то можно вычислить соответствующие
значения переменных
,
в итоге будет найдено конкретное решение
системы. Так как таких наборов значений
– множество, то система будет иметь
множество решений, т.е. неопределенная.
Определение. Переменные из доказательства теоремы называются свободными, их количество равно разности числа переменных системы и ранга расширенной матрицы, а переменные называются зависимыми.
Определение. Множество всех решение системы называется общим решением системы.
Пример: Решить систему уравнений методом последовательного исключения переменных (методом Гаусса).
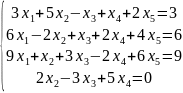
Решение.
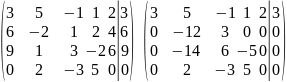
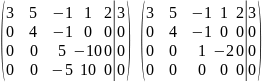 .
.
Составим систему уравнений:
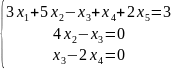 ,
так как число переменных 5, а количество
уравнений в полученной системе 3, то
можно выбрать 5-3=2 свободных переменных
,
так как число переменных 5, а количество
уравнений в полученной системе 3, то
можно выбрать 5-3=2 свободных переменных
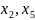 .
Тогда получим:
.
Тогда получим:
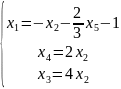 .
.
Таким образом, общее решение системы уравнений имеет вид:
 .
.
Однородные системы. Фундаментальный набор решений однородной системы. Пространство решений однородной системы.
(Лемма 25.)
Определение. Однородной системой линейных уравнений над полем с переменными называется система вида
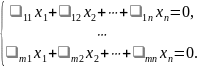
Лемма. Однородная система является совместной.
Доказательство.
Так как нулевой вектор
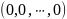 является решением системы, то система
– совместная.
является решением системы, то система
– совместная.
Определение. Если система имеет множество решений, то придавая свободным переменным произвольные ненулевые значения из поля , такие, чтобы векторы решений являлись линейно независимыми, получим множество линейно независимых решений однородной системы, которое называется фундаментальным набором.
Теорема. Множество решений однородной системы является векторным пространством.
Доказательство. Так как является решением системы, то множество решений не является пустым. Докажем, что оно образует векторное пространство, с помощью критерия.
Пусть
 - два решения однородной системы, тогда
непосредственной проверкой, нетрудно
показать, что
- два решения однородной системы, тогда
непосредственной проверкой, нетрудно
показать, что
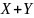 - тоже решение системы.
- тоже решение системы.Пусть
 и
и
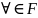 ,
тогда нетрудно показать, что
,
тогда нетрудно показать, что
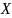 - решение системы.
- решение системы.
Следовательно, множество решений системы – векторное пространство.
Многообразие решений системы линейных уравнений.
Определение. Однородная система
называется соответственной для неоднородной системы
.
Теорема. Множество решений системы линейных уравнений
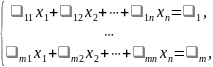
равно сумме пространства решений соответствующей однородной системы и частного решения исходной системы.
Доказательство. Пусть – множество решений системы
,
а
 - сумма пространства решений соответствующей
однородной системы
- сумма пространства решений соответствующей
однородной системы
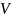 и частного решения исходной системы
и частного решения исходной системы
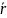 .
.
Если
исходная система несовместна, то она
не имеет ни одного решения, следовательно,
не существует ни одного частного решения,
а значит оба множества являются пустыми,
т.е.
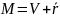 .
.
Пусть
исходная система совместна, и
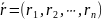 – некоторое частное решение. Покажем
равенство множеств методом встречных
включений.
– некоторое частное решение. Покажем
равенство множеств методом встречных
включений.
Пусть
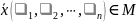 ,
рассмотрим вектор
,
рассмотрим вектор
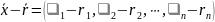 ,
покажем, что он является решением
соответственной однородной системы.
,
покажем, что он является решением
соответственной однородной системы.
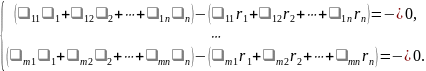
Следовательно,
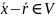 ,
т.е.
,
т.е.
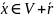 .
.
Пусть
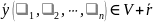 ,
покажем, что
,
покажем, что
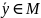 .
Действительно, так как
.
Действительно, так как
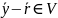 ,
то вектор
,
то вектор
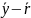 - решение соответствующей однородной
системы уравнений. Тогда
,
- решение соответствующей однородной
системы уравнений. Тогда
,
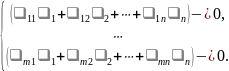 Получили, что
Получили, что
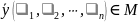 .
.Из 1. и 2. следует, что .
Определение. Множество называется многообразием решений неоднородной системы линейных уравнений.
Пример. Представить общее решение системы через пространство решений соответствующей однородной системы и частное решение исходной системы.
Решение.
Так
как
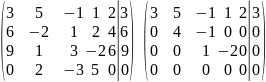 ,
составим соответствующую однородную
систему и найдем её пространство решений:
,
составим соответствующую однородную
систему и найдем её пространство решений:
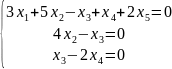 ,
,
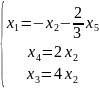 .
.
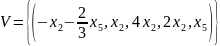 - пространство решений однородной
системы.
- пространство решений однородной
системы.
Для исходной системы найдем частное решение:
,
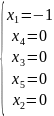 ,
,
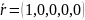 - частное решение исходной системы.
- частное решение исходной системы.
Тогда общее решение исходной системы имеет вид: .
