
Экстремум функций многих переменных.
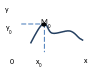
М0(x0;y0) – точка локального максимума функции z= f(x,y), если для любой M(x,y) из окрестности М0(x0;y0) справедливо неравенство f(M0) > f(M).
Для нахождения экстремумов функции необходимо:
1. Нахождения частных производных первого порядка, и приравнивание частной производной к нулю для нахождения стационарных точек.
|
2. Нахождение частных производных второго порядка.
|
∆= AC - B2
Рассмотрим возможные случаи ∆:
∆ > 0 экстремум существует.
A < 0 – max
A > 0 – min
∆ < 0 экстремум не существует.
∆ = 0
Производные высших порядков.
Под
действием линейного оператора
![]() ,
пространство V переходит
в
,
пространство V переходит
в
![]() .
.
![]()
Для множества линейных операторов.

![]()
![]()
Величина более высокого порядка малости.
Т.е.


![]()


Смешанное дифференцирование не зависит от порядка дифференцирования.
П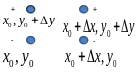 усть
есть некая
усть
есть некая
![]()
Рассмотрим разность разностей.


Т.к.
![]() - одинаковое в обоих случаях, то
- одинаковое в обоих случаях, то
![]() мы
получаем равенство
мы
получаем равенство

Тем самым мы доказали что можно дифференцировать по любой из переменных в смешенном дифференциале.
Ряд и формула Тейлора.
Ряд Тейлора.

Для множества переменных:

Формула Тейлора.
![]()

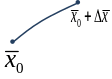
Если во всех точках отрезка соблюдается,
Тогда
получаем
![]()
Теорема о конечном приращении.
Пусть
существует пространство
![]()
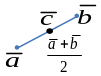

Доказательство.
Пусть

Т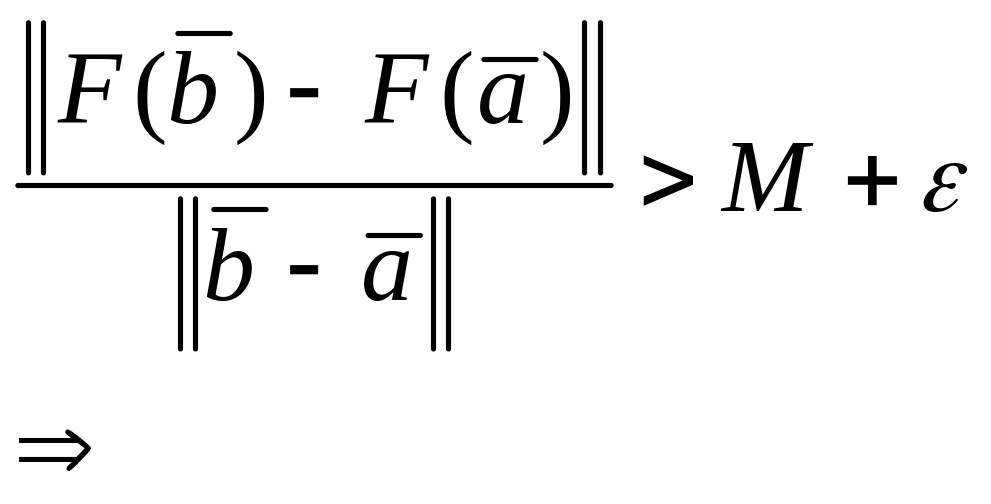 огда
огда


Расстояние между
![]() и
и
![]() - стремится к нулю
- стремится к нулю
![]()

![]()
![]()
18.Приближенный метод определения экстремума.
![]()



Метод наименьших квадратов
 если выбираем параметр а, так что бы
сумма была минимумом.
если выбираем параметр а, так что бы
сумма была минимумом.
Пример:


![]()
Градиентный спуск:
Ч ем
ближе к экстремуму - тем меньше «шаги»
(т.е. градиент)
ем
ближе к экстремуму - тем меньше «шаги»
(т.е. градиент)
Но тут
надо найти
![]() берем
из:
берем
из:
![]()
Эта задача проще Метода наименьших квадратов, тут одна переменная , а не ряд..но считать надо на каждом шаге

Берем другой вектор
 Метод тяжелого шарика (Шар катится
по оврагу, рано или поздно
Метод тяжелого шарика (Шар катится
по оврагу, рано или поздно
остановившись в центре оврага)
Чем
ближе
![]() к единице - тем больше инерция у шарика
к единице - тем больше инерция у шарика
Метод сопряженных градиентов для квадратичной формы
-переменная:
![]()
![]()
![]() (
Не квадратичную форму раскладываем в
ряд Тейлора)
(
Не квадратичную форму раскладываем в
ряд Тейлора)

Экстремум тут находится:

И находим экстремум на каждом шаге.
Метод Ньютона
![]()
![]()
![]() -мало
-мало
![]()


Но
для
![]() -надо
находить обратную матрицу, решая систему
л.у.
-надо
находить обратную матрицу, решая систему
л.у.
Тут сходимость, как в : 2,4,,16,256,,,,
Демпфированный метод Ньютона
Берем:
![]()
![]()
КвазиНьютоновский
Оцениваем :
![]()
Используя
направления, накапливаем
![]() ,
чтобы была ближе к
,
чтобы была ближе к
![]()
Градиент. Производная по направлению. Необходимые условия экстремума.
 - если оператор ограничен.
- если оператор ограничен.

![]() - градиент
- градиент
![]()
![]()
![]()
![]() для получения
для получения
![]() - нужно
- нужно
![]() и (!)
и (!)![]()
![]()
![]()
Если функция дифференцируема, то существует частная производная.
![]()
![]()

![]()
![]() - локальные
- локальные
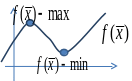
Соответствующая производная должна быть равна 0
![]() равно нулю при любом
равно нулю при любом
![]()
![]() - необходимое условие для локального
экстремума.
- необходимое условие для локального
экстремума.


![]()
Достаточное условие экстремума.



![]() >0
>0
В достаточно малой окружности (области).


![]()
![]()
![]()
Условный экстремум.
 - дифференцируемые функции.
- дифференцируемые функции.

 меняет знак
меняет знак
![]()

![]() -
если будет >0 или <0, то мы не получим
0.
-
если будет >0 или <0, то мы не получим
0.
![]()
![]() и
и
![]() Тогда мы имеем
Тогда мы имеем

![]() =
=
15.Т.Вейерштрасса для функции многих переменных
![]()
![]() (
(![]() -компакт
т.е. замкнутая и ограниченная область)
-компакт
т.е. замкнутая и ограниченная область)
![]() достигает на этом компакте своего
наибольшего и наименьшего значения
достигает на этом компакте своего
наибольшего и наименьшего значения
![]() :
:![]() =inf
;
=inf
;
![]() =sup
=sup
![]() :
:![]() ⇒
⇒![]() A=inf
,
B=sup
A=inf
,
B=sup
![]()
![]() =sup
=sup
![]()
![]()
![]()
![]()
![]()
![]() :
:![]()
![]()
![]() :
:![]()



![]()
![]()
![]()
![]()
10.Условие Коши-Римана
![]()
![]()



![]()
Раскладываем и сравниваем:
![]()
![]()
![]() =
=![]()
![]()

 -----Условие
Коши-Римана
-----Условие
Коши-Римана
9 .Достаточные
условия дифференцируемости
.Достаточные
условия дифференцируемости
![]()

Функция меняет значение от 1,0…





Вдоль любого направления есть производная, равная «0»(т.к. функция равна нулю)=> имеет производные во всех направлениях, и частную в нуле.
Но она не будет дифференцируема, т.к. она не будет непрерывная, потому что в любой окрестности «0» она равна то «0», то «1» (в нуле не имеет предела)
Доказываем для f(x,y,z)
![]()
![]() (предполагаем
непрерывность Частных Производных в
окрестности точки)
(предполагаем
непрерывность Частных Производных в
окрестности точки)

Все это в силу непрерывности Частных Производных( и => так же для сколь угодно много слагаемых)
1.Метрические пространства. Примеры.
Определение
![]() M – множество
M – множество
![]()
![]() -
операция 2-ух переменных
-
операция 2-ух переменных
10
![]() обращается в ноль при совпадении двух
элементов
обращается в ноль при совпадении двух
элементов
20 симметричность операции
![]()
30 неравенство треугольника
![]()
def метрика (расстояние)
Примеры:
10
![]()
![]()
20

30
![]()

 Эвклидова метрика (норма совпадает с
разностью вектора)
Эвклидова метрика (норма совпадает с
разностью вектора)
40
![]()
![]()
f-не прерывно на отрезке [a,b]
пространство функции не прерывно на отрезке [a,b]

2.Сходимость метрического пространства.
Свойства метрического пространства
Определение:
10 М- множество
![]() -
метрика на М
-
метрика на М
(М, )def метрическое пространство (МП)
20
![]()
![]()
Пространство сходится по метрике этого пространства, если расстояние между ними стремится к нулю.
![]() (по
метрике)
(по
метрике)
![]()
![]()
30 Последовательность называется фундаментальной в данной метрике.
![]() def
фундаментальная последовательность
def
фундаментальная последовательность
![]()
![]()
Замечание:
10 Любая сходящаяся последовательность будет являться фундаментальной
![]() -
сходится в М
-
сходится в М
![]() -
фундаментальная
-
фундаментальная
Доказательство:
Пусть
![]()
![]()
![]()
![]()
Последовательность фундаментальна
20 Обратно не верно.
Если последовательность фундаментальна, она не обязательно будет сходиться.
![]()
![]() -фундаментальна
-фундаментальна
Но не является сходящейся в М
Рассмотрим метрическое пространство.
Любая фундаментальная последовательность будет сходящейся.
Такое пространство называется полным.
![]() -
МП
-
МП
Пусть
![]()
-
фундаментальна
![]()
def ПМП
Примеры:
10
![]() -
ПМП
-
ПМП
20 пространство непрерывной функции
Sup разности – метрика
![]() - ПМП
- ПМП
Определение: есть МП
- МП
Есть отображение МП в себя (оператор)
![]() (оператор)
(оператор)
10
F
– непрерывно в
![]()
![]()
4.Принцип сжимающихся отображений.
20
![]() сжимающее отображение
сжимающее отображение
Сжимающий оператор, если существует const такая, что для любых двух элементов выполняется следующее:
![]()
![]()
Замечание.
Любое сжимающее отображение непрерывно в любой точки
Сжимающее
отображение непрерывно
![]()
Пусть
![]()
![]()
![]()
Определение
- МП
![]()
![]() неподвижная
точка
неподвижная
точка
![]()
Теорема.
Принцип сжимающих отображений
- ПМП
сжимающий оператор
Тогда:
![]() - неподвижная точка F
(единственная точка)
- неподвижная точка F
(единственная точка)
Доказательство
Пусть неподвижная точка, 2-е , они совпадают
Единственность:
пусть
![]()
![]()
![]()
![]()
![]()
Отображение сжимающее, поэтому
Существование
Пусть
Построим последовательность, которая сходится в неподвижной точки.
Построим
![]()
Каждая последующая является образам предыдущей
2 соседних индекса
![]()
Докажем, что последовательность фундаментальна
![]()
![]()
Отображение сжимающее.
Возьмем 2 различных индекса.
![]()
![]() между
ними много индексов
между
ними много индексов

![]() -геометрическая
прогрессия
-геометрическая
прогрессия
![]() -геометрическая
прогрессия
-геометрическая
прогрессия
![]() -
бесконечно убывающая геометрическая
прогрессия
-
бесконечно убывающая геометрическая
прогрессия
Расстояние между соседними стремится к 0
-фундаментальная последовательность
![]() -ПМП
-ПМП
![]()
![]() (неподвижная
точка)
(неподвижная
точка)
Докажем:
![]() -
неподвижная точка F
-
неподвижная точка F
![]()
Применим неравенство треугольника
![]()
![]() -
образ предыдущего
-
образ предыдущего
Используем сжимающее отображение
![]()
Последовательность
сходится к
![]() ,
поэтому можно ее сделать бесконечно
малым.
,
поэтому можно ее сделать бесконечно
малым.
![]()
Из этого следует, что расстояние 0
![]()
Из этого следует, что совпадают
3. Полнота, неполнота, пополнение (пространств)
Билет № 2 пункт 30
Теорема.
(Полнота пространства непрерывных функций)
Полнота
![]()
![]() -
ПМП
-
ПМП
Доказательство: фундаментальные последовательности сходятся
![]()
![]()
Пускай последовательность фундаментальна
Определить фундаментальность последовательности
![]()
![]()
Для каждого x числа последовательность фундаментальна
![]() - фундаментальная
последовательность
- фундаментальная
последовательность
По критерию Коши это сходящаяся последовательность
![]() - сходится (
- сходится (![]() )
)
![]()
![]()
Применили
к пределу при m![]() ,
так как x
фиксирован
,
так как x
фиксирован
![]()
Получили подточенную последовательность
![]()
(!) докажем непрерывность
(!)![]()
Была
предельная сходимость, значит
![]() равномерно сходится к
равномерно сходится к
![]()
![]()
![]() значит пространство
полное
значит пространство
полное
![]()
![]()
![]()
 - расстояние между 2 точками
- расстояние между 2 точками
![]()
![]()
![]() определение
предела последовательности
определение
предела последовательности
![]()
![]()
![]()
![]()

![]()
![]()








![]()
![]()
Для эти метрики эквивалентны
Окрестность нуля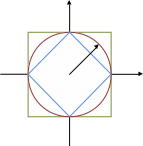



![]() вектор сходится
к 0
вектор сходится
к 0
Если
- окрестности принадлежит
,
то она принадлежит и
![]()
Если попало во внутренний кружок, тогда попало и в ромб и выполняется:
![]()
Если сходимость в одной метрики, то сходимость в другой.
![]()
В - окрестность одну вкладывается - окрестность другая.
Доказательство:

![]()
![]()
![]()
Раз для всех i выполняется, значит и для max выполняется.
Наоборот:
![]()

- полное пространство, любая фундаментальная последовательность сходится.
Фундаментальность: последовательность Коши
![]()
![]()
![]() -член
последовательности
-член
последовательности
![]() -
координаты
-
координаты
![]()
![]()
![]()
Последовательность для всех i является фундаментальной.
![]()
![]()
![]()
Если сходимость векторов, номер должен быть общим.

Меняется по всему промежутку.
Относительно метрике пространство
![]() не является полным
относительно
,
не является полным
относительно
,
![]() последовательность
является фундаментальной и не сходится.
последовательность
является фундаментальной и не сходится.
1
1
1/n
1/m







t
fn(t)
![]()
![]() эта последовательность
фундаментальна
эта последовательность
фундаментальна
0 <t<1
<t<1
f(t0)







Фиксируем t0
Для всех t окрестности
![]()
![]()
![]() - метрика 1
- метрика 1

![]()
Последовательность функции будет не сходиться к функции не прерывной.
Не будет не прерывной, следовательно, пространство не является полным.
1
-1
1
-1
1/n
-1/n






![]()
Д ля
любого отрезка
ля
любого отрезка
1
-1




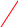


Функции не прерывны. Последовательности фундаментальны. Не является полным относительно метрике .


