
Определитель n-ого порядка.
Определителем квадратной матрицы порядка n называется число:

![]()
Свойства определителей:
Определитель транспонированной матрицы равен определителю исходной матрицы.
Если в определителе какие-либо две строки (столбца) равны между собой, то такой определитель равен 0.
Общий множитель всех элементов какой-либо строки (или столбца) можно выносить за знак определителя.
Если поменять в определителе местами какие-либо две строки (столбца), то определитель меняет знак.
Если все элементы какой-либо строки (столбца) определителя равны 0, то такой определитель равен 0.
Если к элементам какой-либо строки (столбца) определителя прибавить соответствующие элементы другой строки (столбца) этого же определителя, умноженные на одно и то же число, то определитель не изменяется.
Миноры, алгебраические дополнения матрицы.
Минором Mij, соответствующим данному элементу определителя 3 порядка, называется определитель второго порядка, полученный из матрицы вычеркиванием i-ой строки и j-го столбца. Тогда формулу для вычисления определителя 3 порядка можно переписать в виде:
Если элементы матрицы отметить точками, то получим правило треугольников:
(+) |
(-) |
|
|
Слагаемые со знаком плюс представляют собой произведение элементов определителя, взятых по три так, как указано линией на левой части рисунка, а со знаком минус - на правой части.
Алгебраическим
дополнением элемента ![]() определителя
3-го порядка называется его минор, взятый
со знаком плюс, если (i+j) - четное число,
и со знаком минус, если (i+j) - нечетное
число, т.е.
определителя
3-го порядка называется его минор, взятый
со знаком плюс, если (i+j) - четное число,
и со знаком минус, если (i+j) - нечетное
число, т.е.
![]()
ОБРАТНАЯ МАТРИЦА.
Рассмотрим квадратную матрицу
 .
.
Обозначим =det A.
Квадратная матрица А называется невырожденной, или неособенной, если ее определитель отличен от нуля, и вырожденной, или особенной, если = 0.
Квадратная матрица В называется обратной для квадратной матрицы А того же порядка, если их произведение А В = В А = Е, где Е - единичная матрица того же порядка, что и матрицы А и В.
Теорема. Для того, чтобы матрица А имела обратную, необходимо и достаточно, чтобы ее определитель был отличен от нуля.
Матрица, обратная матрице А, обозначается через А1, так что В = А1. Обратная матрица вычисляется по формуле
 ,
(4.5)
,
(4.5)
где А i j - алгебраические дополнения элементов a i j.
Вычисление обратной матрицы по формуле (4.5) для матриц высокого порядка очень трудоемко, поэтому на практике бывает удобно находить обратную матрицу с помощью метода элементарных преобразований (ЭП). Любую неособенную матрицу А путем ЭП только столбцов (или только строк) можно привести к единичной матрице Е. Если совершенные над матрицей А ЭП в том же порядке применить к единичной матрице Е, то в результате получится обратная матрица. Удобно совершать ЭП над матрицами А и Е одновременно, записывая обе матрицы рядом через черту. Отметим еще раз, что при отыскании канонического вида матрицы с целью нахождения ее ранга можно пользоваться преобразованиями строк и столбцов. Если нужно найти обратную матрицу, в процессе преобразований следует использовать только строки или только столбцы.
Пример
2.10.
Для матрицы
 найти
обратную.
найти
обратную.
Решение.
Находим
сначала детерминант матрицы А
 значит,
обратная матрица существует и мы ее
можем найти по формуле:
значит,
обратная матрица существует и мы ее
можем найти по формуле: 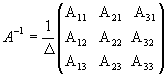 ,
где Аi
j
(i,j=1,2,3) - алгебраические дополнения
элементов аi
j исходной
матрицы.
,
где Аi
j
(i,j=1,2,3) - алгебраические дополнения
элементов аi
j исходной
матрицы.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
откуда
 .
.
Пример
2.11.
Методом элементарных преобразований
найти обратную матрицу для матрицы: А=
 .
.
Решение.
Приписываем
к исходной матрице справа единичную
матрицу того же порядка:
 .
С помощью элементарных
преобразований
столбцов приведем левую “половину” к
единичной, совершая одновременно точно
такие преобразования над правой матрицей.
Для
этого поменяем местами первый и второй
столбцы:
.
С помощью элементарных
преобразований
столбцов приведем левую “половину” к
единичной, совершая одновременно точно
такие преобразования над правой матрицей.
Для
этого поменяем местами первый и второй
столбцы:
 .
К третьему столбцу прибавим первый, а
ко второму - первый, умноженный на -2:
.
К третьему столбцу прибавим первый, а
ко второму - первый, умноженный на -2:
 .
Из первого столбца вычтем удвоенный
второй, а из третьего - умноженный на 6
второй;
.
Из первого столбца вычтем удвоенный
второй, а из третьего - умноженный на 6
второй;
 .
Прибавим третий столбец к первому и
второму:
.
Прибавим третий столбец к первому и
второму:
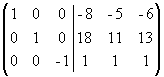 .
Умножим последний столбец на -1:
.
Умножим последний столбец на -1:
 .
Полученная справа от вертикальной черты
квадратная матрица является обратной
к данной матрице А. Итак,
.
Полученная справа от вертикальной черты
квадратная матрица является обратной
к данной матрице А. Итак,
 .
.


