1.множества

Под множеством в математическом анализе понимают совокупность, собрание, набор некоторых объектов, объединяемых по какому-либо правилу (характеристическому свойству). Объекты, из которых состоят множество, называются его элементами. Множество считается заданным, если каким-либо образом указаны его элементы. Задание множества производится или перечислением его элементов, или указанием характеристического свойства. Множество обозначается заглавными буквами алфавитов, его элементы маленькими. Одно и то же множество может быть задано разными способами. В том случае, когда два множества состоят из одних и тех же элементов, говорят, что они равны или совпадают.

• Множество B содержится в множестве A (или множество B есть подмножество множества A), если каждый элемент множества B является элементом множества A. Обозначение: B ϲ A.

• Объединением множеств A и B называется множество, состоящее из всех элементов, принадлежащих хотя бы одному из этих множеств. Обозначение: A ᴗ B.

• Перечислением множеств A и B называется множество, состоящее из всех элементов, принадлежащих как множеству A, так и множеству B. Обозначение: A ᴖ B.

Вводится понятие пустого множества Ø. Следующие равенства принимаются по определению: Ø ϲ A (для любого A), A ᴖ Ø = Ø, A ᴗ Ø = A, Ø ᴖ Ø = Ø, Ø ᴗ Ø = Ø. Этими равенствами аксиоматизируется пустое множество. Пустое множество можно представить себе как множество без элементов.

• Для любого множества само это множество и пустое множество называются несобственными подмножествами. Все остальные подмножества – собственные.

• Разностью множеств A и B называется множество, состоящие из всех элементов, принадлежащих первому из них (A), но не принадлежащих второму (B). Обозначение: A \ B.

Очевидно, что A \ A = Ø (для любого A), A \ B ϲ A. Если A ϲ B, то разность B \ A называется дополнением множества A до множества B. Обозначение: A^’_B или C_B A

{a, b, c} – порядок элементов в множестве не существенен

<a, b, c> - упорядоченное множество элементов или кортеж (порядок существенен).

Два кортежа называются равными, если они одинаковой длинны и если элементы на соответствующих местах равны.

2.прямое (декартово) произведение множеств

• Прямым или декартовым произведением множеств A и B называется множество всех упорядоченных пар элементов, из которых первый элемент принадлежит первому множеству (A),а второй второму множеству (B). Обозначение A x B.

Для произвольных A и B A x B ≠ B x A. Это означает, что операция декартового умножения не подчиняется коммутативному (переместительному) закону.

Множество A x A естественно называть декартовым квадратом множества A и обозначать A².

• Прямым или декартовым произведением множеств A₁, A₂, … , A_n называется множество всех кортежей длинной n, в которых первый элемент принадлежит первому множеству (A₁), второй второму множеству (A₂), последний множеству A_n. Обозначение: A₁ x A₂ x …x A_n.

3* числовые множества

Числовые множества – это множества, элементами которых являются числа.

В основном рассматриваются числовые множества, которые носят общие наименование промежуток. Это:

• Замкнутый промежуток (отрезок) – множество вещественных чисел X, удовлетворяющих a ≤ x ≤ b, где a и b некоторые фиксированные числа, причем a<b; [a;b]. На числовой прямой отрезку соответствует геометрический отрезок с включенными в него концевыми точками.

• Открытый промежуток (интервал) – это множество вещественных чисел X, удовлетворяющих a < x < b; (a;b).

• Полуинтервал – это множество вещественных чисел X, удовлетворяющих a≤ x < b (или a < x ≤ b); [a;b), (a;b].

• Бесконечный интервал – это множество вещественных чисел X, удовлетворяющих -∞ < x < +∞; (-∞;+∞).

[a; +∞) – тоже бесконечный интервал. (a < x +∞)

<a,b> = [a;b] v (a;b) v (a;b] v [a;b) Возможно a= -∞, b= +∞

4. переменная величина. функция одной переменной. элементарные функции

Величина, принимающая различные численные значения, называется переменной величиной.

Величина, принимающая только одно численное значение, называется постоянной.

Множество всех численных значений, которые может принимать данная переменная величина, называется областью ее изменения. Задать переменную величину x значит задать область ее изменения X.

Определение. Переменная величина y называется функцией переменной величины x, если каждому числовому значению x из области ее изменения соответствует одно определенное численное значение переменной y. В этом случае пишут y=f(x). Переменная x называется аргументом; переменная y – функцией; f – характеристикой функции.

Область изменения переменной x называется область определения (или область задания) функции. Область изменения переменной y называется областью значения функции. Для характеристики функции используются различные буквы и символы.

Если функция обозначена через f(x), то через f(x₀) обозначается соответственно значение функции в точке x₀.

Для функции применяется наглядное геометрическое изображение. Графиком функции y=f(x) называется линия, для которой равенство служит уравнением.

Следует помнить, что зависимость между переменными величинами не во всех случаях имеет функциональный характер.

Определение (на языке множеств): Пусть даны два множества X и Y. Говорят, что на множестве X задана функция, принимающая значения множества Y, если по некоторым правилам или закону f каждому элементу множества X поставлен в соответствие один и только один элемент множества Y. При этом пишут f: x→y или y=f(x), x є X, y є Y.

Множество X называется областью определения функции X=D(f), множество Y называется областью значений функции Y=E(f).

Основными элементарными функция называют функции следующего вида:

• Константная y=C, x є (-∞;+∞)

• Степенная y=x^α (α=const, D(f) зависит от природы показателя)

• Показательная y=a^x (a=const>0, a≠1; D(y)=R)

• Логарифмическая y=log_a x (a=const>0, a≠0; D(y)=(0;+∞))

• Тригонометрическая y=sin x, y=cos x, y=tg x, y=ctg x, y=sec x, y=cosec x; (sec x=1/cos x, cosec x=1/sin x)

• Обратные тригонометрическим y=arcsin x, y=arccos x, y=arctg x, y=arcctg x, y=arcsec x, y=arccosec x.

С помощью сложения, вычитания, умножения и деления можно получить новые функции: f(x)±y(x), f(x)*y(x), f(x)/y(x), y(x)/f(x).

Из двух функций можно образовать новую функцию, если взять функцию от функции. Функция f(γ(x)) называется сложной (или суперпозицией f и γ), где γ внутренняя функция супер позиции, f – внешняя.

Термин «сложная» характеризует не саму функцию, а способ ее задания.

Элементарными называются функции, которые получаются из основных элементарных функций с помощью сложения, вычитания, умножения, деления, суперпозицией.

5* Примеры задания функции

Функция считается заданной, если указано правило, позволяющие для каждого значения аргумента найти соответствующие значение функции.

Пример 1. y=√x; x є [0;+∞)

Здесь символ √x означает извлечение квадратного корня.

Пример 2. y=E(x) – называется эта функция «целая часть» и задается правилом y – целая часть числа x (y – целое число, удовлетворяющие y ≤ x < y+1)

На практике для задания функций часто используют таблицы и графики.

Если задано уравнение F(x,y)=0, связывающее функцию y и аргумент x, то говорят, что функция задана неявно. Ее часто называют неявной функцией, при этом термин «неявная» характеризует не саму функцию, а способ ее задания.

Пример 1. x³+y³-1=0 – это уравнение задает функцию y(x) неявно. y=³√1-x³ – явное задание функции y.

Пример 2. Уравнение x-sin y=0 (|x|≤1) задает бесконечно много функций. Одной из этих функций является y=arcsin x. Все функции, определенные данным уравнением, могут быть заданы в виде y=(-1)^k arcsin x+πk, k є Z. Это множество функций обозначается символом y=Arcsin x

Пример 3. Уравнение x²+y²=1 задает две функции y=√1-x² и y=-√1-x²

6* Абсолютная величина, ее свойства. окрестность точки

Как известно абсолютной величиной (или модулем) называют число |x|, определенное условием

x, если x>0

|x|= -x, если x<0

0, если x=0

Если число x изобразить на числовой прямой точкой M, то |x| сопоставлен с длинной отрезка OM.

Из определения модуля вытекает, что всегда |x|≥0, |-x|=|x|, x≤|x|, -x≤|x|

Можно доказать следующие важные свойства абсолютных величин

• |x|<α равносильно –α<x<α. Замечание |x|≤α равносильно -α≤x≤α

• Если |x|>α, то x>α или x<-α. Замечание если |x|≥α, то x≥α или x≤-α

• |x+y|≤|x|+|y|

• |x-y|≥|x|-|y|

• |x*y|=|x|*|y|

• |x/y|=|x|/|y|

Окрестность числа x₀ называется всякий интервал (α;β) такой что x₀ є (α;β).

Пусть δ>0 – какое-либо положительное число. Решим относительно x неравенство |x-x₀|<δ. По свойству 1 имеем –δ<x-x₀<δ это равносильно x₀-δ<x<x₀+δ, то есть x є (x₀-δ;x₀+δ) – этот интервал называется δ-окрестностью числа x₀. Само число δ называется радиусом окрестности. Всякая окрестность (α;β) точки x₀ содержит некоторую ее δ-окрестность.

Пусть E – какое-нибудь числовое множество.

Определение 1. Точка x₀ называется внутренней точкой множества E, если она входит в множество E с некоторой своей окрестностью (хотя бы и весьма малой).

Определение 2. Точка x₀, принадлежащая или не принадлежащая множеству E, называется граничной точкой этого множества, если любая окрестность точки x₀ содержит как точки принадлежащие множеству E, так и точки ему не принадлежащие.

7. функция бесконечно малая в точке. леммы о функциях, б.м.в т.

классический математический анализ.

Функция f(x) называется бесконечно малой в точке x₀ (или при x→x₀), если величина |f(x)| не просто мала, а как угодно мала в окрестности точки x₀, то есть, как бы ни было мало Ԑ>0, оказывается, существует такая окрестность точки x₀, для всех точек которой выполняется неравенство |f(x)|<Ԑ.

Определение. Функция f(x) называется бесконечно малой в точке x₀ (или при x→x₀), если для любого числа Ԑ>0 существует такое соответствующее ему число δ>0, что для всех значений x (из области определения функции), удовлетворяющих неравенству |x-x₀|<δ выполняется неравенство |f(x)|<Ԑ

Из определения следует, что δ зависит от Ԑ, но эта зависимость не носит функционального характера.

Пусть числу Ԑ>0 соответствует δ>0, то тогда этому Ԑ соответствует и всякое число меньше δ, то есть одному числу Ԑ соответствует бесконечное множество чисел δ, а не одно как этого требует функциональная зависимость.

Из определения вытекают следующие утверждения:

• Если f(x) – бесконечно малая в точке x₀, то -f(x) и |f(x)| бесконечно малые в точке x_0.

• Если f(x) – бесконечно малая в точке x₀ и x₀ принадлежит области определения функции, то обязательно f(x₀)=0

• Константная функция f(x)≡0 – бесконечно малая в каждой точке области определения функции

• Если f(x)≡C – константная функция, причем f(x) – бесконечно малая в точке x₀, то С=0

Лемма 1. Если |f(x)|≤α(x), где α(x) – бесконечно малая в точке x₀, то функция f(x) – бесконечно малая в точке x_0.

Доказательство. Пусть Ԑ>0 – любое положительное число. Так как α(x) – бесконечно малая в точке x₀, то существует δ>0 такое, что для любого x: |x-x₀|<δ=> |α(x)|<Ԑ=>|f(x)|<Ԑ

Итак, для любого Ԑ>0 существует δ>0 для любого x: |x-x₀|<δ=>|f(x)|<Ԑ, то есть f(x) – бесконечно малая в точке x₀.

Лемма 2. Если α(x) – бесконечно малая в точке x₀, то f(x)=C* α(x) (C=const) – бесконечно малая в точке x₀.

Доказательство. Пусть Ԑ>0 – любое положительное число. Так как α(x) – бесконечно малая в точке x₀, то для Ԑ₁=Ԑ/|C| должно существовать δ>0 такое, что для любого x: |x-x₀|<δ=> |α(x)|<Ԑ₁= Ԑ/|C|=>|f(x)|=|C*α(x)|=|C|*|α(x)|<|C|*Ԑ/|C|=Ԑ

Итак, для любого Ԑ>0 существует δ>0 для любого x: |x-x₀|<δ=>|f(x)|<Ԑ, это значит, что f(x)= C* α(x) - бесконечно малая в точке x₀.

Определение. Функция f(x) называется ограниченной в области X, если в этой области выполняется неравенство |f(x)|≤M, где M – некоторое положительное число.

Лемма 3. Произведение функции бесконечно малой в точке на ограниченную функцию есть функция, бесконечно малая в точке.

Дано: α(x) – бесконечно малая в точке x₀, f(x) – ограниченная функция, хотя бы в некоторой достаточно малой окрестности точки x₀, f(x)≤M

Требуется доказать, α(x)*f(x) – бесконечно малая в точке x₀

Доказательство. Так как α(x) – бесконечно малая в точке x₀, то |α(x)| и M*|α(x)| - бесконечно малые в точке x₀ (по лемме 2). Тогда по лемме 1 на основании неравенства |f(x) * α(x)|=|f(x)|*| α(x)|≤M*|α(x)| имеем, что для любого Ԑ>0 существует δ>0 для любого x: |x-x₀|<δ=>|f(x)* α(x)|<Ԑ, то есть f(x)* α(x) – бесконечно малые в точке x₀

Следствие. Произведение двух функций, бесконечно малых в точке есть функция, бесконечно малая в точке.

Лемма 4. Сумма нескольких функций, бесконечно малых в точке x₀, есть функция, бесконечно малая в точке x₀.

Дано: α(x) и β(x) – бесконечно малые в точке x₀

Требуется доказать, что γ(x)=α(x)+β(x) - бесконечно малые в точке x₀

Доказательство. По свойству 3 абсолютной величины имеем γ(x)|=|α(x)+β(x)|≤|α(x)|+|β(x)|

Пусть Ԑ>0 – любое положительное число. Для Ԑ₁=Ԑ/2 существует δ₁>0 такое, что для любого x: |x-x₀|<δ₁=>|α(x)|<Ԑ/2.

Для Ԑ₂=Ԑ/2 существует δ₂>0 такое, что для любого x: |x-x₀|<δ₂=>|β(x)|<Ԑ/2.

Если взять δ=min(δ₁,δ₂) – (наименьшее из чисел δ₁ и δ₂), то из |x-x₀|<δ=>|α(x)|+|β(x)|<Ԑ/2+Ԑ/2=Ԑ => |γ(x)|<Ԑ

Итак, для любого Ԑ>0 существует δ>0 для любого x: |x-x₀|<δ=>|γ(x)|<Ԑ, это значит, что γ(x) - бесконечно малая в точке x₀.

Индукцией доказанное утверждение может быть распространено на случай суммы нескольких функций, бесконечно малых в точке.

8. предел функции. теоремы о пределах.

Определение. Число A называется пределом функции f(x) в точке x₀ (или при x→x₀), если разность f(x)-A – функция бесконечно малая в точке x₀, то есть для любого сколь угодно малого числа Ԑ>0 существует такое соответствующее ему число δ>0, что для всех значений x (из области определения функции), удовлетворяющих неравенству |x-x₀|<δ выполняется неравенство |f(x)-A|<Ԑ

В символической записи: A есть предел f(x) в точке x₀, если для любого Ԑ>0 существует δ>0 для любого x: |x-x₀|<δ=>|f(x)-A|<Ԑ

Запись lim x→x₀(f(x))=A

Это же определение в геометрических терминах:

A – предел f(x) при x→x₀, если каждой Ԑ-окрестности точки A соответствует такая δ-окрестность точки x₀, что для всех x є (x₀-δ; x₀+δ) => f(x) є (A-Ԑ; A+Ԑ)

Замечание 1. Если функция f(x) – бесконечно малая в точке x_0, то lim x→x₀(f(x))=0.

Действительно, f(x)-0=f(x) – бесконечно малая в точке x₀. И наоборот, если lim x→x₀(f(x))=0, то f(x)=f(x)-0 - бесконечно малая в точке x₀.

Это можно записать так: lim x→x₀(f(x))=0 <=> f(x) бесконечно малая в точке x₀.

Замечание 2. Очевидно, что lim x→x₀(С)=С, то есть предел постоянной есть сама эта постоянная.

Теорема 1. Функция f(x) не может иметь в точке x₀, более одного предела.

Дано: lim x→x₀(f(x))=A (1), lim x→x₀(f(x))=B (2)

Требуется доказать, что A=B

Доказательство. Из равенства (1) следует, что f(x)-A=α(x) - бесконечно малая в точке x₀. Из равенства (2) следует, что f(x)-B=β(x) - бесконечно малая в точке x₀. Тогда константная функция B-A=α(x)-β(x) - бесконечно малая в точке x₀. Следовательно, B-A=0 => A=B.

Теорема 2. Предел суммы нескольких функций, имеющих предел, существует и равен сумме пределов слагаемых.

Дано: lim x→x₀(f(x))=A (3), : lim x→x₀(g(x))=B (4)

Требуется доказать, что существует предел lim x→x₀[f(x)+g(x)], причем lim x→x₀[f(x)+g(x)]= lim x→x₀(f(x))+ lim x→x₀(g(x))

Доказательство. Из равенства (3) следует, что f(x)-A=α(x) - бесконечно малая в точке x₀. Из равенства (4) следует, что g(x)-B=β(x) - бесконечно малая в точке x₀. Тогда [f(x)+g(x)]-(A+B)= α(x)+β(x) - бесконечно малая в точке x₀. По определению предела число A+B есть предел f(x)+g(x): lim x→x₀[f(x)+g(x)]=A+B (5)

Подставим A и B из равенств (3) и (4) в равенство (5), получим lim x→x₀[f(x)+g(x)]=lim x→x₀(f(x))+ lim x→x₀(g(x))

Доказанное утверждение может быть распространенно на случай суммы нескольких функций.

Теорема 3. Предел произведения нескольких функций, имеющих предел, существует и равен произведению пределов множителей.

Дано: lim x→x₀(f(x))=A (6), : lim x→x₀(g(x))=B (7)

Требуется доказать, существует предел lim x→x₀[f(x)*g(x)], причем lim x→x₀[f(x)*g(x)]= lim x→x₀(f(x))*lim x→x₀(g(x))

Доказательство. Из равенства (6) следует, что f(x)-A=α(x) - бесконечно малая в точке x₀. Из равенства (7) следует, что g(x)-B=β(x) - бесконечно малая в точке x₀. Тогда [f(x)*g(x)]=[(A+α(x))*(B+β(x))]=AB+Aβ(x)+Bα(x)+α(x)β(x). И lim x→x₀[f(x)*g(x)]= lim x→x₀(AB)+ lim x→x₀(Aβ(x) (б.м.)+ lim x→x₀(Bα(x)) (б.м.) +

+ lim x→x₀(α(x)β(x))=AB+0+0+0=AB (по теореме 2)

Таким образом, lim x→x₀[f(x)*g(x)]=AB (8). Подставим A и B из равенств (6) и (7) в равенство (8), получим lim x→x₀[f(x)*g(x)]= lim x→x₀(f(x))* lim x→x₀(g(x))

Следствие. Постоянный множитель можно выносить за знак предела, то есть lim x→x₀(C*f(x))=C*lim x→x₀(f(x)).

Доказательство. lim x→x₀(С*f(x))= lim x→x₀(С)*lim x→x₀(f(x))=С* lim x→x₀(f(x))

Теорема 4. Предел частного двух функций, имеющих предел, существует и равен частному пределов этих функций, если только предел знаменателя отличен от нуля.

lim x→x₀[f(x)/g(x)]= lim x→x₀(f(x))/ lim x→x₀(g(x)), если lim x→x₀(g(x))≠0

9. переход к пределу в неравенстве (лемма и две теоремы)

Лемма (о сохранении знака)

Если lim x→x₀(f(x))=A>0, то в некоторой окрестности точки x₀ выполняется неравенство f(x)>0.

Доказательство. Возьмем Ԑ=A/2. По определению предела существует такое δ>0, что для любого x: |x-x₀|<δ => |f(x)-A|<Ԑ, то есть –A/2<f(x)-A<A/2, -A/2<f(x)-A, -A/2+A<f(x), 0<A/2<f(x), 0<f(x)

Следствие. Если lim x→x₀(f(x))=A<0, то f(x)<0 в некоторой окрестности точки x₀.

Действительно, если lim x→x₀(f(x))<0, то lim x→x₀[-f(x)]>0, тогда в некоторой окрестности точки x₀ (по доказанному) выполняется неравенство –f(x)>0, что равносильно f(x)<0.

Теорема 1. Если lim x→x₀(f(x))<lim x→x₀(g(x)) (1), то в некоторой окрестности точки x₀ выполняется неравенство f(x)<g(x)

Доказательство. Из неравенства (1) имеем lim x→x₀[g(x)-f(x)]= lim x→x₀(g(x)) - lim x→x₀(f(x))>0

По лемме о сохранении знака в некоторой окрестности точки x₀ выполняется неравенство g(x)-f(x)>0, что равносильно неравенству f(x)<g(x)

Теорема 2. Если в некоторой окрестности точки x₀ выполняется неравенство f(x)≤g(x) (2) и пределы lim x→x₀(f(x)) и lim x→x₀(g(x)) существуют, то lim x→x₀(f(x))≤lim x→x₀(g(x)) (3), то есть в неравенстве можно переходить к пределу.

Доказательство. Допустим противное. Пусть неравенство (3) не имеет места, то есть lim x→x₀(f(x))> lim x→x₀(g(x)). Но тогда по теореме 1. в некоторой окрестности точки x₀ справедливо неравенство f(x)>g(x), что противоречит условию (2)

10. теорема о сжатой переменной

еорема. Если g(x)≤f(x)≤h(x) (1) и lim x→x₀(g(x))=A= lim x→x₀(h(x)) (2), то предел lim x→x₀(f(x)) существует, причем lim x→x₀(f(x))=A.

Доказательство. Из равенства (2) следует, что g(x)-A=α(x) - бесконечно малая в точке x₀. h(x)-A=β(x) - бесконечно малая в точке x₀ (‘это равенства 3). Из неравенства (1) получаем g(x)-A≤f(x)-A≤h(x)-A. Отсюда, используя равенства (3) и свойства абсолютной величины имеем.

-|α(x)|-|β(x)|≤-|α(x)|≤α(x)≤f(x)-A≤β(x)≤|β(x)|≤|β(x)|+|α(x)|.

Следовательно |α(x)|+|β(x)|≤f(x)-A≤|β(x)|+|α(x)|, то есть |f(x)-A|≤|α(x)|+|β(x)| (4)

Так как правая часть неравенства (4) есть функция, бесконечно малая в точке x₀ (по лемме 4 о бесконечно малых), то из этого неравенства по лемме 1 о бесконечно малых следует, что f(x)-A - бесконечно малая в точке x₀, то есть A=lim x→x₀(f(x)).

11. предел отношения синуса к бесконечно малому аргументу

Рассмотрим тригонометрический круг радиуса R. Пусть φ обозначает радиальную меру некоторого положительного или отрицательного угла AOM. Согласно определению синуса и косинуса имеем sin φ=BM/R, cos φ=OB/R

Отсюда следует, что lim φ→0(sin(φ))=0, lim φ→0(cos(φ))=1.

Нашей задачей является доказать, что lim φ→0(sin(φ)/φ) – существует,

причем lim φ→0(sin(φ)/φ)=1

Доказательство. Для 0<φ<π/2 имеем S_{тр, AOM}<S_{серт. AOM}<S_{тр. OAC};

1/2R²sin φ<1/2R²φ<1/2R²tg φ

sin φ<φ<tg φ 1<φ/sin φ<1/cos φ, cos φ<sin φ/φ<1

Следовательно, при 0<φ<π/2, cos φ<sin φ/φ<1 (1)

Пусть теперь –π/2<φ<0.

Так как 0<-φ<π/2, то из неравенства (1) получаем cos (-φ)<sin (-φ)/(-φ)<1.

И при –π/2<φ<0 получаем такое же неравенство cos φ<sin φ/φ<1.

Итак, cos φ<sin φ/φ<1, -π/2<φ<π/2, φ≠0 (2).

Так как lim φ→0(cos(φ))=1= lim φ→0(1), то из неравенства (2) по теореме о сжатой переменной следует, lim φ→0(sin(φ)/φ)=1

12. функции, бесконечно большие в точке

Определение. Функция f(x) называется бесконечно большой в точке x₀ (или при x→x₀), если f(x) не обращается в нуль в некоторой окрестности точки x₀, и обратная величина 1/f(x) – функция, бесконечно малая в точке x₀.

Обозначение: lim x→x₀(f(x))=∞

Принято говорить, что f(x) имеет бесконечный предел, хотя при x→x₀ функция f(x) предела не имеет.

Замечание. Если в записи lim x→x₀(f(x))=A, A – число, то чтобы подчеркнуть это обстоятельство, иногда говорят, что функция f(x) имеет в точке x₀ конечный предел.

Если lim x→x₀(f(x))=∞ и f(x)>0 в некоторой окрестности точки x₀, то пишут lim x→x₀(f(x))=+∞. Если lim x→x₀(f(x))=∞ и f(x)<0 в некоторой окрестности точки x₀, то пишут lim x→x₀(f(x))=-∞.

Символ lim x→∞(f(x)) применяют для обозначения предела lim t→0 (f(1/t)). Следовательно, lim x→∞(f(x)) по определению равен lim t→0 (f(1/t)).

Для обозначения lim x→∞_x>0(f(x)) применяют обозначение lim x→+∞ (f(x)) или еще более краткое f(+∞). Аналогично f(-∞)=lim x→-∞ (f(x))= lim x→∞_x<0(f(x)).

13. предел числовой последовательности

Функцию натурального аргумента f(n), где n=1,2,.., называют числовой последовательностью. Область определения функции есть множество всех натуральных чисел N.

Натуральный аргумент часто указывают в виде индекса, а саму числовую последовательность записывают, например, так: {u_n}^∞_n=1, где u_n – общий (или n-ый) член последовательности.

Определение предела числовой последовательности можно получить из общего определения предела функции, а именно lim n→∞(f(n))=A означает, что предел lim 1/n→0(f(n))=A, то есть для любого числа Ԑ>0 существует такое число δ>0, что для всех значений n (удовлетворяющих неравенству |1/n-0|<δ) выполняется неравенство |f(n)-A|=Ԑ

Неравенство |1/n-0|<δ можно записать в виде 1/n<δ или n>1/δ, а если вместо δ ввести число N=1/δ, то в виде – n>N.

Итак, lim n→∞(f(n))=A, если для любого Ԑ>0 существует N для любого n: n>N => |f(n)-A|<Ԑ.

14. точная верхняя граница

Рассмотрим некоторое множество чисел E. Это множество изображается множеством точек на числовой прямой.

Число M называется верхней границей множества чисел E, если x≤M для всех xєE

Очевидно, верхняя граница изображается точкой, лежащей правее всех точек множества E. Аналогично определяется нижняя граница множества чисел.

Множество, имеющее верхнюю границу, называется ограниченной сверху.

Множество, имеющее нижнюю границу, называется ограниченной снизу.

Верхняя граница множества значений функции, называется верхней границей этой функции. Аналогично, нижняя граница функции.

Определение 1. Наименьшая верхняя граница множества E называется точной границей (или супремумом) множества E и обозначается sup E.

Определение 2. Наибольшая нижняя граница множества E называется точной нижней границей (или инфимумом) множества E и обозначается inf E.

Отметим следующее. Бесконечное множество чисел может не содержать наименьшего или наибольшего числа.

Вопрос: всякое ли множество имеет такую верхнюю границу. Конечно же, нет. Если множество не ограничено сверху, то есть не имеет ни одной верхней границы, то оно не имеет и точек верхней границы.

Поставим вопрос несколько иначе. Если множество ограниченно сверху, то есть имеет верхние границы, то обязательно ли среди бесконечного множества верхних границ имеется наименьшая верхняя граница. (Да)

Теорема. Всякое непустое ограниченное сверху множество имеет точную верхнюю границу (без доказательства).

15. предел монотонной функции

Теорема. Если функция натурального аргумента (числовой последовательности) f(n) не убывающая и ограниченная сверху, то lim n→∞(f(n)) существует.

Доказательство. Согласно предыдущей теореме f(n) имеет точную верхнюю границу M=sup f(n): f(n)≤M для любого n.

Докажем, что lim n→∞(f(n))=M

Пусть Ԑ>0 – любое положительное число. Число M-Ԑ - не является верхней границей функции f(n), так как M – точная верхняя граница.

Следовательно, существует такое значение f(N), которое будет больше M-Ԑ: f(N)>M-Ԑ (1)

Так, как f(n) неубывающая функция, то для любого n: n>N => f(n)>f(N) (2)

Из неравенства (1) и (2) следует, что для любого n: n>N => f(n)>M-Ԑ,

M-Ԑ<f(n)≤M<M+Ԑ

-Ԑ<f(n)-M<Ԑ, то есть |f(n)-M|<Ԑ

Итак, для любого Ԑ>0 существует N>0 для любого n: n>N => |f(n)-M|<Ԑ. Следовательно, lim n→∞(f(n))=M.

Замечание 1. Если f(n) – неубывающая функция, не ограниченна сверху, то lim n→∞(f(n))=+∞

Замечание 2. Аналогичная теорема имеет место для невозрастающей, ограниченной снизу функции.

16. специальные пределы

1. Первый замечательный предел.

lim x→0(sin (x)/x)=1 (1) – получено ранее.

2. Второй замечательный предел

Рассмотрим функцию натурального аргумента f(n)=(1+1/n)ⁿ

Вычислим f(1)=2¹=2, f(2)=(3/2)²=2,25, f(3)=(4/3)³=64/27≈2,37 и так далее.

В теории пределов доказывается, что lim n→∞((1+1/n)ⁿ) существует, причем lim n→∞((1+1/n)ⁿ)=e (2), где e≈2,718281... – иррациональное число. e – неперово число.

Наряду с формулой (2) имеет место и более общая формула

lim x→∞((1+1/x)^x)=e (3)

В частности, lim x→+∞((1+1/x)^x)=e (3а), lim x→-∞((1+1/x)^x)=e (3б)

Кроме того, по определению имеем e= lim x→∞((1+1/x)^x)= lim t→0((1+t)^1/t)

Таким образом, lim x→0((1+x)^1/x)=e (4) - 1^∞ - неопределенность.

Логарифмы по основанию e называются натуральными и обозначаются ln. Функция y=ln x является обратной для показательной функции y=e^x.

3. Рассмотрим lim x→0((log_a (1+x))/x)=(0/0)= lim x→0(log_a (1+x)^1/x)= =log_a lim x→0((1+x)^1/x)=log_a e=1/ln a (a=const>0, a≠1)

Таким образом, lim x→0((log_a (1+x))/x)=1/ln a (5)

Замечание 1. Если в формуле (5) положить a=e, то получим более простую формулу (сказывается особая роль природы числа e) lim x→0((ln (1+x))/x)=1 (6).

4. Вычислим lim x→0((a^x-x))/x) (a-const>0, a≠1)

Полагаем, a^x-1=t. Тогда a^x=1+t x*ln a=ln (1+t), x=(ln (1+t))/ln a

Очевидно, t→0 при x→0. Поэтому lim x→0((a^x-x))/x)= lim t→0(t/((ln (1+t))/ln a))= =lim t→0(ln a/((ln (1+t))/t))=ln a ((ln (1+t))/t≈1)

Таким образом, lim x→0((a^x-x))/x)=ln a (7)

Замечание. Если a=e, то получаем более простую формулу lim x→0((a^x-x))/x)=1 (8)

5. Вычислим lim x→0(((1+x)^α-1)/x) (α-const≠0)

Обозначим 1+x=e^t. Тогда (1+x)^α-1=e^αt-1; x=e^t-1

Очевидно, t→0 при x→0. Поэтому lim x→0(((1+x)^α-1)/x)= lim t→0((e^αt-1)/(e^t-1))= =lim t→0(((e^αt-1)/αt)*(t/(e^t-1))*α)= lim t→0((e^αt-1)/αt)* lim t→0(t/(e^t-1))*α=α

(lim t→0((e^αt-1)/αt)=1, lim t→0(t/(e^t-1))=1)

Итак, lim x→0(((1+x)^α-1)/x)=α (9)

17. сравнение функций, бесконечно малых в точке

Когда сравнивают два числа a и b, то рассматривают их отношение b/a (или a/b).

Аналогично поступают с двумя бесконечно малыми в точке x₀ функциями α(x) и β(x), только берут не просто их отношение, а предел их отношения lim x→x₀(β(x)/α(x)).

Рассмотрим три случая:

1. lim x→x₀(β(x)/α(x))=С≠0. В этом случае бесконечно малые α(x) и β(x) называются бесконечно малыми одного порядка малости. В частности, если lim x→x₀(β(x)/α(x))=1, то бесконечно малые α(x) и β(x) называются эквивалентными. Это обозначается так β(x)͠ α(x)

2. lim x→x₀(β(x)/α(x))>0, то есть lim x→x₀(α(x)/β(x))=∞. Бесконечно малая β(x) называется бесконечно малой высшего порядка малости по сравнению с бесконечно малой α(x). Это записывается так: β(x)=0(α(x)). (Читается «0» маленькое от альфа от икс)

3. lim x→x₀(β(x)/α(x)) не существует. В этом случае бесконечно малые α(x) и β(x) называются несравнимыми.

Теорема 1. Предел отношения двух функций, бесконечно малых в точке, не изменится, если каждую из них заменить эквивалентной ей бесконечно малой функцией.

Дано: при x→x₀ α(x)͠ α₁(x), β(x)͠ β₁(x)

Доказать lim x→x₀(β₁(x)/α₁(x))= lim x→x₀(β(x)/α(x))

Доказательство. β(x)/α(x)=β(x)/β₁(x)*β₁(x)/α₁(x)*α₁(x)/α(x)

Отсюда lim x→x₀(β(x)/α(x))= lim x→x₀(β(x)/β₁(x))* lim x→x₀(β₁(x)/α₁(x))* *lim x→x₀(α₁(x)/α(x))= lim x→x₀(β₁(x)/α₁(x))

(lim x→x₀(β(x)/β₁(x))=1, lim x→x₀(α₁(x)/α(x))=1)

Теорема 2. Если функция β(x) – бесконечно малая высшего порядка малости по сравнению с бесконечно малой α(x), то α(x)+β(x)͠ α(x).

Иначе говоря: если в сумме отбросить бесконечно малое слагаемое по сравнению с другим слагаемым, то получим бесконечно малую, эквивалентную сумме.

Доказательство. lim x→x₀((β(x)+α(x))/α(x))= lim x→x₀(α(x)/α(x))+ +lim x→x₀(β(x)/α(x))=1+0=1, то есть α(x)+β(x)͠ α(x). (lim x→x₀(β(x)/α(x))=0)

Когда сравнивают несколько постоянных величин, то поступают следующим образом: одну из них выбирают за единицу и этой единицей измеряют все оставшиеся величины. Аналогично поступают с бесконечно малыми функциями. Одну из них выбирают за основную бесконечно малую, и все остальные сравнивают с этой основной.

Пусть бесконечно малая α(x) выбрана за основную бесконечно малую. Тогда бесконечно малая вида Cα^k(x); C-const≠0, называется простейшей бесконечно малой k-того порядка. Главной часть бесконечно малой β(x) называется простейшая бесконечно малая Cα^k(x), эквивалентная ей: β(x)͠ Cα^k(x).

Порядком бесконечно малой называется порядок ее главной части. Таким образом, порядок β(x) равен порядку Cα^k(x), то есть равен k.

Пусть α(x) – основная бесконечно малая. Если β(x)= Cα(x)+0(α(x)) (1), то бесконечно малая Cα(x) называется линейной частью бесконечно малой β(x).

Очевидно, что lim x→x₀(β(x)/α(x))=C (2).

И обратно, из равенства (2) следует равенство (1).

Таким образом, если бесконечно малая β(x) – 1-го порядка, то линейная часть β(x) равна главной части β(x), если β(x) – порядка выше первого, линейная часть β(x) равна нулю.

Замечание. Аналогично сравниваются функции бесконечно большие в точке.

18* односторонние пределы

Для изучения поведения функции f(x) вблизи точки x₀ важное значение имеет lim x→x₀(f(x)). Если lim x→x₀(f(x)) – не существует, то рассмотрим пределы с дополнительными ограничениями: f(x₀-0)= lim x→x₀-0(f(x))=lim x→x0_x<x0(f(x)) (1)

f(x₀+0)=lim x→x₀+0(f(x))=lim x→x0_x>x0(f(x)) (2)

Пределы (1) и (2) называются односторонними пределами функции f(x) в точке x₀. При этом f(x₀-0) называется пределом функции слева, а f(x₀+0) – пределом функции справа.

Очевидно, что если lim x→x₀(f(x)) – существует, то существуют и оба односторонних предела, причем f(x₀-0)=f(x₀+0)=lim x→x₀(f(x)) (3)

Геометрический смысл односторонних пределов.

Рассмотрим функцию y=f(x), график которой имеет следующий вид.

Имеем f(x)=M₁M

f(x₀-0)= f(x₀-0)= lim x→x₀-0(f(x))=lim x→x₀-0(M₁M)=M₀A;

f(x₀+0)= f(x₀-0)= lim x→x₀+0(f(x))=lim x→x₀₊0(M₁M)=M₀B

19. непрерывность функции. точки разрыва и их классификация

Термин «непрерывность функции» связан с интуитивным представлением о непрерывности линии, являющейся графиком функции.

Пусть функция y=f(x) имеет в точке x₀ непрерывный график.

Тогда: lim x→x₀(MM^’)= lim x→x₀(M₀M₀^’)

MM^’=f(x); M₀M₀^’=f(x₀); lim x→x₀(f(x))=f(x₀)

Последнее равенство и приняли за определение непрерывности функции.

Определение. Функция f(x) называется непрерывной в точке x₀, если lim x→x₀(f(x))=f(x₀) (1)

Равенство один можно переписать так: lim x→x₀(f(x))=f(lim x→x₀(x)), то есть для непрерывности функции можно переходить к пределу под знаком функции.

Или иначе: для неопределенности функции знак предела и характеристику функции можно менять местами.

Легко видеть, что равенство (1) эквивалентно равенствам: f(x₀-0)=f(x₀)=f(x₀+0) (2)

если lim x→x₀(f(x)) не существует, то (независимо от того, определена функция f(x) в точке x₀ или нет) говорят, что f(x) терпит в точке x₀ разрыв.

Разрывы функции делятся на разрывы 1-го и 2-го рода. Разрыв функции f(x) в точке x₀ называется разрывом функции 1-го рода, если существуют оба односторонних предела f(x₀-0) и f(x₀+0).

Разрыв функции f(x) в точке x₀ называется разрывом 2-го рода, если не существует хотя бы один из односторонних пределов f(x₀-0) или f(x₀+0).

Чаще всего разрыв 2-го рода – это так называемый бесконечный разрыв, когда функция в точке разрыва обращается в ∞. Однако следует иметь в виду, что разрывы 2-го рода имеют место, когда функция не обращается в ∞.

На практике чаще приходиться иметь дело с бесконечными разрывами 2-го рода.

Процессы, с которыми приходится встречаться в природе, чаще всего описывается непрерывными функциями. Однако встречаются процессы с количественными скачками. Количественные скачки всегда сопровождаются качественными изменениями. В виде примера рассмотрим процесс нагревания вещества. Обозначим Q – количество тепла, сообщенное веществу, t – температура вещества. В точке t₀ плавления и t₀ кипения функция имеет разрывы.

20. операции над непрерывными функциями

Теорема 1. Если функция f(x) и g(x) непрерывны в точке x₀, то их сумма, разность, произведение, частное являются непрерывными функциями в точке x₀.

Докажем теорему для частного. Дано: lim x→x₀(f(x))=f(x₀); lim x→x₀(g(x))=g(x₀)≠0

Требуется доказать функция F(x)=f(x)/g(x) непрерывна в точке x₀, то есть lim x→x₀(F(x))=F(x₀).

Доказательство

lim x→x₀(F(x))= lim x→x₀(f(x)/g(x))= lim x→x₀(f(x))/lim x→x₀(g(x))=f(x₀)/g(x₀)=F(x₀).

Теорема 2. Если y=f(u) – непрерывная функция от «u», а u=u(x) – непрерывная функция от x, то их суперпозиция y=f(u(x)) – непрерывная функция от x.

Коротко: непрерывная функция от непрерывной функции непрерывна.

Доказательство. lim x→x₀(f(u(x)))=f(lim x→x₀(u(x)), так как f – непрерывная функция.

lim x→x₀(u(x))= u(lim x→x₀(x), так как u – непрерывная функция.

Следовательно, lim x→x₀(f(u(x)))=f(u lim x→x₀(x)), то есть f(u(x)) – непрерывная функция от x в точке x₀.

Теорема 3. Если y=f(x) – непрерывна, строго монотонная на [a;b],то обратная для нее функция x=φ(y) так же непрерывна (без доказательства)

Функцию f(x) непрерывную в каждой точке некоторого промежутка, называют непрерывной на этом промежутке.

21. теоремы Больцано-Коши (кого????????????????????). теорема Вейерштрасса (чееееееееее????)

Теорема (1-я теорема Больцано-Коши). Если функция f(x) – непрерывна на отрезке [a;b] и принимает на концах этого отрезка значение разных знаков, то на этом отрезке существует, по меньшей мере, 1 точка C, в которой f(C)=0 (без доказательства)

Теорема совершенно очевидна из геометрического представления функции.

Теорема (2-я теорема Больцано-Коши). Функция f(x), непрерывна на отрезке [a;b], принимает на концах отрезка соответствующие значения A, B, принимает на этом отрезке и все промежуточные значения между A и B.

Доказательство. Пусть для определенности A<B и пусть A<C<B.

Докажем, что существует точка C такая, что f(C)=C, где С є (a;b).

Рассмотрим функцию F(x)=f(x)-C. Тогда имеем F(a)=f(a)-C=A-C<0

F(b)=f(b)-C=B-C>0

По 1-й теореме Больцано-Коши найдется точка C, принадлежит (a;b) такая, что F(C)=0, то есть f(C)-C=0 или f(C)=C.

Замечание. Эту теорему часто формулируют так: непрерывная (на некотором промежутке) функция, приняв два значения, принимает и все промежуточные.

Теорема Вейерштрасса. Функция f(x), непрерывная на [a;b], ограниченна на этом промежутке и принимает на нем как свое наименьшее, так и свое наибольшее значение (без доказательства).

Замечание. Требование непрерывности на отрезке, то есть на замкнутом промежутке, здесь также существенно, как в теоремах Больцано-Коши.

22. приращение аргумента и функции. определение непрерывности функции на языке приращений.

Рассмотрим функцию y=f(x).

Пусть точка x – близкая к точке x₀.

Введем обозначение ∆x=x-x₀, ∆y=f(x)-f(x₀) (1).

При этом ∆x называется приращением аргумента, ∆y – называется приращением функции. На знак ∆x ограничений не налагаем (лишь бы точки x и x₀ принадлежали ООФ). Символы ∆x и ∆y следует рассматривать как цельные, неразлучные символы (∆ не есть множитель, а заменяет слово «приращение»)

Из равенства (1) => x=x₀+∆x – приращение значения аргумента.

f(x)=f(x₀+∆x) – приращение значения функции.

∆y=f(x₀+∆x)- f(x₀) – приращение функции y=f(x) в точке x₀.

Вместо ∆y часто пишут ∆f(x₀).

Геометрический смысл величин ∆x, ∆y (∆f(x₀)) можно показать на рисунке.

Важно заметить, что приращение функции ∆ f(x₀) зависит, во-первых, от точки x₀, во-вторых, от того приращения ∆x аргумента, которое вызвало это приращение.

В терминах приращение можно иначе сформулировать определение непрерывности функции. Запишем равенство, служащие определением непрерывности функции f(x) и точке x_0.

lim x→x₀(f(x))=f(x₀) (2)

Положим x-x₀=∆x. Тогда x=x₀+∆x, ∆x→0 при x→x₀ и равенство (2) перепишется в виде lim ∆x→0(f(x₀+∆x))=f(x₀) или lim ∆x→0[f(x₀+∆x)-f(x₀)]=0, то есть в наших обозначениях lim ∆x→0(∆f(x₀))=0 (3).

Равенства (2) и (3) равносильны, поэтому равенство (3) является новым, вторым, определением непрерывности функции f(x) в точке x₀.

Определение (3) можно выразить в такой форме: функция непрерывна, если бесконечно малое приращение аргумента вызывает бесконечно малое приращение функции.

23. непрерывность элементарных функций

Можно показать, что все основные элементарные функции непрерывны в ООФ. В виде примера докажем непрерывность функции y=sin x.

Эта функция определена на всей оси Ox. x є (-∞;+∞)

Для любого x є (-∞;+∞) ∆sin x=sin (x+∆x)-sin x=2sin ∆x/2*cos (x+∆x/2)

Так как sin ∆x/2 – бесконечно малая при ∆x→0, а величина 2cos (x+∆x/2) – ограничена, то имеем произведение функции, бесконечно малой на ограниченную. Это есть функция бесконечно малая (по лемме 3 о бесконечно малых), то есть lim ∆x→0(∆sin x)=0, что и требовалось доказать.

Из непрерывности всех основных элементарных функций и из теории о непрерывности суммы, произведения, частного и суперпозиции непрерывных функций следует непрерывность всех элементарных функций в ООФ.

Дифференциальное исчисление функций одной переменной 1. задачи, приводящие к понятию производной. Производная функция в точке, ее физический смысл

Пусть по прямой, по некоторому закону движется математическая точка M. Расстояние до точки M от начала отсчета 0 обозначим через S. Найти скорость в момент t точки M свободно падающей в пустоте.

Известно, что в этом случае закон движения задается формулой: 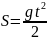. Тогда

или

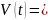
Рассмотрим тонкий стержень, на котором неравномерно распределена масса. Метод абстракции приводит к понятию материального отрезка, т.е. отрезка прямой, на котором распределена масса. Пусть m(x)- масса отрезка [a,x]. Дадим определение линейной плотности точки х. для этого рассмотрим отрезок 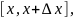его масса 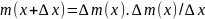– средняя линейная плотность на отрезке 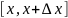, а –линейная плотность в точке х.

0	a	x	x+Δx	b

Если существует конечный или бесконечный предел 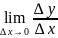, то этот предел называется производной от функции по переменной х в точке х₀. Скорость точки М в момент времени t равна производной расстояния по времени - механический смысл производной.

Определение. Предел отношения приращения функции к вызвавшему его приращению , когда 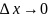, называется производной этой функции. Процесс нахождения производной функции называется дифференцированием.

2. производные некоторых элементарных функций (y=sin x, y=cos x и т.д.)

Производная синуса. Для любого

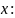
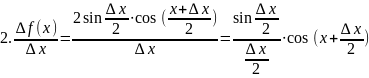
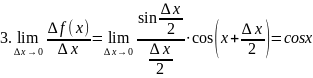
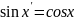(1)

производная косинуса. Для любого

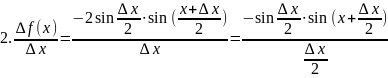
(2)

Производная показательной функции.

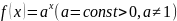
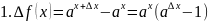
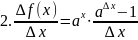
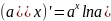(3)

Производная логарифмической функции.

(4)

3. Геометрический смысл производной. Касательная и нормаль к плоской линии, их уравнения

Рассмотрим в плоскости oxy непрерывную линию . Возьмем на этой линии 2 точки – M с абсциссой X и точку M’ с абсциссой

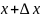
Проведем через M и M’ секущую

Определение. Прямая MT называется касательной к линии в точке M, если угол между секущей и этой прямой стремится к 0, когда расстояние между точкой M и M’ стремится к нулю, по какому бы закону точка M’ перемещаясь по линии, не приближалась к MT.

Замечание. Не следует думать, что любая линия в каждой точке обязательно обладает касательной.

Пусть K₁ – угловой коэффициент секущей, K – угловой коэффициент касательной MT

Из определения касательной:

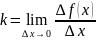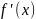, то , т.е. производная равна уголовому коэффициэнту касательной, проведенной к графику функции в точку с абсциссой

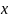
Рассмотрим в плоскости oxy линию, заданную уравнением 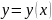и на ней точку

Уравнение касательной к линии в точке 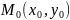запишем как уравнение прямой, проходящей через точку и имеющей угловой коэффициент 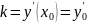получим (1)

Примечание. проходящее через точку , перпендикулярно касательной называется нормалью к линии в точке

Тогда уравнение нормали можно записать в виде:

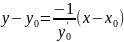(2)

4. дифференцируемость функции. теорема о непрерывности дифференцируемой функции Определение. Если производная 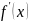существует, то функция называется дифференцируемой

Теорема. Из дифференциальности следует непрерывность

Действительно,

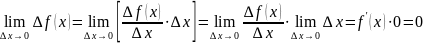
Замечание. Обратное уравнение неверно. Из непрерывности функции не следует ее дифференцировать. Например, функция 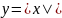непрерывна в точке 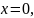но не имеет производной в этой точке

5* производная суммы, произведения, частного

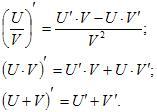
Тема. Производная суммы.

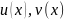Рассмотрим функцию , функции дифференцируемы. Тогда тоже дифференцируема и

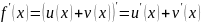
Действительно,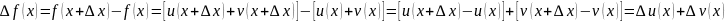

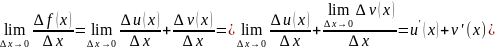т.е.

(1)

Тема. Производная произведения

Рассмотрим функцию 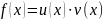, функции дифференцируемы. Тогда тоже дифференцируема и

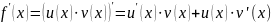
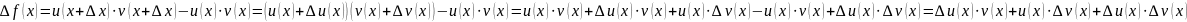
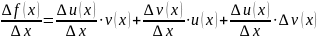
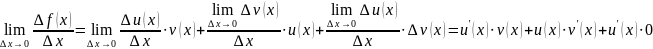
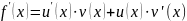(2)

6. производная обратной функции. производные функций y=arctg x, y=arcctg x, y=arcsin x, y=arccos x

Пусть f(x)-диф-ма, f’(x)≠0, ∆х и ∆у-соответствующие приращения переменных х и у.

∆х/∆y=1/∆у/∆х. перейдем в равенстве к пределу при ∆х 0.т.к функция f(x)-диф-ма, а значит и непрерывна, тo lim ∆y=0 (∆x 0).

Имеем Lim ∆x/∆y =lim 1/∆y/∆x (∆y 0) т.е. x’y=1/y’x.

Если функция имеет нулевую или бесконечную производную. То обратная ф-я в соответствующей точке имеет бесконечную или нулевую производную.

y=arctg x. x=tg y, x’y = (tg y)’y=1/cos²y=1+tg²y=1+x²

y’_x=1/x’_y=1/1+x² аналогично y=arcctg x

y=arcsin x. -1<x<1, x=sin y, -∏/2<y<∏/2; x’_y=(sin)’_y= cos y=+√1-sin²y = √1-x² ;

y’_x=1/x’_y=1/√1-x² аналогично y=arccos x.

7. производная сложной функции

y=f(g(x)). y=f(u), u=g(x).

Если y=f(u)-диф-ма от “u”, а u=g(x)-диф-ма от х, то и сложная ф-я y=f(g(x)) будет диф-мой от х, причем y’_x=y’_u*y’_x

Пусть приращение аргумента ∆х вызывает приращение постоянного аргумента ∆U. Приращение промежуточного аргумента ∆u вызывает приращение ф-ии ∆у. следовательно, приращения аргумента ∆х вызывает приращение ф-ии ∆у. ∆у/∆x=(∆y/∆u)*(∆u/∆y)

Перейдем к пределу при ∆х 0. Т.к. ф-я u=g(x)-диф-ма, а следовательно, и непрерывна, то ∆u 0 при ∆х 0.

Lim ∆y=lim ∆y/∆u*lim ∆u/∆x (∆u 0).

y’_x=y’_u*u’_x

8. параметрический способ задания функциональной зависимости. дифференцирование функций, заданных параметрически.

На примере объема и площади шара. Каждому значению переменно S соответствует одно определенное значение переменно V. S=4Пr², v=4/3Пr³. Данная система определяет функциональную зависимость между переменными s,v

Теперь исключим переменную r. S³/v³=(4³п³*r⁶)/(4²/3²*П²r⁶)=36П. s³-36Пv³=0.

Пусть функц зависимость у от х задана параметрически системой: x=x(t) y=y(t).

Y’_x=dy/dx=dy/dt/dx/dt=y’_t/x’_t.

9. дифференциал функции. геометрический смысл дифференциала

Дифференциалом ф-и называют произведение производной ф-и по независимой перемнной на произвольное преращение это переменной. Замена преращений ф-и ее диф-лом означает переход от данной ф-ой зависимости к линейной ф-и.

10* дифференциал независимой переменной

 Под дифференциалом dx независимой x понимают любое, не зависящее от x число, поэтому, по определению, дифференциалом независимой переменной x называют ее приращение  x, т.е. полагают, что dx= x. Введенное определение оправдывается следующими рассуждениями. Рассмотрим независимую переменную x как функцию вида y=x, тогда  .

Таким образом, если аргумент x функции y=f(x) является независимой переменной, то  Замечание.   - есть число, а   - отношение неопределенных чисел dy и dx, которые изменяются пропорционально коэффициентом пропорциональности  .

11* Дифференциал суммы, произведения, частного

2.3. Дифференциал суммы, произведения, частного

Теорема 13. Пусть функции u = u(x), v = v(x) дифференцируемы.

Тогда

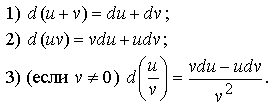
Доказательство

Теорема доказана.

12. дифференциал сложной функции (инвариантность формы дифференциала)

Цепное правило (правило дифференцирования сложной функции) позволяет вычислить производную композиции двух и более функций на основе индивидуальных производных. Если функция f имеет производную в точке x₀, а функция g имеет производную в точке y₀ = f(x₀), то сложная функция h(x) = g(f(x)) также имеет производную в точке x₀. Пусть даны функции, определённые в окрестностях на числовой прямой,   где y₀ = f(x₀), и   Пусть также эти функции дифференцируемы:   Тогда их композиция также дифференцируема:   и её производная имеет вид:

Инвариантность формы первого дифференциала. Дифференциал функции z = g(y) в точке y₀ имеет вид: где dy — дифференциал тождественного отображения  : Пусть теперь   Тогда  , и согласно цепному правилу:

Таким образом, форма первого дифференциала остаётся одной и той же вне зависимости от того, является ли переменная функцией или нет.

13* производные высших порядков

 Если f '(x) — производная функции f (x), то производная от нее по независимой переменной x, (f '(x))' = f ''(x), называется производной второго порядка. Аналогично определены производные 3-го, 4-го, , и т.д, n-го порядка: f''' (x) = ( f'' (x))' , f (4)(x) = (f''' (x))' , f ⁽ⁿ⁾(x) = (f ^{(n -1)}(x))' . 14* неявная функция и ее дифференцирование

Пусть значения двух переменных (x) и (y) связаны между собой некоторым уравнением , которое мы запишем в виде F(x,y)=0      (2-94).   Это есть неявная функция т.к. (y) не выражено явно через (x). Так, например уравнение x²+y²-a²=0 (2-95). Неявно определяют следующие элементарные  и  (2-96) т.к. после подстановки в (2-95) имеем x²+(a²-x²)-a²=0 0=0 тождество. Замечание1. Термин ²явная² функция и ²неявная ² функция характеризуют не природу функции,  способ ее задания.

Правило. Дифференцирование неявной функции происходит по правилу нахождения производных, считая (x)-независимой переменной, а (y) – зависимой переменной. Пример. X²+y²-a²=0. Найдем производную. . Для примера продифференцируем функцию y= . 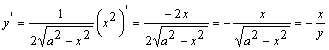, т.е. тоже самое. 15* дифференциалы высших порядков

Дифференциал высшего порядка функции одной переменной Для функции, зависящей от одной переменной второй и третий дифференциалы выглядят так:

Отсюда можно вывести общий вид дифференциала n-го порядка от функции   :

При вычислении дифференциалов высших порядков очень важно, что   есть произвольное и не зависящее от   , которое при дифференцировании по    следует рассматривать как постоянный множитель. Дифференциал высшего порядка функции нескольких переменных Если функция    имеет непрерывные частные производные второго порядка, то дифференциал второго порядка определяется так:  .

Символически общий вид дифференциала n-го порядка от функции   выглядит следующим образом:

где  а    произвольные приращения независимых переменных  . Приращения    рассматриваются как постоянные и остаются одними и теми же при переходе от одного дифференциала к следующему. Сложность выражения дифференциала возрастает с увеличением числа переменных.

16. теорема Ролля

Пусть ф-я f(x):

• Непрерывна на отрезке [a,b]

• Диф-ма, по крайней мере, в интервале (а,b)

• На концах отрезка принимает равные значения: f(a)=f(b)

Тогда между a и b найдется точка «с» (a<c<b), что f’(c)=0

Т. к ф-я непрерывна на отрезке [a,b], то по т.Вейерштресса, она принимает на этом отрезке как свое наибольшее зззначение М, так и наименьшее м. рассмотрим 2 случая:

1.М=м. в этом случае функция сохраняет постоянное значение. В самом деле их нер-ва м≤f(x)≤M следует, что f(x)=M=const. Следовательно f’(x)=0. ɎxC (a,b), и в качестве (^.)«с» можно взять любую из данного интервала.

2.М>м. т.к f(a)=f(b),то одно из значений ф-я принимает строго между a и b, т.е. в точке (^.) сC (a,b). Предположим, что f(c)=M, но если f(c) – наибольшее значение ф-и f(x), то ее приращение в точке с: ∆f(c)=f(c+∆x)-f(c)≤0 как при ∆х>0, так и при ∆х<0. Отсюда (∆f(c)/∆x)≤0. По условию теоремы ф-я имеет в точке с конечную производную, поэтому, переходя к пределу при ∆х 0, получаем:

1.lim ∆f(c)/∆x=f’(c)≤0

2.lim ∆f(c)/∆x=f’(c)≥0

И короче, выходит только f’(c)=0. Ура. Значит существует такая точка с, в которой производная f’(x)=0. 17. Теорема Лангранжа

Пусть ф-я f(x):

• Непрерывна на отрезке [a,b]

• Диф-ма, по крайней мере, в интервале (а,b)

Тогда между a и b найдется точка «с» (a<c<b), что справедливо рав-во

(f(b)-f(a))/b-a=f’(c) –формула Лангранжа

Рассмотрим вспомогательную ф-ю F(x)=f(x)-Rx где R-число. Подберем R так, чтобы выполнялось рав-во F(a)=F(b). Подставим F(x)=f(x)-Rx в рав-во F(a)=F(b)

F(a)-Ra=f(b)-Rb, Rb-Ra=f(b)-f(a), R=(f(b)-f(a))/b-a. теперь ф-я F(x)=f(x)-((f(b)-f(a))/b-a )*x удовлетворяет всем условиям теоремы Ролля.

• Она непрерывна на отрезке [a,b], т.к она представляет собой разность между непрерывной функцией f(x) и линейной ф-ей

• В интервале (a,b) она диф-ма и ее производная F’(x)=f’(x)-(f(b)-f(a))/b-a

• F(a)=F(b), чего мы добились подбором числа R

У-хо-хо, значит, найдется такая точка с С (a,b), в которой производная F’(x)=0.

F’(c)=0. Получается f’(c)-(f(b)-f(a))/b-a=0, f’(c)=(f(b)-f(a))/b-a. ура

18. теорема Коши

Пусть ф-и f(x) и g(x):

• Непрерывны на отрезке [a,b]

• Диф-мы, по крайней мере, в интервале (а,b)

• g’(x)≠0 в интервале (а,b)

тогда найдется такая точка сС(а,b), что справедлива формула (f(b)-g(a))/(g(b)-g(a))=f’(c)/g’(c) формула Коши

поехали: заметим, что g(b)≠g(a)! иначе по т.ролля в точке с внутри отрезка [a,b] производная g’(x)=0, а у нас условия. См выше. Рассмотрим вспомогательную функцию F(x)=f(x)-k*g(x). Естественно к-число. Подберем к так, чтобы выполнялось рав-во F(a)=F(b) Подставим F(x)=f(x)-к*g(x) в рав-во F(a)=F(b)

f(a)-k*g(a)=f(b)-k*g(b), k*(g(b)-g(a))=f(b)-f(a), k=(f(b)-f(a))/g(b)-g(a). теперь ф-я F(x)=f(x)-((f(b)-f(a))/g(b)-g(a) )*g(x) удовлетворяет всем условиям теоремы Ролля.

• Она непрерывна на отрезке [a,b], т.к f(x),g(x) непрерывны

• В интервале (a,b) она диф-ма, ее производная F’(x)=f’(x)-(f(b)-f(a))/g(b)-g(a)

• F(a)=F(b), чего мы добились подбором числа k

найдется такая точка с С (a,b), в которой производная F’(x)=0.

F’(c)=0.

Получается (f’(c)-(f(b)-f(a))/g(b)-g(a))*g’(c)=0, f’(c)/g’(c)=(f(b)-f(a))/g(b)-g(a).

19. правило Лопиталя. доказательство теоремы для случая непрерывности 0/0

Напоминаю, если lim f(x)=0 и lim g(x)=0, то говорят что дробь f(x)/g(x) является при х₀ 0 неопределенностью 0/0

Пусть ф-ии f(x) и g(x) удовлетворяют следующим условиям:

• f(x) и g(x) непрерывны в точке х₀ и в этой точке образуются в 0. f(x₀)=g(x₀)=0

• в окрестности точки х₀. За исключением самой х₀, ф-ии f(x) и g(x) диф-мы, причем g’(x)≠0

• следует конечный или бесконечный предел lim f’(x)/g’(x) (x x₀) тогда существует конечный или бесконечный предел lim f(x)/g(x) (x x₀) причем они равны (эти пределы). Это равенство и есть правило лопиталя

т.к. f(x₀)=g(x₀)=0, то справедливо f(x)/g(x)=(f(x)-f(x₀))/g(x)-g(x₀) к правой части применима т.Коши f(x)/g(x)=f’(p)/g’(p) p заключено между х₀ и х. перейдя в этом равенстве к пределу при х х₀, получим lim f(x)/g(x)= lim f’(p)/g’(p) (во2 пределе p 0). доказали)) ура)

20* формула Тейлора. остаточный член формулы Тейлора, его запись в форме Пеано и форме Лангранжа

Формула Тейлора 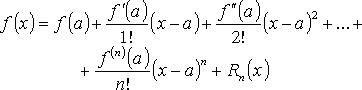 (R_n(x) - остаточный член формулы Тейлора). В форме Лагранжа:

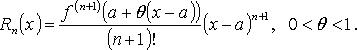
В форме Пеано:

 при 

21. возрастание и убывание функции. признаки монотонности

Функция f(x) наз-ся возрастающей на промежутке <a,b>, если для любых х₁<x₂, из этого промежутка выполняется нер-во f(x₁)<f(x₂). функция f(x) наз-ся убывающей на промежутке <a,b>, если для любых х₁<x₂, из этого промежутка выполняется нер-во f(x₁)>f(x₂). Если в определении возрастающей ф-ии строгое нер-во заменить на f(x₁)≤f(x₂), то на промежутке а,в ф-я наз-ся неубывающей. Т.о. возрастающая ф-я - частный случай неубывающей. Невозрастающая аналогично. Пусть ф-я f(x) непрерывна на отрезке [a,b] и диф-ма, по крайней мере, в интервале (a,b). Если во всех точках интервала (a,b) f’(x)>0, то ф-я f(x) возрастает на [a,b]. Рассмотрим 2 произвольных аргумента х₁,х₂ из [a,b], таких, что х₁<х₂. Тогда для ф-ии f(x) на [x₁,x₂] выполняются все условия т.Лагранжа. значит (f(x₂)-f(x₁))/x₂-x₁=f’(c), где с С (х₁,х₂). Отсюда, f(x₂)-f(x₁)= f’(c)*(x₂-x₁). По условию f’(c)>0. Т.к х₂-х₁>0,то f’(c)*(x₂-x₁)>0, а тогда f(x₂)-f(x₁)>0, f(x₁)< f(x₂). Итак, для любого х₁,x₂ из <a,b> следует f(x₁)< f(x₂), т.е ф-я возрастает на [a,b]. Аналогично док-ся и след. Теорема: Пусть ф-я f(x) непрерывна на отрезке [a,b] и диф-ма, по крайней мере, в интервале (a,b). Если во всех точках интервала (a,b) f’(x)<0, то ф-я f(x) убывает на [a,b]. 22. экстремумы функции. теорема Ферма. критические точки. первый достатоный признак экстремума

Пусть ф-я f(x) задана на промежутке <a,b> и x₀-внутренняя точка этого промежутка. Говорят, что ф-я имеет в точке х₀ максимум, если существует такая окрестность точки х₀, что для любого х≠х₀ из этой окрестности выполняется нер-во f(x)<f(x₀). Пусть ф-я f(x) задана на промежутке <a,b> и x₀-внутренняя точка этого промежутка. Говорят, что ф-я имеет в точке х₀ минимум, если существует такая окрестность точки х₀, что для любого х≠х₀ из этой окрестности выполняется нер-во f(x)>f(x₀). Т.Ферма если ф-я имеет в точке экстремума конечную производную, то эта производная обязательно равна нулю. Из т.следует, что точки, в которых ф-я имеет экстремумы, следует искать среди тех внутренних точек ее области задания, где либо f’(x)=0, либо f’(x)=∞, либо f’(x) не существует. Точки указанного вида наз-ся критическими точками. Но не в каждой критической точке будт экстремум. 1-ый достаточный признак экстремума: пусть х₀-критическая точка, и ф-я f(x) непрерывна в точке х₀, диф-ма в окрестности этой точки. За исключение. Быть может, самой точке х₀. Если при переходе х черех точку х₀ производная f’(x) меняет знак, то ф-я имеет экстремум в точке х0ж при этом она имеет максимум, если производная меняет знак с + на – и минимум, если производная меняет знак с – на +. В док-во нужно рисовать графики, что я делать не буду. 23. второй достаточный признак экстремума

Если в точке x₀ первая производная f '(x) функции f(x) обращается в нуль, а её вторая производная f ''(x) отлична от нуля, то в точке x₀ функция f(x) достигает экстремума (минимума, если f ''(x) > 0, и максимума, еслиf ''(x) < 0). Предполагается, что f ''(x) непрерывна в точке x₀ и ее окрестности. Д оказательство. Докажем необходимость условия существования максимума. Пустьf '(x) = 0,  f ''(x) > 0. Так как f ''(x) непрерывна, то в достаточно малом интервале (x₀ - h, x₀ + h) вторая производная положительна: f ''(x) > 0. Это означает, что f '(x) возрастает в этом интервале. Так как при этомf '(x₀ )=0, то f '(x)<0 в интервале (x₀ - h, x₀ ) и f '(x)>0 в интервале (x₀  , x₀ + h). Таким образом, функция f(x) убывает в интервале (x₀ - h, x₀ ) и возрастает в интервале (x₀  , x₀ + h). Поэтому в точке x₀ функция f(x) имеет минимум. Аналогично доказывается достаточность условия существования максимума. На рисунке функция f(x) имеет в точке x₁ минимум, в точке x₂ - максимум. Второй производной можно воспользоваться при решении задач на отыскание максимума и минимума функции. 24. направление изгиба кривой. достаточные условия выпуклости и вогнутости

25* точки перегиба кривой. признак наличия или отсутствия перегиба в точке

Точка перегиба плоской кривой — это точка кривой, в которой ее кривизна меняет знак. Для графика функции, это эквивалентно тому, что знак меняет вторая производная функции.