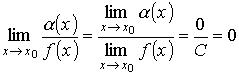Доказательство.
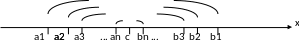 Левые концы отрезков последовательности
(1) образуют неубывающую последовательность:
Левые концы отрезков последовательности
(1) образуют неубывающую последовательность:
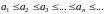 ,
а правые концы – невозрастающую
последовательность:
,
а правые концы – невозрастающую
последовательность:
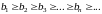 Так как
Так как
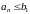 ,
то
,
то
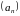 – ограничена сверху; так как
– ограничена сверху; так как
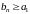 то
то
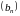 - ограничена снизу.
- ограничена снизу.
Так как
- неубывающая и ограничена сверху, то
по теореме 1 § 7 она имеет предел:
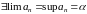 ,
причем
,
причем
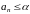 . (2)
. (2)
По теореме 1 § 7
 ,
,
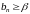 . (3)
. (3)
Тогда из соотношения
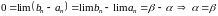 .
.
Общее значение a и b обозначим через с. Из (2), (3) следует, что , то есть точка с принадлежит всем отрезкам последовательности (1).
П окажем,
что с единственная точка, принадлежащая
всем отрезкам последовательности (1).
Допустим противное. Пусть $точка
с1¹с:
окажем,
что с единственная точка, принадлежащая
всем отрезкам последовательности (1).
Допустим противное. Пусть $точка
с1¹с:
 .
Следовательно,
должно выполняться неравенство
.
Следовательно,
должно выполняться неравенство
 ,
значит,
,
значит,
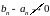 ,
что противоречит условию теоремы.
,
что противоречит условию теоремы.
Подпоследовательности. Теорема Больцано-Вейерштрасса.
Рассмотрим последовательность
 (1)
(1)
Выберем произвольную возрастающую
последовательность натуральных чисел
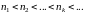
Выберем из последовательности (1) члены
с номерами
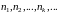 ,
получим последовательность
,
получим последовательность
 (2)
(2)
Последовательность (2) называется подпоследовательностью (или частичной последовательностью) последовательности (1).
Теорема 2. (Больцано-Вейерштрасса) Из всякой ограниченной последовательности можно выделить сходящуюся подпоследовательность.
Доказательство.
Пусть (1) - ограниченная последовательность, то есть
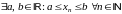 .
.
Рассмотрим отрезок
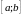 ,
он содержит все члены последовательности
(1).
,
он содержит все члены последовательности
(1).
Положим,
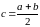 ,
длина
,
длина
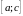 равна
длине
равна
длине
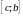 .
По крайней мере, один из них содержит
бесконечно много членов последовательности
(доказательство от противного), обозначим
его
.
По крайней мере, один из них содержит
бесконечно много членов последовательности
(доказательство от противного), обозначим
его
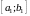 .
(Если окажется, что оба отрезка содержат
бесконечное число членов (1), то выбираем
любой из них).
.
(Если окажется, что оба отрезка содержат
бесконечное число членов (1), то выбираем
любой из них).
Отрезок
делим на 2 равные части и через
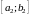 обозначаем ту из них, которая содержит
бесконечное множество число членов
последовательности (1). Продолжая этот
процесс неограниченно, мы получим
последовательность вложенных отрезков:
(3)
обозначаем ту из них, которая содержит
бесконечное множество число членов
последовательности (1). Продолжая этот
процесс неограниченно, мы получим
последовательность вложенных отрезков:
(3)
Каждый отрезок содержит бесконечно много членов последовательности (1).
Последовательность (3) является
стягивающейся, так как
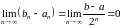 .
Следовательно, по теореме § 8 существует
единственная точка с, принадлежащая
всем отрезкам последовательности (3),
то есть
,
.
Следовательно, по теореме § 8 существует
единственная точка с, принадлежащая
всем отрезкам последовательности (3),
то есть
,
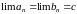 .
.
Построим подпоследовательность
 последовательности (1), сходящуюся к
числу с
последовательности (1), сходящуюся к
числу с
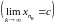 ,
следующим образом. Возьмем какой-нибудь
из членов последовательности (1),
содержащийся на
и обозначим его
,
следующим образом. Возьмем какой-нибудь
из членов последовательности (1),
содержащийся на
и обозначим его
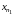 ,
на
возьмем какой-либо член последовательности
(1) и обозначим его
,
на
возьмем какой-либо член последовательности
(1) и обозначим его
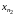 и так далее. Это всегда можно сделать,
так как все эти отрезки содержат
бесконечно много членов последовательности(1).
Получим подпоследовательность
и так далее. Это всегда можно сделать,
так как все эти отрезки содержат
бесконечно много членов последовательности(1).
Получим подпоследовательность
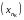 последовательности (1).
последовательности (1).
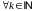
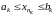 ,
так как
,
так как
 ,
то по теореме о пределе промежуточной
последовательности
,
то по теореме о пределе промежуточной
последовательности
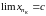 .
.
![]()
Фундаментальные последовательности. Критерий Коши.
Фундаментальные последовательности. Теорема о фундаментальности сходящейся последовательности.
Определение.
Последовательность
(xn)
называется фундаментальной,
если
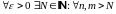 выполнено
выполнено
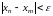 . (1)
. (1)
Теорема (критерий Коши сходимости числовой последовательности)
Последовательность сходится тогда и только тогда, когда она фундаментальна.
Доказательство.
1) Необходимость.
Пусть
(xn)
сходится, т.е. $
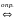 Þ
Þ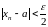 (2)
(2)
Возьмем "m>N,
для него тоже выполнено неравенство
(2):
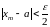 .
Тогда
.
Тогда
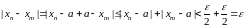 .
.
Следовательно (по определению) (xn) фундаментальна.
2) Достаточность.
Пусть (xn) фундаментальна, т.е. Þ .
Отсюда xm-e<xn<xm+e
"n>N.
Т.е., начиная с номера N+1,
последовательность ограничена. Выберем
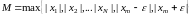 .Тогда
.Тогда
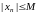 ,
т.е. последовательность (xn)
ограничена.
Следовательно, по теореме Больцано-Вейерштрасса
из нее можно выделить сходящуюся
подпоследовательность
:
,
т.е. последовательность (xn)
ограничена.
Следовательно, по теореме Больцано-Вейерштрасса
из нее можно выделить сходящуюся
подпоследовательность
:
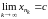 .
Покажем, что тогда и
.
Покажем, что тогда и
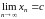 .
.
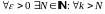 Þ
Þ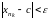 ,
и одновременно nk>N.
,
и одновременно nk>N.
Т.к. в неравенстве
(1) m>N,
то возьмем в нем m=nk,
получим
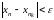 .
.
Тогда
 "n>N.
Это означает, что
,
т.е. последовательность (xn)
сходится.
"n>N.
Это означает, что
,
т.е. последовательность (xn)
сходится.
Определение числа e.
Лемма (неравенство Бернулли)
,
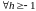 выполняется
выполняется
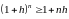 .
.
Доказательство.
(Методом математической индукции)
1) n=1:
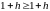 -
верно.
-
верно.
2) Пусть неравенство верно для n=k,
то есть
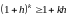 .
Докажем, что оно верно и для n=k+1.
Умножим обе части на 1+h.
Так как
.
Докажем, что оно верно и для n=k+1.
Умножим обе части на 1+h.
Так как
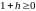 ,
то
,
то
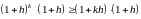 .
Раскроем справа скобки:
.
Раскроем справа скобки:
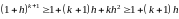 ,
так как
,
так как
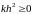 .
.
То есть неравенство верно для n=k+1.
Из 1), 2) следует, что , выполняется .
Рассмотрим последовательность
:
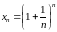 .
Докажем, что она имеет предел.
.
Докажем, что она имеет предел.
1) Рассмотрим последовательность
:
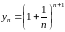 .
.
Докажем, что она имеет предел. Для этого покажем, что
а) не возрастает,
б) ограничена снизу.
а)
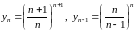
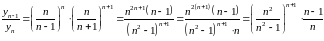 ;
;
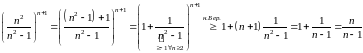 Тогда
Тогда
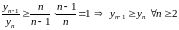 ,
следовательно,
не возрастает.
,
следовательно,
не возрастает.
б)
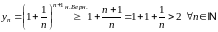 ,
значит,
ограничена снизу.
,
значит,
ограничена снизу.
Из а) и б)
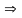 что
имеет предел (по теореме 1 § 7).
что
имеет предел (по теореме 1 § 7).
2)
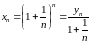 .
.
Так как
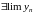 и
и
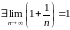 ,
то
,
то
 .
.
Этот предел принято обозначать буквой е:
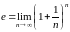 .
.
е- иррациональное число, впервые введенное Эйлером (1707-1783).
е=2,718281828459045…
Предел функции. Эквивалентность двух определений.
Теорема 1. Первое и второе определения предела функции в точке прикосновения множества определения функции эквивалентны.
Доказательство. Докажем, что если функция имеет в некоторой точке предел по Гейне, то она имеет тот же самый предел в этой точке и по Коши. Пусть
 ,
x0 – точка прикосновения множества X и
,
x0 – точка прикосновения множества X и
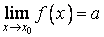 в
смысле первого определения предела
функции.
в
смысле первого определения предела
функции.Ограничимся здесь случаем конечных x0 и a. Допустим, что предел по Коши не совпадает с пределом по Гейне, т. е.
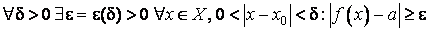 . (12.1)
. (12.1)Возьмём
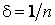 .
Выберем в каждой такой -окрестности
точки x0 элемент xn. Тогда, по построению,
имеем последовательность
.
Выберем в каждой такой -окрестности
точки x0 элемент xn. Тогда, по построению,
имеем последовательность
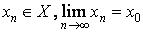 .
При этом, в силу (4), все элементы
последовательности
.
При этом, в силу (4), все элементы
последовательности
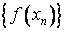 лежат
вне
-окрестности
точки a.
лежат
вне
-окрестности
точки a.С другой стороны, поскольку в смысле первого определения, то для любой последовательности имеет место равенство
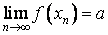 .
Согласно определению предела
последовательности это означает, что
для любой окрестности точки a, в частности
и для выбранной выше -окрестности,
существует такой номер N, что для всех
номеров n>N имеет место
.
Согласно определению предела
последовательности это означает, что
для любой окрестности точки a, в частности
и для выбранной выше -окрестности,
существует такой номер N, что для всех
номеров n>N имеет место
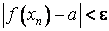 .
.Полученное противоречие доказывает сделанное утверждение. □
Теперь докажем, что если функция имеет в некоторой точке предел в смысле второго определения, то она имеет в этой точке тот же самый предел и в смысле первого определения. Пусть в смысле предела функции по Коши, , x0 – предельная точка множества X, и пусть
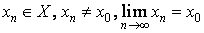 .
Покажем, что тогда
,
т. е. точка a является пределом функции
f и в смысле определения предела функции
по Гейне.
.
Покажем, что тогда
,
т. е. точка a является пределом функции
f и в смысле определения предела функции
по Гейне.Зададим произвольную -окрестность точки a. Тогда, по условию теоремы,
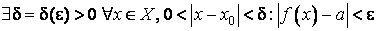 . (12.2)
. (12.2)Для этой -окрестности найдётся такой номер N, что для всех номеров n>N будет выполняться условие
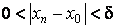 .
Но тогда, в силу (5), имеем
.
Это и означает, что
.
.
Но тогда, в силу (5), имеем
.
Это и означает, что
.Если же x0 – изолированная точка множества X, то функция f непрерывна в этой точке (почему?) и имеет место равенство
 .
.
Свойства пределов функций, выражаемые неравенствами.
Обозначение предела
Предел
функции обозначается как
![]() или
через символ предела:
или
через символ предела:
![]() .
Всюду ниже предполагается, что
пределы функций
.
Всюду ниже предполагается, что
пределы функций
![]() существуют.
существуют.
Предел суммы
Предел суммы двух функций равен сумме пределов этих функций:
![]()
Расширенное правило суммы
![]()
![]()
Предел произведения
Предел произведения двух функций равен произведению пределов этих функций (при условии, что последние существуют):
![]()
Расширенное правило произведения
![]()
Предел частного
Предел частного двух функций равен отношению пределов этих функций при условии, что предел знаменателя не равен нулю:

Предел степенной функции
![]()
где степень p - действительное число. В частности,
![]()
Если f ( x ) = x, то
![]()
Предел показательной функции
![]()
где основание a > 0.
Предел логарифмической функции
![]()
где основание a > 0.
Бесконечно малые функции и их свойства.
Функция f (x) называется бесконечно малой функцией в точке х = х0, если
![]()
Аналогично определяются бесконечно малые функции при x → ∞, x → + ∞, x → – ∞, x → x0 – 0, x → x0 + 0. Можно дать равносильное определение бесконечно малой функции «на языке ε – δ: функция f (x) называется бесконечно малой в точке х = х0, если для любого как угодно малого ε > 0 существует δ = δ(ε) > 0, такое, что для всех х, удовлетворяющих неравенству 0 < | х – x0 | < δ, выполняется неравенство | f (x) | < ε. Или в символьном виде
(![]() ε > 0) (
ε > 0) (
![]() δ
= δ(ε) > 0)(
0
< |х – х0| < δ ) : | f
(x) | < ε.
δ
= δ(ε) > 0)(
0
< |х – х0| < δ ) : | f
(x) | < ε.
Опираясь на правила вычисления пределов, можно сформулировать свойства бесконечно малых: алгебраическая сумма и произведение конечного числа бесконечно малых функций при x → x0, а также произведение бесконечно малой функции на ограниченную функцию являются бесконечно малыми функциями при x → x0:
1. |
|
2. |
|
3. |
|
4. |
|
Все сказанное о бесконечно малых функциях при x → x0 справедливо и для бесконечно малых функций при x → ∞, x → + ∞, x → – ∞, x → x0 – 0, x → x0 + 0.
Арифметические свойства пределов функций.
Арифметические свойства предела функции в точке.
Если функции f1(x) и f2(x) имеет точке х0 предел А1 и А2, то функции f1(x) + f2(x), f1(x) f2(x), f1(x) / f2(x) имеют пределы А1 + А2, А1А2, А1/ А2.
Теорема о пределе сложной функции.
Пусть числовые функции f (x) и g (x) определены на некотором интервале, быть может, кроме точки х0 этого интервала, и имеют конечные пределы в этой точке
![]() и
и
![]()
Тогда
если | A | < ∞, то функция f (x) ограничена в окрестности точки х0. Доказательство. Так как
![]()
то
( ε > 0 ) ( δ = δ (ε) > 0 ) ( 0 < | x - x0 | < δ ) : | f (x) − A | < ε
Из этого определения следует ограниченность функции: A - ε < f (x) < A + ε в окрестности x0– δ < x < x0 + δ, что и требовалось доказать.
Односторонние пределы, связь с пределом функции.
Односторо́нний преде́л — предел числовой функции, подразумевающий «приближение» к предельной точке с одной стороны. Такие пределы называют соответственно левосторо́нним преде́лом (или преде́лом сле́ва) и правосторо́нним преде́лом (преде́лом спра́ва)
Монотонные функции. Теорема о пределе монотонной функции.
Функция называется возрастающей на отрезке [а, b], принадлежащем области определения функции, если любому большему значению аргумента из этого отрезка соответствует большее значение функции
x2
> x1→
f (x2)
> f (x1)
х1,
x2
![]() [a,
b].
[a,
b].
Функция называется убывающей на отрезке [a, b], если любому большему значению аргумента из этого интервала соответствуют меньшие значения функции
x2 > x1→ f (x2) < f (x1) х1, x2 [a, b].
Функции, убывающие или возрастающие на некотором числовом промежутке, называются монотонными функциями. Участки возрастания функции на рисунке отмечены синим цветом (в чёрно белом варианте более толстым форматом).
Пусть функция
![]() —
монотонна и ограничена в проколотой
окрестности точки
—
монотонна и ограничена в проколотой
окрестности точки
![]() .
Тогда в этой точке у функции существует
односторонний предел.
.
Тогда в этой точке у функции существует
односторонний предел.
Доказательство:
![]()
Рассмотрим левосторонний предел и будем считать, что функция возрастает.
Так как
—
ограничена, то
![]() .
.
Докажем, что
![]() ,
используя свойства
,
используя свойства
![]() .
.
![]()
Тогда так как
![]() ,
тогда для таких
,
тогда для таких
![]() .
.
В
качестве
![]() можно
брать
можно
брать
![]() ,
тогда предел существует по определению.
,
тогда предел существует по определению.
![]()
Первый замечательный предел и его следствия

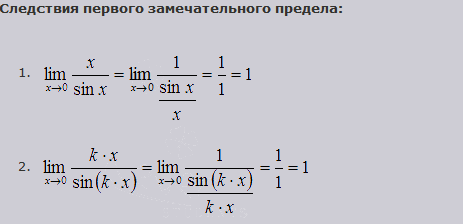
Второй замечательный предел и его следствия.
![]() или
или
![]()
Следствия
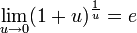
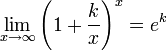
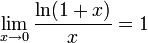
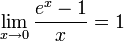
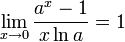 для
для
 ,
,
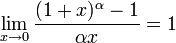
Непрерывные функции. Свойства непрерывных функций, выражаемые неравенствами и равенствами.
Функцию y = f(x) называют непрерывной на отрезке [a, b], если она непрерывна во всех внутренних точках этого отрезка, а на его концах, т.е. в точках a и b, непрерывна соответственно справа и слева.
Свойства непрерывных функций.
1) Сумма, разность и произведение непрерывных в точке х0 функций – есть функция, непрерывная в точке х0.
2) Частное двух непрерывных функций
![]() –
есть непрерывная функция при условии,
что g(x) не
равна нулю в точке х0.
–
есть непрерывная функция при условии,
что g(x) не
равна нулю в точке х0.
3) Суперпозиция непрерывных функций – есть непрерывная функция.
Это свойство может быть записано следующим образом:
Если u = f(x), v = g(x) – непрерывные функции в точке х = х0, то функция v = g(f(x)) – тоже непрерывнаяфункция в этой точке.
Теорема о непрерывности и разрывах монотонной функции.
Непрерывность и разрывы монотонной функции.
Теор.5.5.1. Пусть функция f(x) определена на отрезке [a,b] и монотонна на этом отрезке. Тогда f(x) может иметь на этом отрезке только точки разрыва первого рода.
Док-во. Рассмотрим для определённости
случай монотонно возрастающей функции.
Пусть х0[a,b] и не
является левым концом этого отрезка.
Рассмотрим полуинтервал [a, х0). В разделе
4.3.2. Свойства сходящейся последовательности
мы доказали, что монотонно возрастающая
ограниченная сверху последовательность
имеет предел. Совершенно также можно
доказать, что функция, монотонно
возрастающая на полуинтервале [a, х0),
множество значений которой ограничено
на этом интервале, обязана иметь
![]() .
Действительно, так как множество
.
Действительно, так как множество
![]() ограничено
сверху (одна из верхних границ - значение
f(х0)), оно имеет верхнюю грань М*, обладающую
тем свойством, что для 0
х1[a,
х0), в котором f(х1)
М* .
По монотонности функции и по определению
верхней грани для х:
х1х
х0 справедливо неравенство М*
f(х1)
f(х) М*, что означает
выполнение условий существования
ограничено
сверху (одна из верхних границ - значение
f(х0)), оно имеет верхнюю грань М*, обладающую
тем свойством, что для 0
х1[a,
х0), в котором f(х1)
М* .
По монотонности функции и по определению
верхней грани для х:
х1х
х0 справедливо неравенство М*
f(х1)
f(х) М*, что означает
выполнение условий существования
![]() с
= х0- х1. При этом
возможны два варианта: либо f(х0)=М*, тогда
f(х) непрерывна слева в точке х0; либо
f(х0)М*, тогда f(х)
имеет в точке х0 скачок, т.е. разрыв
первого рода.
с
= х0- х1. При этом
возможны два варианта: либо f(х0)=М*, тогда
f(х) непрерывна слева в точке х0; либо
f(х0)М*, тогда f(х)
имеет в точке х0 скачок, т.е. разрыв
первого рода.
Следствие: если множество значений монотонно возрастающей на отрезке [a,b] функции f(х) полностью заполняет отрезок [f (a), f( b)] (т.е. для у[f (a), f( b)] х[a,b] такой, что f(х)= у), то эта функция непрерывна, легко доказать теперь от противного. Если в точке х0 имеется скачок, то f(х) не может принимать значений, попадающих в интервал (f(х0-0), f(х0)).
Ограниченные функции. Первая теорема Вейерштрасса.
Первая теорема Вейерштрасса: если функция f(x) непрерывна на [a,b], то она ограничена на этом отрезке.
Так как по условию функция f(x) непрерывна на [a,b], то она непрерывна в каждой точке этого отрезка.
![]() .
.
![]()
![]()
Семейство этих интервалов будет представлять собой покрытие отрезка [a,b].
В силу принципа Бореля-Лебега из этого покрытия отрезка [a,b] можно выделить конечное подпокрытие:
![]()
![]()
![]()
Пусть m=min{![]() },
},
M=max{![]() }/
}/
Тогда
![]() .
Теорема доказана.
.
Теорема доказана.
Вторая теорема Вейерштрасса.
Вторая теорема Вейерштрасса о достижении
непрерывной функцией своего наибольшего
и наименьшего значений: если функция
f(x) непрерывна на [a,b], то найдется такая
точка
![]() ,
в которой функция достигает своего
максимума, найдется такая точка
,
в которой функция достигает своего
максимума, найдется такая точка
![]() ,
в которой функция достигает своего
минимума.
,
в которой функция достигает своего
минимума.
Доказательство:
Пусть функция f(x) непрерывна на [a,b], тогда в силу теоремы 1 она ограничена на этом отрезке. Следовательно, ограничено множество значений функции. Тогда в силу принципа верхней грани это множество обладает точной верхней и точной нижней границами.
Обозначим:
![]() и
покажем, что
и
покажем, что
![]() и
будет наибольшим значением функции
f(x) на отрезке [a,b]:
и
будет наибольшим значением функции
f(x) на отрезке [a,b]:
![]() .
.
Предположим противное, то есть
![]() .
.
Так как , то f(x)< .
-f(x)>0
введем в рассмотрение функцию
![]() .
Функция
.
Функция
![]() непрерывна
на [a,b], так как
-f(x)
непрерывна
на [a,b], так как
-f(x)![]() 0.
Тогда, в силу первой теоремы Вейерштрасса,
функция
ограничена
на [a,b].
0.
Тогда, в силу первой теоремы Вейерштрасса,
функция
ограничена
на [a,b].
![]() <M
<M
![]() >
>![]()
![]() ,
где
,
где
![]() >0
>0