anal

Линейная алгебра и аналитическая геометрия

1. Понятие числового поля. Аксиоматика, основные свойства операций + и *

Поле - множество элементов, для которых определены арифметические операции.

Для полей верны следующие утверждения:

a) Для любых элементов a и b поля F определены их сумма a+b и произведение a*b

b) Выполняются следующие тождества:

1) x+y=y+x

2) x+(y+z)=(x+y)+z

3) Существует 0 (нейтральный элемент), т.ч. x+0=x

4) Для любого x существует –х (противоположный элемент), т.ч. x+(-x)=0

5) xy=yx

6) (xy)z=x(yz)

7) Существует 1 (единица): x*1=x;

8) Для любого x не равного 0 существует 1/x (x^-1, обратный элемент): x*(1/x)=1

9) (x+y)z=xz+yz

Свойство полей: в любом поле нет делителя ноля

Доказательство: ab=0; a=0 или b=0;

Если a!=0, то существует обратный элемент a^-1: aa^-1=1

a^-1(ab)=a^-1*0=0

(a^-1*a)b=0

1*b=0=>b=0

2. Комплексные числа. Действия над ними.

Ко́мпле́ксные чи́сла — расширение множества вещественных чисел, обычно обозначается . Любое комплексное число может быть представлено как формальная сумма x + iy, где x и y — вещественные числа, i — мнимая единица. (wiki)

z = a+bi; i - мнимая единица

z̅ = a-bi;

Действия надо комплексными числами:

Потом все выражается через их представление как z=a+bi. Остальные операции (+ - *) делаются тривиально

Возведение в степень:

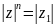
Основная теорема алгебры: Любые уравнения n-ной степени над комплексными числами имеют n корней

2. Многочлены над полем. Деление многочленов (алгоритм Эвклида). Теорема Безу. Разложение многочленов над полями действительных и комплексных чисел на простейшие множители.

Многочлен -

Все многочлены рассматриваются над полем F=C

Т.е. =>

Деление многочленов

Лемма. Число является корнем многочлена тогда и только тогда, когда делится на (x-b)

, где (x-b)=r(x) – делитель, g(x) – частное, h(x) – остаток

(Алгоритм Евклида (Эвклида О_о)

Теорема Безу

Теорема Безу утверждает, что остаток от деления многочлена P(x) на двучлен x − a равен P(a).

Доказательство

Поделим с остатком многочлен P(x) на многочлен x − a:

P(x) = (x − a)Q(x) + R(x).

Так как deg R(x) < deg(x − a) = 1, то R(x) — многочлен степени не выше 0. Подставляя x = a, поскольку (a − a)Q(a) = 0, имеем P(a) = R(a).

Любой многочлен с действительными коэффициентами раскладывается на произведение линейных множителей в виде (х-р), где р-действительное и квадратных трехчленов с действительными коэффициентами, не имеющих корней

2. Матрицы, сложение, умножение их. Умножение матриц на числа. Свойства этих операций.

Матрица – прямоугольная таблица, состоящая из n строк и m столбцов. - элемент матрицы.

Матрица, количество строк и столбоцов которой равны n называется квадратной матрицей порядка n

Диагональ, идущая от левого верхнего к правому нижнему углу называется главной диагональю.

Матрица называется единичной, если элементы ее главной диагонали равны единицам, а остальные – нулям.

Тут непонятная последовательность символов из тетради:

(Вот такая вот хрень)

Сложение матриц

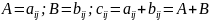
Умножение матрицы на число

Свойства:

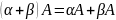
Еще свойства (из другого места)

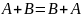
Умножение матрицы на матрицу

определено только если m=p и

То есть для нахождения элемента конечной матрицы, мы складываем произведения элементов перемножаемых матриц, причем в 1 матрице мы движемся вниз по столбцу, а во 2 матрице – вправо по строке

(свойств у меня нету, кто найдет – дополните)

2. Определитель матрицы, свойства определителей

Определитель (детерминант) матрицы – общий знаменатель значений переменных.

Для матрицы второго порядка (2х2) он равен разности произведений элементов главной и второй диагоналей:

И называется определителем второго порядка (матрицы второго порядка)

Определитель 3-го порядка:

Определитель n-го порядка:

Минором элемента матрицы A называется определитель матрицы, полученной из A вычерком i-той сторки и j-того столца.

Алгебраическим дополнением элемента матрицы А называется число

Определитель для матрицы A (та что сверху)

Строку для нахождения определителя выбираем сами. Рациональнее, если в ней как можно больше нулей будет=)

Свойства определителей

1. Если матрица имеет нулевую строчку/столбец, то ее определитель равен нулю.

2. Если в матрице поменять местами любые 2 строки (стобца), то определитель меняет знак

3. Если в матрице есть две одинаковых строки (столбца), ее определитель равен 0

4. Общий множитель элементов любой строки (столбца) может быть вынесен за знак определителя:

5. Если в матрице есть две пропорциональных строки (стобца), ее определитель равен 0

6. 

7. Транспонирование: получается из A заменой ее столбцов на строки с сохранением их порядка ( ).

2. Обратные матрицы

Применительно к уравнениям:

Элементарные преобразования матрицы:

- Можно менять местами любые две строки

- Можно умножать любую строку на любое ненулевое число

- Можно элементы некоторой строки сложить с элементами другой строки, помноженной на некоторое фиксированное число

Получение обратной матрицы (методом кого то там)

2. Системы линейных уравнений. Решение их методами Крамера, с помощью обратной матрицы и методом Гаусса.

Метод Крамера:

1) Если определитель системы Δ не равен 0, то система имеет одно единственное решение:

2) Если Δ=0, но какое –то из не равно нулю, то решений у системы нет

3) Если то либо система не имеет решений, либо решений бесконечно много.

С помощью обратной матрицы

Т.е. систему можно записать так: AX=B

Если

Метод Гаусса:

Приводим полученную матрицу с помощью элементарных преобразований к следующему виду:

На месте * может быть либо 1 либо 0, на месте ? любое число, включая 0.

Полученная матрица может принять следующие характерные формы:

– одно решение

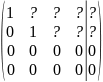– бесконечно много решений

– решений нет

2. Однородные системы линейных уравнений, фундаментальная система решений подобных систем. Взаимосвязь решений неоднородной системы с решениями соответствующей однородной

Система

Называется однородной, если все ее свободные члены (b1=…=bn=0)

Свободные неизвестные – неизвестные, которые равны нулю

Допустим, есть система:

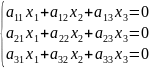
Матрица:

(допустим, мы получили что то подобное в процессе преобразований)

Очевидно, что 1 и 2 столбцы линейно независимы, а остальные являются их линейными комбинациями. Поэтому 1 и 2 столбцы – базисные.

Так как количество линейно независимых столбцов A = 2 то Rg A = 2 (ранг)

Следовательно, размерность подпространства решений d=n-r, где n-количество неизвестных, r – ранг матрицы.

В данном случае оно равно 1.

Запишем систему уравнений из Гауссовой матрицы (та, к которой привели)

Полагая, что = 1, находим фундаментальное решение системы:

И общее решение однородной системы:

Если независимых неизвестных больше, аналогично получаем другие элементы подпространство, принимая каждую независимую неизвестную за произвольное ненулевое число (1), а остальные за 0. И получаем в общем виде для n-мерного подпространства решений:

Где – базис подпространства решений, а – произвольные числа

Взаимосвязь решений неоднородной системы с решениями соответствующей однородной.

Значица сначала (или потом) решаем однородную систему (свободные члены заменяем нулями) и получаем базис решения:

Потом находим решение системы (как обычной системы) X (если есть свободные неизвестные, приравниваем их к 0)

И вот мы получили решение системы:

2. Сложение геометрических векторов. Умножение их на числа. Свойства этих операций.

Сложение:

Свойства:

(сложение проекций)

Умножение вектора на число:

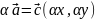
Свойства:

(Ассоциативность)

(Дистрибутивность умножения относительно сложения чисел)

(Дистрибутивность умножение относительно сложения векторов)

2. Скалярное произведение геометрических векторов: определение , свойства, формулы для вычислений

Скаля́рное произведе́ние — операция над двумя векторами, результатом которой является скаляр (число), не зависящее от системы координат и характеризующее длины векторов-сомножителей и угол между ними. (wiki)

Свойства скалярного произведения:

1. 

2. 

3. 

4. 

5. 

Формулы умножения:

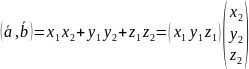
2. Векторное произведение векторов: определение, свойства, формула для вычисления

Векторное произведение — это псевдовектор, перпендикулярный плоскости, построенной по двум сомножителям, являющийся результатом бинарной операции «векторное умножение» над векторами в трёхмерном Евклидовом пространстве. Произведение не является ни коммутативным, ни ассоциативным (оно является антикоммутативным) и отличается от скалярного произведения векторов. Во многих задачах инженерии и физики нужно иметь возможность строить вектор, перпендикулярный двум имеющимся — векторное произведение предоставляет эту возможность. Векторное произведение полезно для «измерения» перпендикулярности векторов — длина векторного произведения двух векторов равна произведению их длин, если они перпендикулярны, и уменьшается до нуля, если векторы параллельны. (wiki)

Или

Описание векторного произведения:

1. 

2. 

Свойства векторного произведения:

1. 

2. 

3. 

4. 

5. 

6. Формула вычисления:

2. Смешанное произведение. Определение, свойства, формула для вычисления.

Определение:

Свойства:

1. 

2. 

⇒ 3)

4)

5)

6)

2. Плоскости. Их уравнения. Основные задачи, связанные с плоскостями

Общее уравнение плоскости:

Ax + By + Cz + D = 0; причем A, B, C не могут быть равну нулю одновременно

Уравнение плоскости в векторной форме:

Уравнение плоскости в отрезках:

Где – отрезки, отсекаемые плоскостью на осях Ox, Oy, Oz

Уравнение плоскости, проходящей через точку перпендикулярно вектору нормали N(A, B, C):

Уравнение плоскости, проходящей через три заданные точки  , не лежащие на одной прямой:

(смешанное произведение векторов), иначе

Примеры решения задач: википедия=)