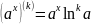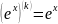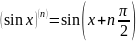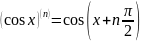- •Свойства модуля:
- •Числовая последовательность
- •Предел числовой последовательности
- •Свойства сходящихся последовательностей:
- •Верхний и нижний пределы последовательности.
- •Точки сгущения (предельные точки).
- •Определение предела функции по Гейне и Коши
- •Дифференцируемость функции в точке. Дифференциал функции. Его геометрический и физический смыслы.
- •Основные формулы дифференцирования элементарных функций.
- •Уравнение касательной прямой, в кривой, заданной параметрически.
- •3 Класса точек параметрически заданной кривой:
- •Гладкие функции и гладкие кривые на плоскости.
- •Старшие производные и дифференциалы функций.
- •Производные и дифференциалы старших порядков для сложных функций.
- •Теоремы о среднем для дифференцируемых функций.
- •Вычисление пределов с помощью правил Лопиталя.
- •Исследование локальных экстремумов функции.
- •Нахождение глобального экстремума функции на отрезке.
- •Асимптоты функции. Горизонтальные, вертикальные, наклонные.
Гладкие функции и гладкие кривые на плоскости.
Опр.
Функцию
называют принадлежащей к классу
 на
множестве Х,
если функция
имеет на множестве Х
производную и эта производная является
непрерывной функцией
на
множестве Х,
если функция
имеет на множестве Х
производную и эта производная является
непрерывной функцией
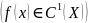 .
.
Графиком этой функции является некоторая кривая (линия) на плоскости, в каждой точке которой существует касательная и положение этой касательной непрерывно меняется. Такие кривые называют гладкими кривыми
Графики всех элементарных функций являются гладкими кривыми в своих областях определения.
Опр. Непрерывную функцию называют кусочно гладкой функцией, если она в каждой точке имеет производную, которая непрерывно изменяется, за исключением конечного числа точек, в которых производная терпит разрыв I рода.
Опр.
Кривую Г на плоскости, заданную
параметрически,
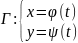 называют
гладкой кривой на плоскости, если
выполняются следующие условия:
называют
гладкой кривой на плоскости, если
выполняются следующие условия:
Кривая Г задается непрерывно дифференцируемой параметризацией.
Все точки на этой кривой неособые, т.е. производные
 одновременно в 0 не обращаются
одновременно в 0 не обращаются
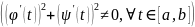 .
.
Эллипс, гипербола – гладкие кривые.
Старшие производные и дифференциалы функций.
Опр.
В
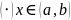 у функции
существует вторая производная
у функции
существует вторая производная
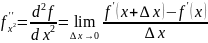 ,
если этот предел существует и конечен.
,
если этот предел существует и конечен.
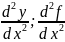 – обозначение
второй производной
– обозначение
второй производной
Если вторая производная существует в каждой точке интервала , то говорят, что функция дважды дифференцируема на множестве Х.
Если вторая производная определена на интервале, то первая производная и сама функция непрерывна на этом интервале.
Опр.
В
у функции
существует вторая производная
 ,
если этот предел существует и конечен.
,
если этот предел существует и конечен.
Опр.
Функция
принадлежит классу гладкости
 на Х,
если она имеет -ю производную, являющуюся
непрерывной функцией.
на Х,
если она имеет -ю производную, являющуюся
непрерывной функцией.
 – функция
n
раз непрерывно дифференцируема.
– функция
n
раз непрерывно дифференцируема.
|
|
|
|
Дифференциалы старшего порядка для функций одной переменной.
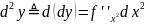 Второй
дифференциал сам является функцией
переменной х.
Второй
дифференциал сам является функцией
переменной х.
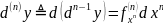 – корректно,
если функция n
раз
дифференцируема.
– корректно,
если функция n
раз
дифференцируема.
Свойства производной и дифференциала старшего порядка.
Теорема.
Если
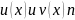 раз дифференцируемы на множестве Х,
тогда функции
раз дифференцируемы на множестве Х,
тогда функции
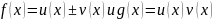 также являются
также являются
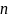 раз дифференцируемыми функциями, при
этом справедливы формулы:
раз дифференцируемыми функциями, при
этом справедливы формулы:

Доказательство последних двух методом математической индукции.
Производные и дифференциалы старших порядков для сложных функций.
Теорема. Если внутренняя функция n раз дифференцируема (т.е. имеет конечные n производных), и внешняя функция так же n раз дифференцируема, то и сложная функция n раз дифференцируема (т.е. имеет производные до n-го порядка по переменной x и дифференциалы n-го порядка).
В данном случае дифференциал dy константой не является, Это функция переменной х, а dx есть константа.
Второй дифференциал не является инвариантным при замене переменной.
Форма второго дифференциала и более старших инвариантна при линейной замене переменной.
Старшие производные параметрически заданных функций.