9. Системы линейных алгебраических уравнений. Теорема Кронекера-Капелли.

Система m линейных уравнений с n неизвестными (или, линейная система) в линейной алгебре — это система уравнений вида:

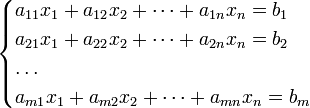
Теорема: Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы, причём система имеет единственное решение, если ранг равен числу неизвестных, и бесконечное множество решений, если ранг меньше числа неизвестных.   Доказательство.

            1) Если решение существует, то столбец свободных членов есть линейная комбинация столбцов матрицы А, а значит добавление этого столбца в матрицу, т.е. переход АА^* не изменяют ранга.

            2) Если RgA = RgA^*, то это означает, что они имеют один и тот же базисный минор. Столбец свободных членов – линейная комбинация столбцов базисного минора, те верна запись, приведенная выше.

10. Однородна система всегда совместна т.к. нулевой вектор является его решением , Если ранг однородной системы = числу неизвестных то система имеет нулевое решение . Если ранг однородной системы ˂ числе неизвестных , н , то существует (н-р)линейно независимых решений х1 ….хн этой системы и любое решение системы выражается через них : х=с1х1+..+сн-р хн-р

Векторы = х1…. хн-р образуют фундаментальную систему решений .

Общее решение неоднородной системы линейных уравнений равно сумме общего решения приведенной однородной системы и любого частного решения неоднородной системы.

11. Собственные значения

У матрицы A , размерностью (N×N) не может быть больше чем N собственных значений. Они удовлетворяют характеристическому уравнению  

det(A − λI) = 0, 

являющемуся алгебраическим уравнением N-го порядка. В частности, для матрицы 2×2 характеристическое уравнение имеет вид

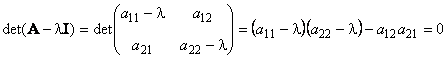
Собственные векторы

У матрицы A, размерностью (N×N) не может быть больше чем N собственных векторов, каждый из которых соответствует своему собственному значению. Для определения собственного вектора v_n нужно решить систему однородных уравнений 

(A − λ_nI) v_n = 0. 

Она имеет нетривиальное решение, поскольку det(A − λ_nI) = 0. 

Свойства :

• Линейная комбинация собственных векторов матрицы M, соответствующих одному и тому же собственному значению λ, также является собственным вектором M с собственным значением λ.

• Количество различных собственных значений не может превышать размер матрицы.

• Сумма размерностей собственных подпространств, соответствующих всем собственным значениям равна размерности матрицы (в случае рассмотрения комплексных чисел).

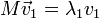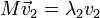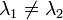• Собственные векторы, самосопряженного оператора А соответствующие различным собственным значениям ортогональны. Т. е. если , и , то

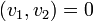
Для произвольной матрицы это не верно.

 

12. Определение: Множество L называется линейным (векторным) пространством, а его элементы называются векторами.  

Линейная зависимость и независимость векторов

     Система линейно зависима 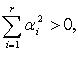что

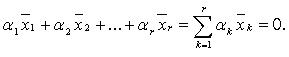
     Система линейно независима

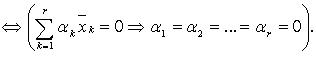
Свойства линейно зависимых и линейно независимых векторов

1. Если в систему векторов входит нулевой вектор, то она линейно зависима

.

2. Если в системе векторов имеется два равных вектора, то она линейно зависима.

3. Если в системе векторов имеется два пропорциональных вектора , то она линейно зависима.

4. Система из векторов линейно зависима тогда и только тогда, когда хотя бы один из векторов есть линейная комбинация остальных.

5. Любые векторы, входящие в линейно независимую систему, образуют линейно независимую подсистему.

6. Система векторов, содержащая линейно зависимую подсистему, линейно зависима.

7. Если система векторов линейно независима, а после присоединения к ней вектора оказывается линейно зависимой, то вектор можно разложить по векторам , и притом единственным образом, т.е. коэффициенты разложения находятся однозначно.

13. Определение 1. Базисом¹⁾ ненулевого векторного пространства над полем 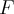называется система векторов, которая

1. порождает ,

2. линейно независима.

Теорема 1. Ненулевое векторное пространство всегда обладает базисом. Иными словами, является свободным -модулем.

Определение 2. Размерностью²⁾ ненулевого векторного пространства называется мощность его базиса. Для нулевого векторного пространства полагают, что его размерность равна нулю. Размерность векторного пространства над полем обозначается через .

Определение 3. Говорят, что пространство конечномерно³⁾, если или базис состоит из конечного числа векторов. В противном случае говорят, что бесконечномерно⁴⁾.

Определение 3. Пусть — базис , и . Скаляры называются координатами⁶⁾ вектора в данном базисе. п.2. Разложение вектора по базису.

Определение. Пусть  – произвольный вектор,  – произвольная система векторов. Если выполняется равенство

                   ,                       (1)

то говорят, что вектор  представлен в виде линейной комбинации данной системы векторов. Если данная система векторов  является базисом векторного пространства, то равенство (1) называется разложением вектора  по базису . Коэффициенты линейной комбинации  называются в этом случае координатами вектора  относительно базиса .

Теорема. (О разложении вектора по базису.)

Любой вектор векторного пространства можно разложить по его базису и притом единственным способом.

14. Определение: Множество L называется линейным (векторным) пространством, а его элементы называются векторами.  

Подпространство линейного пространства

     Множество называется подпространством линейного пространства V, если:

     1)

     2)

Определение. Линейной оболочкой L(х1, х2, х3, …, хk) векторов х1, х2, х3, и хk называется множество всех линейных комбинаций этих векторов. Про линейную оболочку можно сказать, что

- линейная оболочка является линейным подпространством;

– линейная оболочка является минимальным линейным подпространством, содержащим векторы х1, х2, х3, и хk.

15.

1