
- •Введение
- •Предмет теории вероятностей и математической статистики
- •Часть 1: Теория вероятностей
- •Глава 1: События и их вероятности
- •1. Понятие события
- •2. Элементарные события
- •3. Алгебра событий
- •4. Вероятность события
- •5. Свойства вероятности
- •6. Вероятностные схемы
- •Глава 2: Вероятности сложных событий
- •7. Условная вероятность. Независимые события
- •8. Вероятность произведения событий
- •9. Вероятность суммы событий
- •10. Формула полной вероятности. Формула Байеса
- •Глава 3: Системы независимых испытаний
- •11. Схема Бернулли
- •12. Наивероятнейшее число появления события
- •13. Приближения Лапласа
- •14. Приближение Пуассона
- •Глава 4: Цепи Маркова и случайные процессы
- •Глава 5: Случайные величины
- •Понятие случайной величины
- •Дискретные случайные величины
- •Непрерывные случайные величины
- •Параметры распределения случайных величин
- •Системы случайных величин
- •Глава 6: Основные виды распределений
- •Стандартные случайные величины
- •Равномерное распределение
- •Биномиальное распределение
- •Распределение Пуассона
- •Нормальное распределение
- •Глава 7: Закон больших чисел
- •Часть 2: математическая статистика
- •Глава8: Статистическая обработка данных
- •Понятие статистического исследования
- •Первичная обработка данных
- •Глава 9: Статистические оценки
- •Глава 10: Статистическая проверка гипотез
Дискретные случайные величины
Случайная величина называется дискретной, если она может принимать только конечный или счётный ряд значений.
Пример: число очков, выпавших на игральной кости.
Закон распределения дискретной случайной величины можно задать в виде ряда распределения.
Рядом распределения дискретной случайной величины называется таблица, ставящая в соответствие значениям случайной величины (записанным в возрастающем порядке), вероятности того, что случайная величина принимает эти значения:
xi |
x1 |
x2 |
… |
xn |
pi |
p1 |
p2 |
… |
pn |
Исходя из того, что случайная величина в результате испытания обязательно принимает одно из своих значений, и того, что случайная величина не может принять два значения одновременно, можно получить следующее свойство ряда распределения: сумма вероятностей, стоящих таблице, равна единице (даже если ряд значений счётен).
Графическое изображение ряда распределения называется полигоном.
Пример:
Непрерывные случайные величины
Случайная величина называется непрерывной, если она может принимать непрерывный ряд значений из некоторого отрезка (интервала).
Пример: дальность прыжка с места.
Закон распределения непрерывной случайной величины можно задать в форме плотности распределения.
Плотностью
распределения
непрерывной случайной величины называется
функция, являющаяся производной функции
распределения:
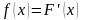 .
.
Плотность распределения можно определить как функцию, значение которой для некоторого аргумента равна пределу отношения вероятности попадания случайной величины в отрезок, содержащей аргумент, к длине этого отрезка, при стремлении последней к нулю.
Свойства плотности вероятности:
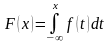 ;
;плотность вероятности является неотрицательной функцией;
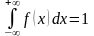 ;
;вероятность того, что непрерывная случайная величина примет какое-либо фиксированное значение равна нулю:
 ;
;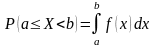 (при
этом знаки неравенств у промежутков
могут быть как строгими, так и нет).
(при
этом знаки неравенств у промежутков
могут быть как строгими, так и нет).
График плотности распределения называется кривой распределения. Кривая распределения, как и полигон, позволяет визуализировать распределение случайной величины. Площади фигур, ограниченных осью абсцисс, кривой распределения и вертикальными прямыми в границах интервала, численно равны вероятностям попадания случайной величины в соответствующий интервал.
Пример:
Параметры распределения случайных величин
Значение, которое принимает случайная величина, зависит от результата испытания. Гораздо более существенными характеристиками случайной величины, раскрывающими её свойства, являются параметры распределения. Параметры распределения не зависят от результатов отдельных испытаний и являются одной из реализаций закона больших чисел.
Положение распределения характеризуется математическим ожиданием случайной величины. Математическое ожидание является своего рода центром распределения.
Математическим ожиданием случайной величины Х называется среднее значение случайной величины в бесконечной серии испытаний (обозначение М(Х)).
Математическое ожидание является абстракцией понятия среднего значения случайной величины.
Формулы для вычисления математического ожидания:
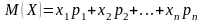 – для
дискретных случайных величин;
– для
дискретных случайных величин;
 – для
непрерывных случайных величин.
– для
непрерывных случайных величин.
Свойства математического ожидания:
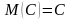 – математическое
ожидание постоянной величины равно
этой величине;
– математическое
ожидание постоянной величины равно
этой величине; – постоянную
величину можно выносить из-под знака
математического ожидания;
– постоянную
величину можно выносить из-под знака
математического ожидания;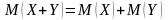 – математическое
ожидание суммы случайных величин равно
сумме их математических ожиданий;
– математическое
ожидание суммы случайных величин равно
сумме их математических ожиданий; – математическое
ожидание независимых
случайных величин равно произведению
математических ожиданий этих величин.
– математическое
ожидание независимых
случайных величин равно произведению
математических ожиданий этих величин.
Количественной характеристикой степени рассеяния значений случайной величины служит дисперсия случайной величины. Она показывает степень разброса значений случайной величины относительно её центра распределения.
Дисперсией
случайной величины Х
называется математическое ожидание
квадрата отклонения случайной величины
от её математического ожидания:
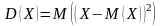 .
.
Формулы для вычисления дисперсии:
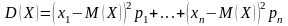 – для
дискретных случайных величин;
– для
дискретных случайных величин;
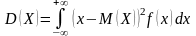 – для
непрерывных случайных величин.
– для
непрерывных случайных величин.
Дисперсию случайной величины удобней вычислять, используя не определение или указанные формулы, а одно из свойств дисперсии.
Свойства дисперсии:
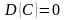 – дисперсия
постоянной величины равна нулю;
– дисперсия
постоянной величины равна нулю;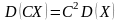 – постоянную
величину можно вынести из-под знака
дисперсии, возведя эту величину в
квадрат;
– постоянную
величину можно вынести из-под знака
дисперсии, возведя эту величину в
квадрат;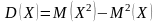 – дисперсия
случайной величины равна математическому
ожиданию квадрата случайной величины
без квадрата математического ожидания
этой величины;
– дисперсия
случайной величины равна математическому
ожиданию квадрата случайной величины
без квадрата математического ожидания
этой величины;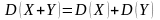 – дисперсия
суммы независимых
случайных величин равна сумме дисперсий
этих величин.
– дисперсия
суммы независимых
случайных величин равна сумме дисперсий
этих величин.
Существенным недостатком дисперсии (для практического использования) является следующий. Математическое ожидание случайной величины измеряется в тех же единицах, что и случайная величина, а дисперсия в соответствующих квадратных единицах. Для исключения этого недостатка в качестве характеристики рассеяния случайной величины вместо дисперсии используется среднеквадратичное (стандартное) отклонение.
Среднеквадратичным
отклонением случайной величины Х
называется квадратный корень из дисперсии
этой случайной величины:
 .
.
