3.Параметры выборки и распределения вероятностей

Эти параметры обычно разделяют на характеристики расположения и рассеяния. Наиболее распространенном характеристикой расположения является среднее значение. Если мы возьмем некоторое число n наблюденных значений переменной величины x, сложим их и разделим на число наблюдений, то получим среднее значение х как среднее арифметическое,

Основной мерой рассеяния выборочных значений является среднее квадратичное отклонение S, которое вычисляется по одной из двух следующих формул:

Вторая из них используется для достаточно больших n (n>10). она соответствует следующему простому правилу: ("квадрат среднеквадратичного есть среднее квадрата величины минус квадрат среднего").

Вернемся к примеру с n - бросаниями монеты. Если при i-ом бросании выпадает орел, то переменной будем присваивать значение 1, а в противоположном случае - 0. Число выпадении орла В соответствии с законом статнетической устойчивости, относительное значение частоты x/n будет колебаться около значения вероятности выпадения орла р=0,5. При этом, амплитуда отклонений относительной частоты x/n от значения р уменьшается в среднем. Таким образом, при достаточно больших n можно ожидать, что .

Далее мы можем рассмотреть более сложную ситуацию, когда проводится N серий с n- кратными бросаниями монеты (аналог N партий в каждой из которых делается выборка объема n). Тогда мы получим серию числа "успехов" . при этом . Действительно,

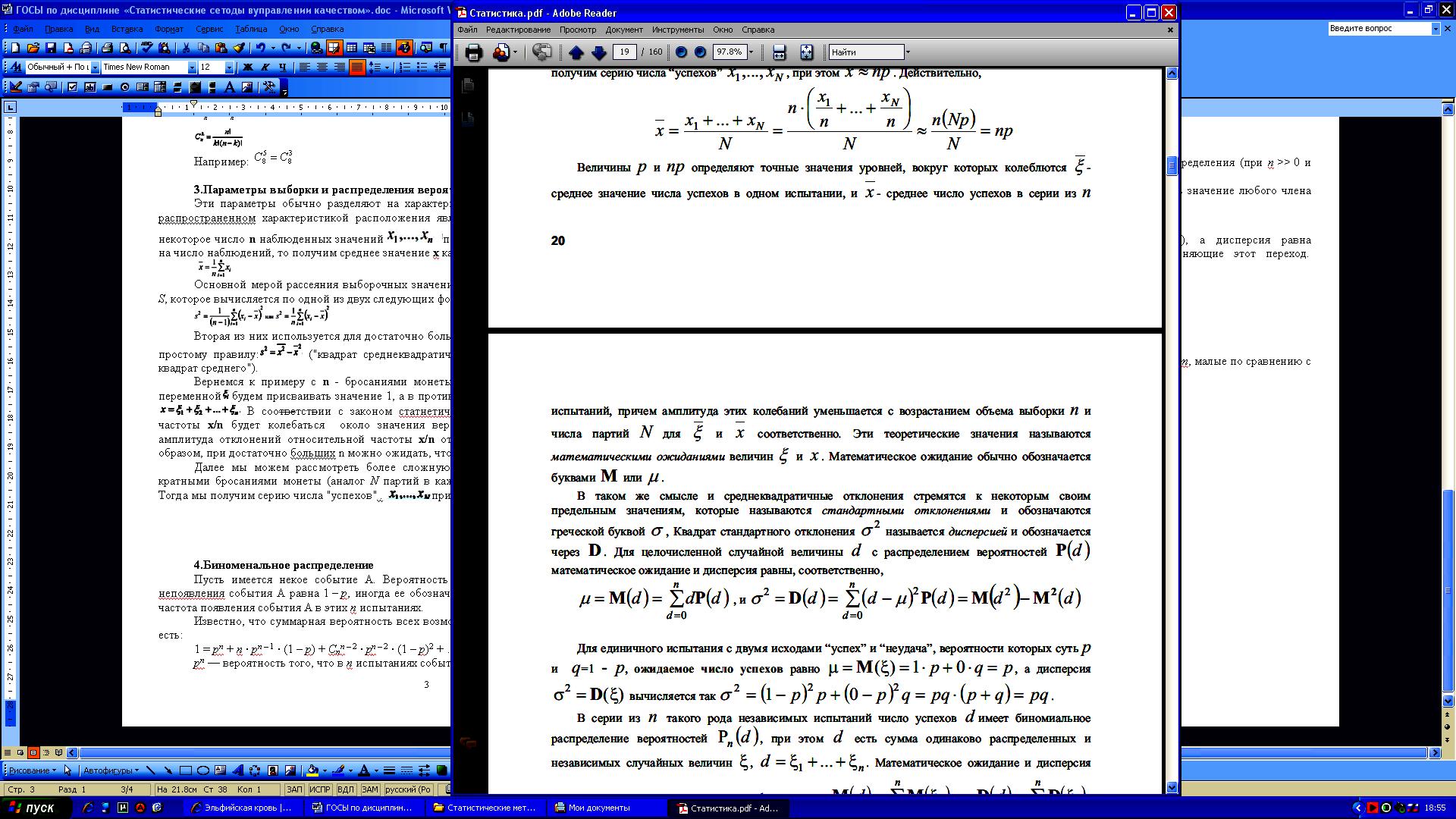
Величины p и np определяются точные значения уровней, вокруг которых колеблются -среднее значение числа успехов в одном испытании, и среднее число успехов в серии из n испытаний, причем амплитуда этих колебаний уменьшается с возрастанием объема выборки n и числа партий N для и cоответствешю. Эти теоретические значения называются математическими ожиданиями величин . Математическое ожидание обычно обозначается буквами М или

В таком же смысле в среднеквадратичные отклонения стремятся к некоторым своим предельным значениям, которые называются стандартными отклонениями и обозначаются

греческой буквой . Квадрат стандартного отклонения называется дисперсией и обозначается через D. Для целочисленной случайной величины d с распределением вероятностей Р(d) математическое ожидание и дисперсия равны, соответственно.

Для единичного испытания с двумя исходами "успех" и "неудача", вероятности которых суть р и ожидаемое число успехов равно , а дисперсия вычисляется так

В серии из n такого рода независимых испытании число успехов d имеет биномиальное распределение вероятностей , при этом d есть сумма одинаково распределенных и независимых случайных величин Математическое ожидание и дисперсия таких сумм выражаются простыми формулами,

Используя эти формулы и приведенные ваше результаты для единичного испытания, мы подучим следующие выражения для основных параметров биномиального распределения вероятностей:

Если все выборочные значения независимы и распределены одинаково, то математическое ожидание среднего совпадает с математическим ожиданием любого из слагаемых . поскольку их математические ожидания равны между собой, . Пусть есть константа (число), тогда для случайной величины , справедливы следующие равенства: . В силу последней формулы дисперсия среднего равна , то есть в N раз меньше дисперсии каждого отдельного слагаемого.

Соответственно, стандартное отклонение среднего , в раз меньше стандартного отклонения любого из слагаемых . Сказанное выше означает, что амплитуда случайных колебаний около числа с увеличением N уменьшается как . При больших N среднее можно использовать в качестве оценки математическою ожидания , и наоборот есть оценка X при больших N. Точно также СКО является при больших N оценкой стандартного отклонения (и наоборот).Рагмах R- что еще одна характеристика ряда выборочных значений. Размах равен разнице между наибольшим и наименьшим значениями в выборке