4.Биноменальное распределение

Пусть имеется некое событие A. Вероятность появления события A равна p, вероятность непоявления события A равна 1 – p, иногда ее обозначают как q. Пусть n — число испытаний, m — частота появления события A в этих n испытаниях.

Известно, что суммарная вероятность всех возможных комбинаций исходов равна единице, то есть:

1 = pⁿ + n · p^n – 1 · (1 – p) + C_n^n – 2 · p^n – 2 · (1 – p)² + … + C_n^m · p^m · (1 – p)^n – m + … + (1 – p)ⁿ.

pⁿ — вероятность того, что в n испытаниях событие A произойдет n раз;

n · p^n – 1 · (1 – p) — вероятность того, что в n испытаниях событие A произойдет (n – 1) раз и не произойдет 1 раз;

C_n^n – 2 · p^n – 2 · (1 – p)² — вероятность того, что в n испытаниях событие A произойдет (n – 2) раза и не произойдет 2 раза;

P_m = C_n^m · p^m · (1 – p)^n – m — вероятность того, что в n испытаниях событие A произойдет m раз и не произойдет (n – m) раз;

(1 – p)ⁿ — вероятность того, что в n испытаниях событие A не произойдет ни разу;

— число сочетаний из n по m.

Математическое ожидание M биномиального распределения равно:

M = n · p,

где n — число испытаний, p — вероятность появления события A.

Среднеквадратичное отклонение σ:

σ = sqrt(n · p · (1 – p)).

5. Распределение Пуассона.

Распределение Пуассона — это частный случай биномиального распределения (при n >> 0 и при p –> 0 (редкие события)).

Из математики известна формула, позволяющая примерно подсчитать значение любого члена биномиального распределения:

где a = n · p — параметр Пуассона (математическое ожидание), а дисперсия равна математическому ожиданию. Приведем математические выкладки, поясняющие этот переход. Биномиальный закон распределения

P_m = C_n^m · p^m · (1 – p)^n – m

может быть написан, если положить p = a/n, в виде

или

Так как p очень мало, то следует принимать во внимание только числа m, малые по сравнению с n. Произведение

весьма близко к единице. Это же относится к величине

Величина

очень близка к e^–a. Отсюда получаем формулу:

6. Нормальное распределение вероятности

Нормальное распределение выделяется своим фундаментальным значением среди остальных распределений. Ему подчиняются непрерывные случайные величины , значения которых зависит от большого числа случайных воздействий. Это в равной степени могут быть случайные ошибки эксперимента и множество случайных воздействий на технологический процесс.

Важным для практики свойством нормального закона является то, что он является хорошей аппроксимацией биномиального и пуассоновского распределений при достаточно больших и .

Распределение вероятностей для среднего значения

выборки обычно близко к нормальному закону даже, если отдельные выборочные значения распределены существенно иным образом.

Нормальной плотностью вероятности называется плотность, определяемая равенством

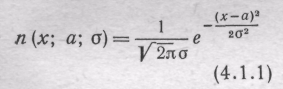
для любого значения , где —произвольные числа (параметры распределения), причем положительно.

Рис. 2.6

Нормальная плотность вероятности называется также дифференциальной функцией нормального распределения. График дифференциальной функции нормального распределения показан на рис. 2.6.

Интегральная функция нормального распределения определяется в виде

полная площадь под всей кривой выразится интегралом

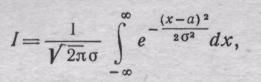
который путем замены переменного на _, откуда и _, преобразуется в интеграл

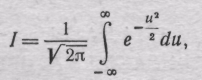
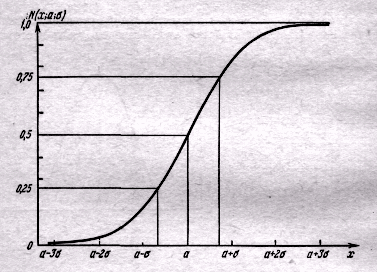
График интегральной функции распределения показан на рис. 2.7.

Из рисунка видно, что плотность нормального распределения симметрична относительно ординаты, отвечающей значению x=a

Это значение является поэтому центром группирования (математическим ожиданием) распределения.

Ч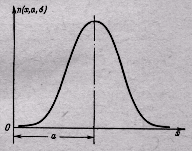 аще всего, однако, рассматривая величину, подчиненную нормальному закону переходят к нормированному распределению.

Нормирование распределения, вообще говоря, заключается в переходе от величины к вспомогательной линейной функции

……

Рис. 2.7

для которой

При нормальном распределении будем иметь:

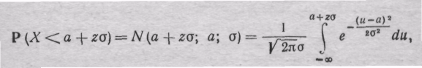
или

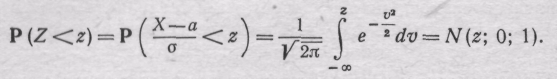
После дифференцирования получим

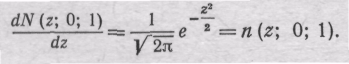
Все вопросы, связанные с нормальным распределением величины решают, переходя к вспомогательной величине _, т. е. нормируя это распределение.

Нормирование распределения, как нетрудно понять, ведет просто к перенесению начала координат в центр группирования, т. е. к «центрированию», и к выражению абсциссы в долях которое, как мы дальше увидим, представляет среднеквадратическое отклонение величины т. е.