11.Сетевой график.Понятие критического пути.Задача его поиска. 12.Основные понятия теории графов.Матрицы смежности,инцидентности,достижимости и связанности. Матрица достижимости орграфа — это матрица, содержащая информацию о существовании путей между вершинами в орграфе.
Матрица инцидентности графа — это матрица, значения элементов которой характеризуется инцидентностью соответствующих вершин графа (по вертикали) и его рёбер (по горизонтали). Для неориентированного графа элемент принимает значение 1, если соответствующие ему вершина и ребро инцидентны. Для ориентированного графа элемент принимает значение 1, если инцидентная вершина является началом ребра, значение -1, если инцидентная вершина является концом ребра; в остальных случаях (в том числе и для петель) значению элемента присваивается 0.
Матрица смежности графа — это матрица, значения элементов которой характеризуются смежностью вершин графа. При этом значению элемента матрицы присваивается количество рёбер, которые соединяют соответствующие вершины (то есть которые инцидентны обоим вершинам). Петля считается сразу двумя соединениями для вершины, то есть к значению элемента матрицы в таком случае следует прибавлять 2.
Минимальный каркас графа — ациклическое множество рёбер в связном, взвешенном и неориентированном графе, соединяющих между собой все вершины данного графа, при этом сумма весов всех рёбер в нем минимальна.
Множество смежности вершины v — множество вершин, смежных с вершиной v. Обозначается Γ + (v)
Мультиграф — граф, в котором существует пара вершин, которая соединена более чем одним ребром (ненаправленным), либо более чем двумя дугами противоположных направлений.
13.Алгоритм поиска кратчайшего пути между двумя вершинами Дейкстры . Алгоритм поиска кратчайшего пути
Результатом алгоритма поиска кратчайшего пути является последовательность ребер, соединяющая заданные две вершины и имеющая наименьшую длину среди всех таких последовательностей. На первый взгляд кажется, что мы можем воспользоваться алгоритмом построения МОД, чтобы отбросить лишние ребра, а затем взять путь, соединяющий заданные вершины в построенном остовном дереве. К сожалению, такие действия не всегда приводят к нужному результату. Напомним, что алгоритм построения МОД нацелен на поиск дерева с минимальным суммарным весом ребер. Рассмотрим, например, "циклический" граф, то есть такой граф, в котором первая вершина соединена со второй, вторая - с третьей, и так далее, а последняя вершина в свою очередь соединена с первой. Такой граф представляет собой просто кольцо, каждая вершина в котором соединена с двумя другими. Пример такого графа с шестью вершинами приведен на рис. 1 (а).
Обратите внимание на то, что вес каждого ребра равен 1 за исключением ребра, соединяющего вершины A и B, вес которого равен 2. Алгоритм построения минимального остовного дерева выберет все ребра веса 1, отбросив единственное ребро веса 2. Это означает, однако, что путь от A к B в минимальном остовном дереве должен проходить через все остальные вершины, а его длина равна 5 (рис. 1 (б)). Ясно, что он не является кратчайшим, поскольку в исходном графе вершины A и B соединены ребром длины 2.
15.Метод ветвей и границ (Задача коммивояжера). идея метода может быть описана на примере поиска минимума и максимума функции f(x) на множестве допустимых значений x. Функция f и x могут быть произвольной природы. Для метода ветвей и границ необходимы две процедуры: ветвление и нахождение оценок (границ).
Процедура ветвления состоит в разбиении области допустимых решений на подобласти меньших размеров. Процедуру можно рекурсивно применять к подобластям. Полученные подобласти образуют дерево, называемое деревом поиска или деревом ветвей и границ. Узлами этого дерева являются построенные подобласти.
Процедура нахождения оценок заключается в поиске верхних и нижних границ для оптимального значения на подобласти допустимых решений.
В основе метода ветвей и границ лежит следующая идея (для задачи минимизации): если нижняя граница для подобласти A дерева поиска больше, чем верхняя граница какой-либо ранее просмотренной подобласти B, то A может быть исключена из дальнейшего рассмотрения (правило отсева). Обычно, минимальную из полученных верхних оценок записывают в глобальную переменную m; любой узел дерева поиска, нижняя граница которого больше значения m, может быть исключен из дальнейшего рассмотрения.
Если нижняя граница для узла дерева совпадает с верхней границей, то это значение является минимумом функции и достигается на соответствующей подобласти.
16.Задача о распределение потоков в сетях.теорема Форда-Фалкерсона.
Форда-Фалкерсона следующим образом. Будем доказывать для сети G(V,E) с потоком f равносильность сразу трёх следующих фактов:
1° Поток f - максимальный
2° Пропускная способность минимального разреза равна величине потока f
3° В графе G нет дополняющего пути
1° → 3°. Предположив обратное, получим противоречие, описанное в информации по дополняющем пути в транспортном графе.
3° → 2°. Очевидно, что величина потока f не превышает пропускной способности минимального разреза (S,T). Пусть c(S,T) > f. Тогда рассмотрим разрез, где во множествеS будут все вершины, кроме t. Тогда его пропускная способность не меньше пропускной способности минимального разреза, что, в свою очередь, больше величины потока f. Значит, существует направление (u,t) из S в T, что f(u,t) < c(u,t). Теперь возьмём все такие u и перенесём их в T. Рассмотрев получившийся разрез, заметим, что его пропускная способность тоже меньше величины потока. Снова увеличиваем множество T и делаем так до тех пор, пока в множестве S не останется только вершина s. Она же будет первой вершиной в пути, который мы создаём. Теперь смотрим какую пару мы выбрали прошлым ходом. Пусть это пара (s,u). Тогда к пути добавляем вершину u. Далее смотрим в паре с какой вершиной была на первом месте вершина u. Пусть это (u,v). Тогда далее к пути добавляем вершину v. Делаем так до тех пор, пока не дойдём до вершины t. Однако по построению этот путь является остаточным, что противоречит предположению.
2° → 1°. Как уже говорилось, очевидно, что величина любого потока не превышает пропускной способности минимального разреза, а величина нашего потока f - равна. Тогда величина потока f не меньше величины любого другого потока в нашей сети, т.е. поток f - максимальный.
Это доказательство хорошо тем, что не использует сложный алгоритм нахождения максимального потока в произвольной транспортной сети.
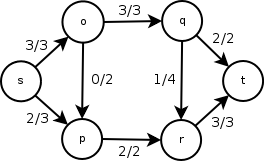
Сеть с 3-мя минимальными разрезами
Справа дана сеть с 6-ю вершинами V = {s,o,p,q,r,t}, и суммарный поток от истока s к стоку t равен 5. Этот поток является максимальным для данной сети.
В данной сети возможны 3 минимальных разреза:
-
Cut
Capacity
S = {s,p},T = {o,q,r,t}
c(s,o) + c(p,r) = 3 + 2 = 5
S = {s,o,p},T = {q,r,t}
c(o,q) + c(p,r) = 3 + 2 = 5
S = {s,o,p,q,r},T = {t}
c(q,t) + c(r,t) = 2 + 3 = 5
18.метод нахождения минимального разреза и максимального потока методом Форда-Фалкерсона. Пусть имеется некоторое сечение между вершинами t и s. Тогда величиной сечения называется сумма пропускных способностей ребер, входящих в это сечение. Сечение называется минимальным (максимальным), если его величина минимальна (максимальна).
Теорема Форда – Фалкерсона (1955). Максимальный поток между вершинами t и s равен величине минимального сечения между этими вершинами.
Доказательство этой теоремы является конструктивным (т. е. показывает, как найти нужный максимальный поток), поэтому приводится ниже.
Докажем сначала, что любой поток между вершинами t и s меньше или равен величине любого сечения. Пусть дан некоторый поток и некоторое сечение. Величина данного потока складывается из величин “грузов”, перевозимых по всем возможным путям из вершины t в s. Каждый такой путь обязан иметь общее ребро с данным сечением. Так как по каждому ребру сечения суммарно нельзя перевести “груза” больше, чем его пропускная способность, поэтому сумма всех грузов меньше или равна, сумме всех пропускных способностей ребер данного сечения. Утверждение доказано.
Отсюда следует, что любой поток меньше или равен величине минимального сечения, а значит и максимальный поток меньше или равен величине минимального сечения.
Докажем теперь обратное неравенство. Пусть имеется некоторый поток cij (какой-то поток всегда существует, например, нулевой, когда все cij = 0). Будем помечать вершины графа, причем считаем, что все помеченные вершины образуют множество Y. Пометки вершин производятся от источника. Каждая пометка вершины (если эта вершина может быть помечена) состоит из двух чисел: первое – это “+” или “–” номер вершины (из Y), c которой связана новая помечаемая вершина, и второе – (обязательно должно быть положительным) – это фактически та добавка к потоку, которая может быть дополнительно “довезена” в эту вершину из источника по сравнению с исходным потоком.
11Сетевой график.Понятие критического пути.Задача его поиска
\ график, расписание последовательности выполнения и взаимосвязи работ, создаваемый для получения запланированного результата в намеченные сроки. Г.с. классифицируются: по числу целей - одноцелевые и многоцелевые; по видам ресурсов - временные, стоимостные; по степени охвата объектов - объектные и комплексные. Г.с. с наибольшей суммарной продолжительностью, длина которого определяет продолжительность выполнения всего комплекса работ для достижения поставленной цели, называется критическим путем.
Критического Пути
метод принятия решений, который основывается на предположении, что планируемый процесс займет максимально возможный промежуток времени, т.е. критический путь в сетевом графике.