Дифференциальные уравнения

1. Понятие о дифференциальном уравнении. Некоторые задачи, приводящие к дифференциальным уравнениям.

В тех случаях, когда научную или техническую проблему можно сформулировать более вероятно, что задача сведется к одному или нескольким дифференциальным уравнениям. Это всегда имеет место для широкого класса проблем, связанных с силами и движением. Например, нахождение траектории искусственного спутника, траектории электрона в синхрофазотроне, изучение закона движения самолета или локомотива.

В электронике, радиотехнике, электротехнике, гидро -аэродинамике, теплотехнике, физике, химии, биологии и многих других областях науки техники большое количество задач сводится к дифференциальным уравнениям.

Пусть функция y=f(x) отражает количественную сторону некоторого явления. Часто, рассматривая это явление, мы не можем непосредственно установить характер зависимости y от x, а можем установить зависимость между величинами х , y и производными от y по x: y^/, y^//,…,y⁽ⁿ⁾ , то есть написать дифференциальное уравнение.

Пример: с некоторой высоты сброшено тело, масса которого m. Требуется установить по какому закону будет изменяться скорость v падения этого тела, если на него, кроме силы тяжести, действует тормозящая сила сопротивления воздуха, пропорциональная скорости ( с коэффициентом пропорциональности к), то есть требуется найти v=f(t).

Решение. По второму закону Ньютона

m

-есть ускорение движущегося тела (производная скорости по времени), а F-сила, действующая на тело в направлении движения. Эта сила складывается из двух: силы тяжести mg и силы сопротивления воздуха -kv (знак «-», так как она направлена в сторону противоположную направлению скорости). Итак,

m

Мы получили соотношение, связывающее неизвестную функцию v и её производную , то есть дифференциальное уравнение относительно неизвестной функции v. (Это уравнение движения некоторых типов парашютов).

Определение. Дифференциальным уравнением называется уравнение, связывающее независимую переменную х, искомую функцию y и её производные y^/, y^//,…,y⁽ⁿ⁾.

Обозначают так:

F(x,y, y^/, y^//,…,y⁽ⁿ⁾)=0

или

F(x,y, , ,…, )=0

Если искомая функция у=f(x) есть функция одной независимой переменной, то дифференциальное уравнение называется обыкновенным.

Определение. Порядком дифференциального уравнения называется порядок наивысшей производной, входящей в уравнение.

Например, уравнения:

y^/=у²+sinx есть дифференциальное уравнение первого порядка,

y^//+ln(x+y+1)=0 есть дифференциальное уравнение второго порядка.

Определение. Решением дифференциального уравнения называется всякая функция у=f(x), которая, будучи подставлена в уравнение, обращает его в тождество.

2. Дифференциальные уравнения первого порядка

Дифференциальное уравнение первого порядка имеет вид:

F(x,y, y^/)=0 (1)

или

y^/=f(x,y)=0 (1^/)

то есть уравнение разрешено относительно производной.

Для такого уравнения справедлива теорема, которая называется теоремой о существовании и единственности решения дифференциального уравнения.

Теорема: если в уравнение

y′=f(x, y)

функция f(x, y) и ее частная производная _{по y непрерывны в некоторой области Д на плоскости Oxy, содержащий некоторую точку (x0,y0), то существует единственное решение этого уравнения:}

_y=φ(x),

_{удовлетворяющее условию y=y0 при x=x0 .}

_{Теорему примем без доказательства.}

_{Геометрически это означает, что существует и притом единственная функция y=φ(x), график которой проходит через точку (x0,y0).}

_{Из теоремы вытекает, что уравнение (1′) может иметь решение, график которого проходит через точку (x0,y1); другое решение, график которого проходит через точку (x0,y2) и т.д.То есть уравнение имеет бесконечное число различных решений.}

_{Условие, что при x=x0 ,y=y0 называется начальным условием и обозначают :}

₍₂₎

_{Задача отыскания решения дифференциального уравнения (1′), удовлетворяющего начальным условиям (2), называется задачей Коши.}

_{Определение. Общим решением дифференциального уравнения (1) называется функция y=φ(x,C),где С- произвольная постоянная и удовлетворяет следующим условиям:}

1. _{При любом С удовлетворяет дифференциальному уравнению.}

2. _{Какого бы ни было начальное условие , можно найти такое значение С=С0, что y=φ(x,C0) удовлетворяет данному начальному условию.}

_{В процессе решения уравнения общее решение получают в виде:}

_Ф(x,y,C)=0.

_{Определение. Частным решением дифференциального уравнения (1) называется функция y=φ(x,C0), которая получается из общего решения y=φ(x,C) и С=С0 определяют исходя из начальных условий (2).}

_{Процесс отыскания решений дифференциального уравнения называется интегрированием этого уравнения.}

3. _{МЕТОДЫ ИНТЕГРИРОВАНИЯ ПРОСТЕЙШИХ ТИПОВ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ПЕРВОГО ПОРЯДКА.}

   1. _{УРАВНЕНИЯ С РАЗДЕЛЯЮЩИМИСЯ ПЕРЕМЕННЫМИ.}

_{Рассмотрим дифференциальное уравнение вида:}

₍₁₎

_{где правая часть уравнения представляет произведение функции, зависящий только от x, на функцию, зависящий только от y.}

_{Предполагая, что f2(y)≠0,запишем уравнение (1) в виде:}

_(1′)

_{Равенство (1′) можно рассматривать как равенство двух дифференциалов, а неопределенные интегралы от них будут отличаться на постоянную величину, то есть:}

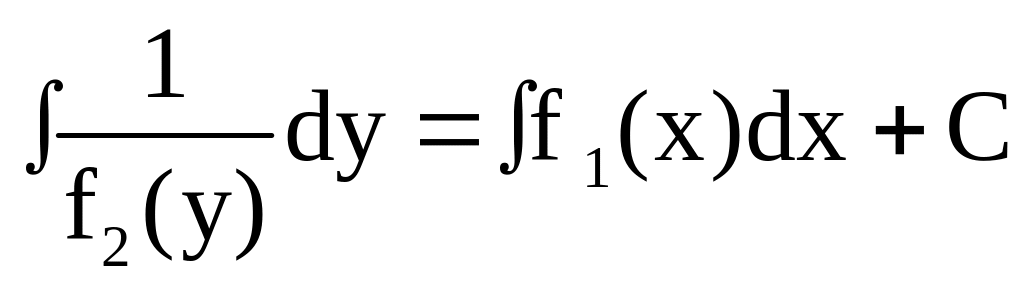
_{Последнее равенство есть решение дифференциального уравнения (1).}

_{Итак, дифференциальное уравнение вида}

_{M(x)dx+N(y)dy=0 (2)}

_{Называют уравнением с разделенными переменными.}

_{Его решением будет:}

_{Дифференциальное уравнение вида:}

_{M1(x)· N1(y)dx+ M2(x)· N2(y)dy=0 (3)}

_{Называют уравнением с разделяющимися переменными.}

_{Его легко привести к виду уравнения (2). Для этого разделим обе части уравнения на N1(y)· M2(x)}

_{Получим}

_{Пример. Решить уравнение}

_x(1-y²_)dx+y(1-x²_)dy=0

_{Уравнение с разделяющимися переменными. Разделим обе части уравнения на}

_(1-y²_{) ·(1-x}²₎

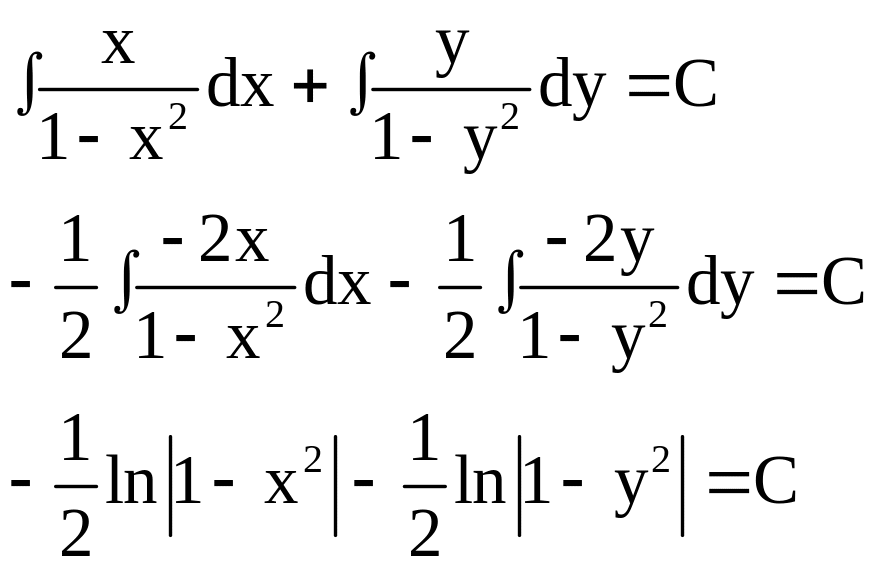
Умножим на (-2)

2С-const, ln C-const

_(1-y²_{) ·(1-x}²_{)=C- общее решение.}

_{Задача. Установлено, что скорость распада радия прямо пропорционально его количеству в каждый данный момент. Определить закон изменения массы радия в зависимости от времени, если при t=0 масса радия была m0.}

_{Решение. Пусть в момент времени t масса была m, в момент t+∆t масса m+∆m.}

Скорость распада радия в момент t

_{По условию задачи}

_{где k- коэффициент пропорциональности (k>0). Знак минус стоит потому ,что с увеличением времени масса радия убывает, следовательно}

Получим уравнение с разделяющимися переменными

Так как при t=0 m=m₀ ( начальные условия) определим значения постоянной С:

Получим Значение k определяется опытным путем.

3.2 ОДНОРОДНЫЕ УРУВНЕНИЯ.

Определение. Функция f(x,y) называется однородной функцией n-го измерения относительно переменных x и y, если при любом t справедливо тождество

f(tx,ty)=tⁿf(x,y)

Примеры.

1.f(x,y)=

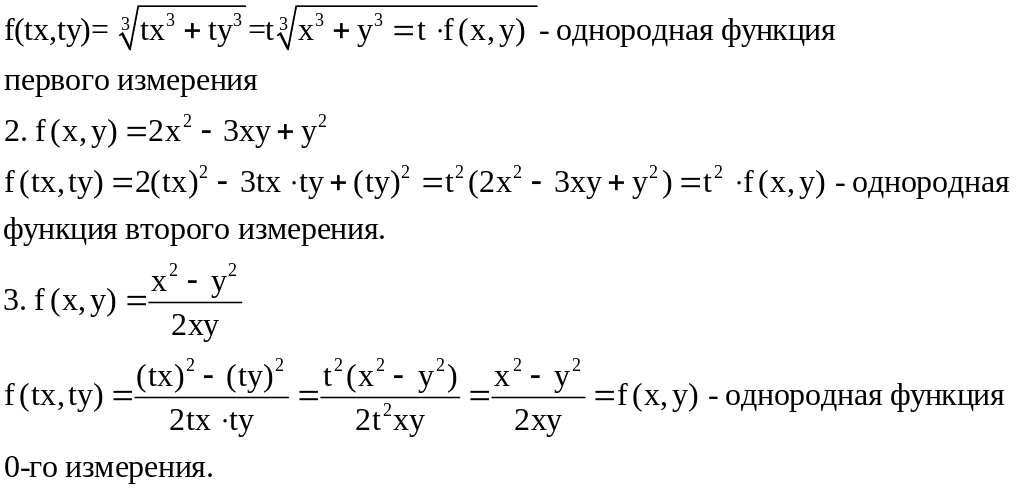
Определение. Дифференциальное уравнение первого порядка

y′=f(x, y) (1)

называется однородным относительно x и y, если функция f(x, y) есть однородная функция нулевого измерения относительно x и y.

Однородную функцию нулевого измерения всегда можно привести к ф-ии отношения переменных.

Действительно, т.к.

Пусть , то

Ур-ие (1) принимает вид (1’)

Сделаем подстановку

или ,

Тогда или

Подставим в ур-ие (1’), получим

Это ур-ие с разделяющимися переменными:

или

откуда

Интегрируя, найдем

Пример. Решить ур-ие

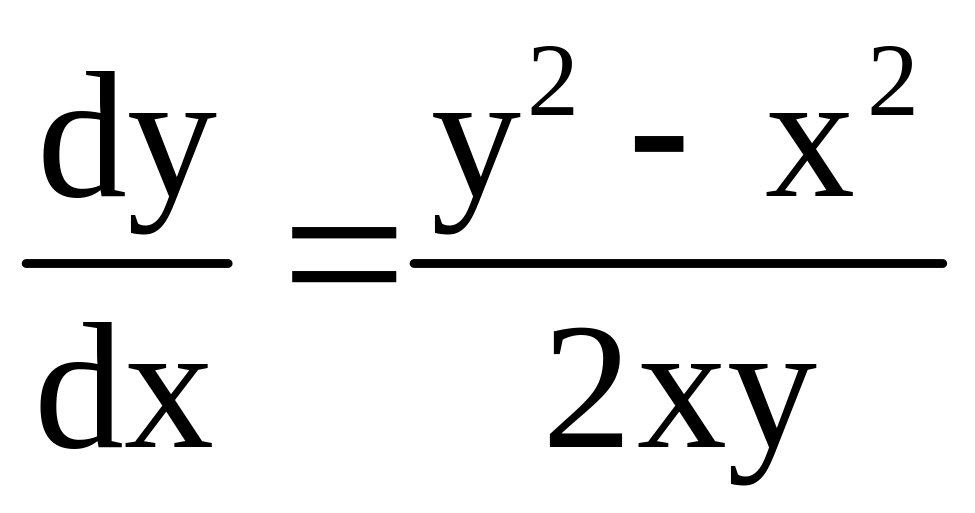разделим и числитель и знаменатель

правой части на

Общее решение

Замечание 1 Дифф-ое ур-ие вида

будет однородным только в том случае, если ф-ии и есть однородные ф-ии одного и того же измерения, т.е. –есть однородная ф-ия, нулевого измерения.

Замечание 2 Дифференциальное ур-ие вида называют однородным дифф-ым ур-ием первого порядка.