3.3. Уравнения, приводящиеся к однородным.

К однородным ур-ям приводятся ур-ия вида 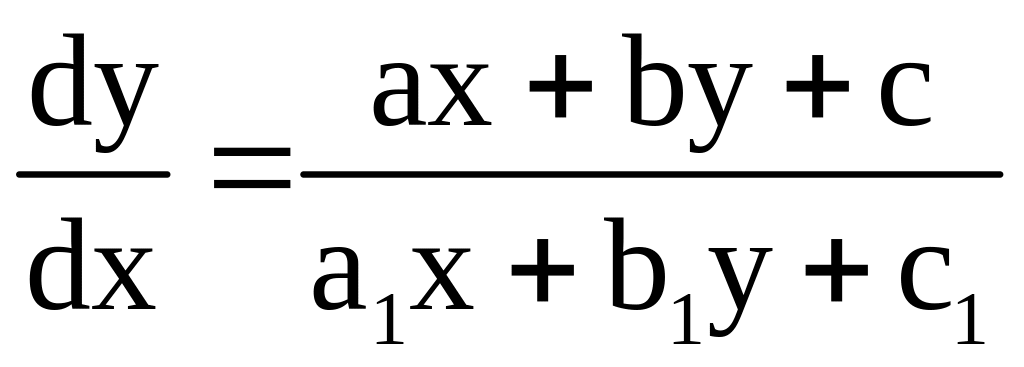(1)

где , - хотя бы одно из них отлично от нуля.

Пусть (2) тогда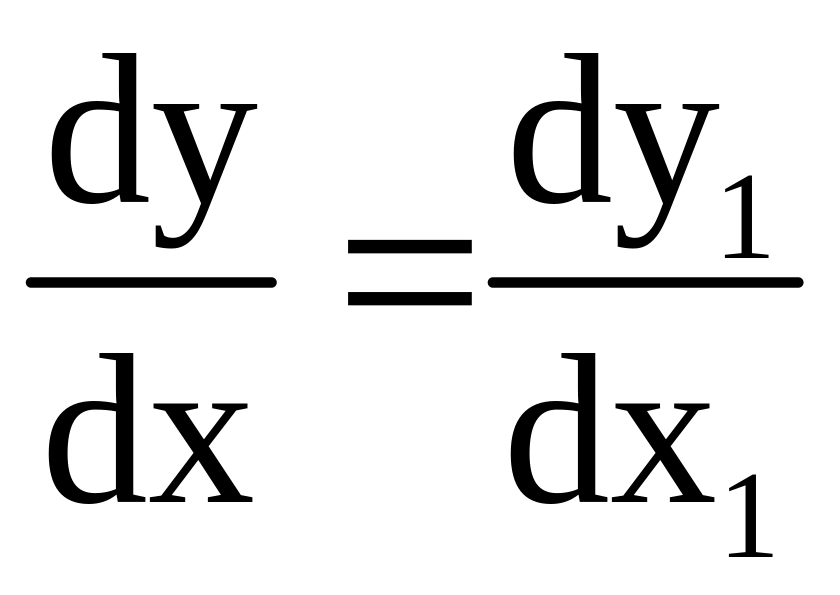

Подставим в ур-ие (1)

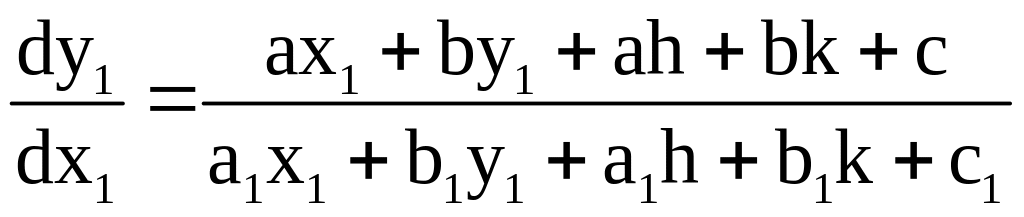(3)

Подберем и так, чтобы

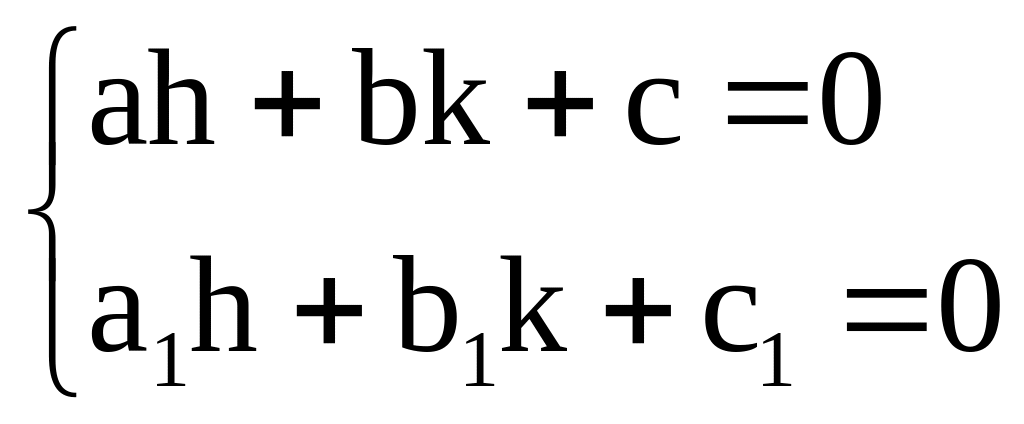(4)

Тогда ур-ие (3) примет вид

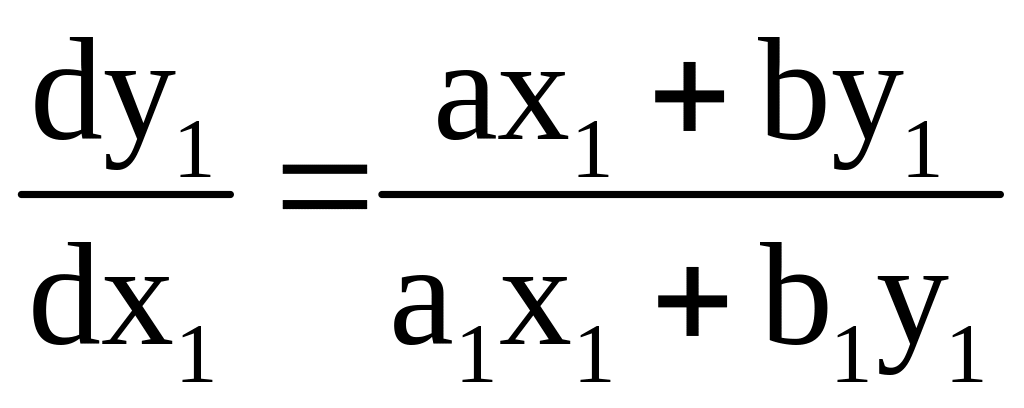
Это однородное ур-ие. Решив его и возвращаясь к переменным и по формулам (2) получим решение ур-ия (1).

Система (4) не имеет решения, если

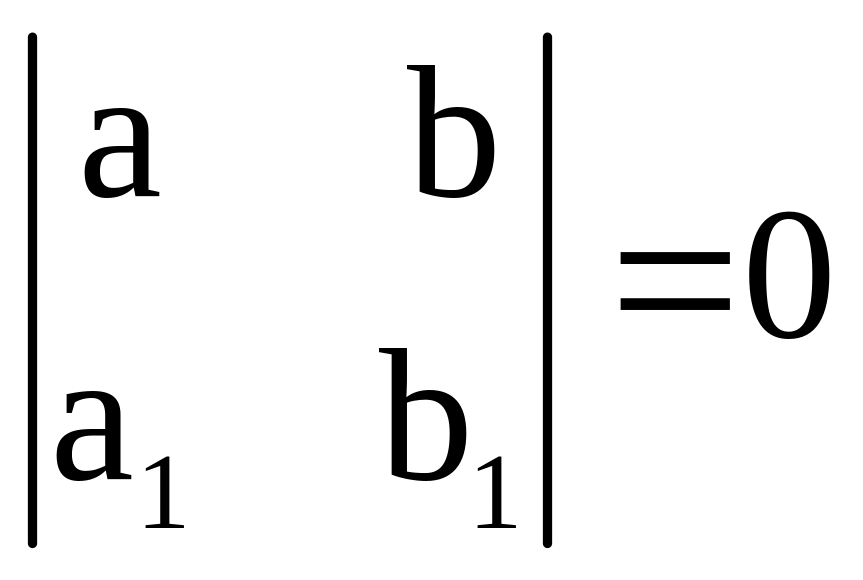
т.е. или

В этом случае обозначим

откуда , и ур-ие (1) примет вид

(5)

Тогда примем подстановку (6)

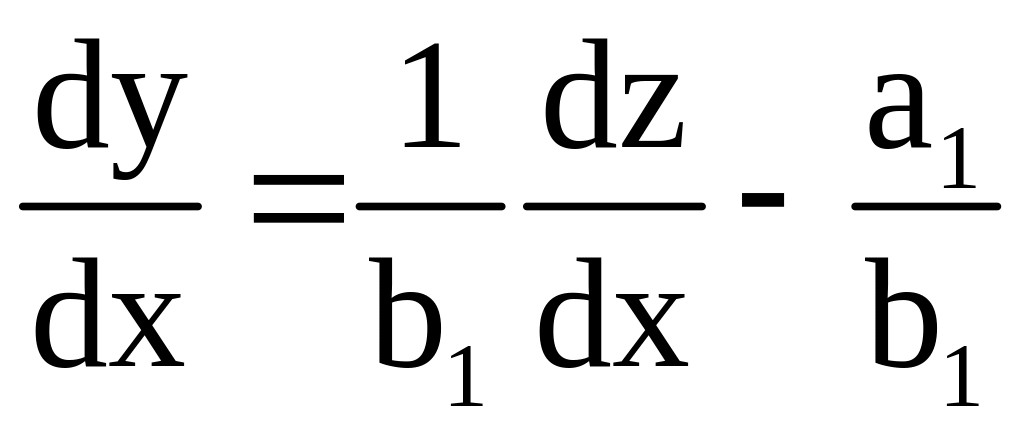(7)

Подставляя выражения (6) и (7) в ур-ие (5) получим

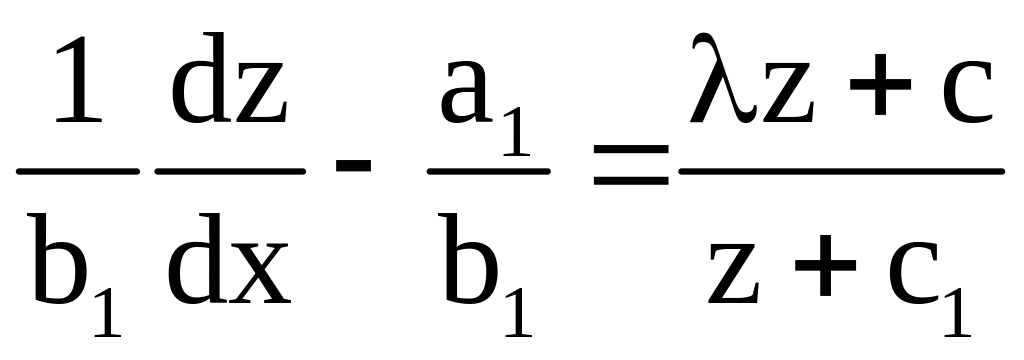
а это есть ур-ие с разделяющимися переменными.

Примеры.

1)

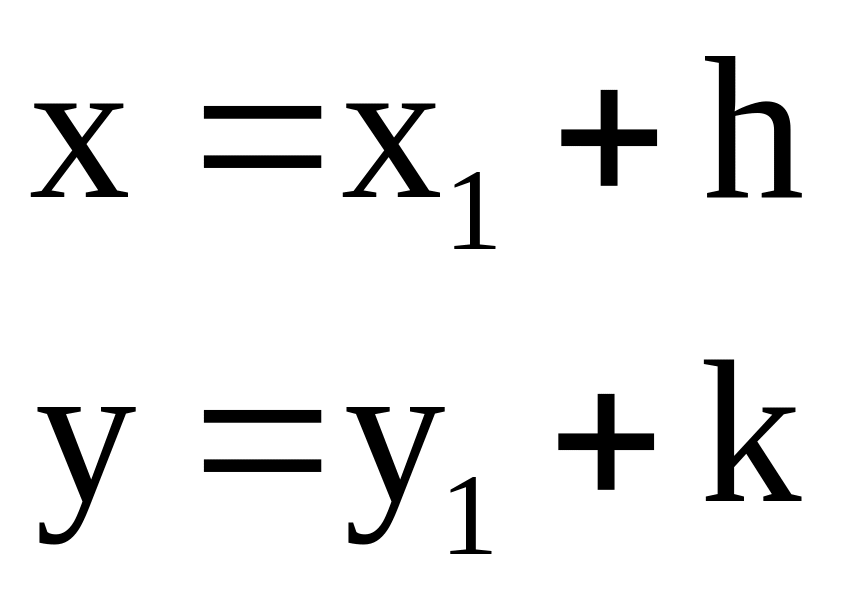
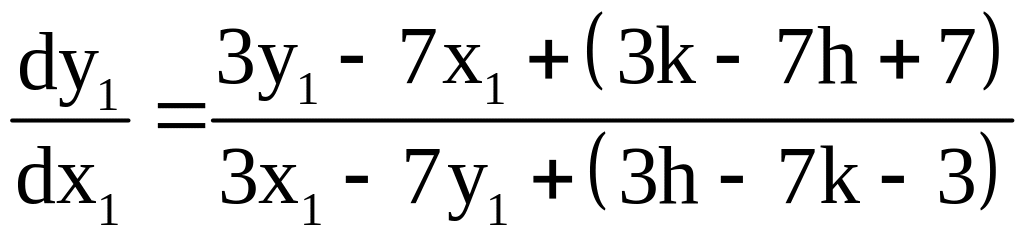
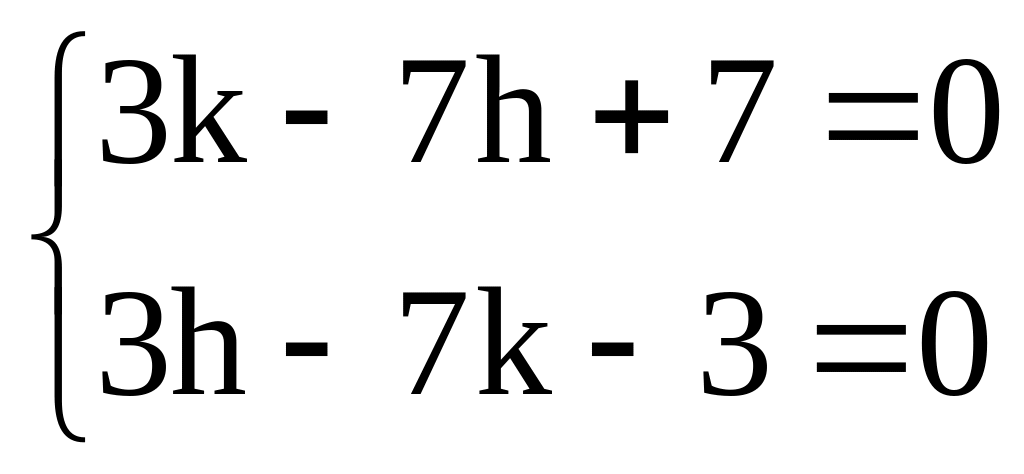
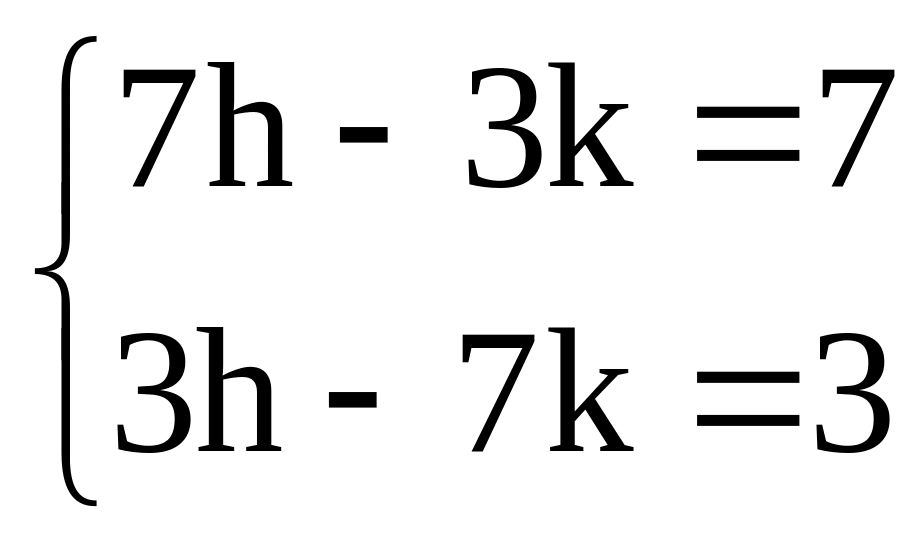
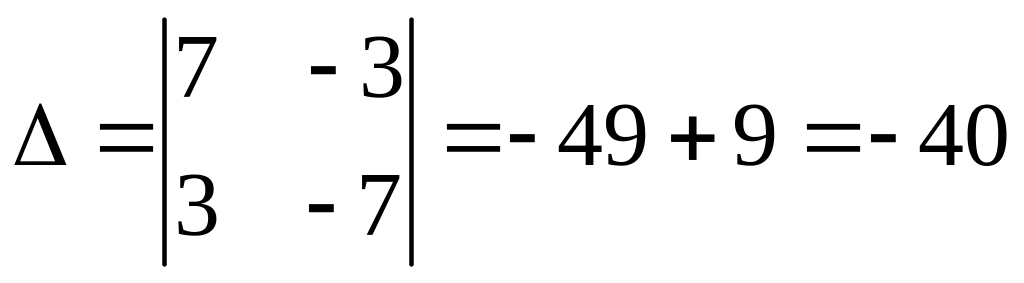
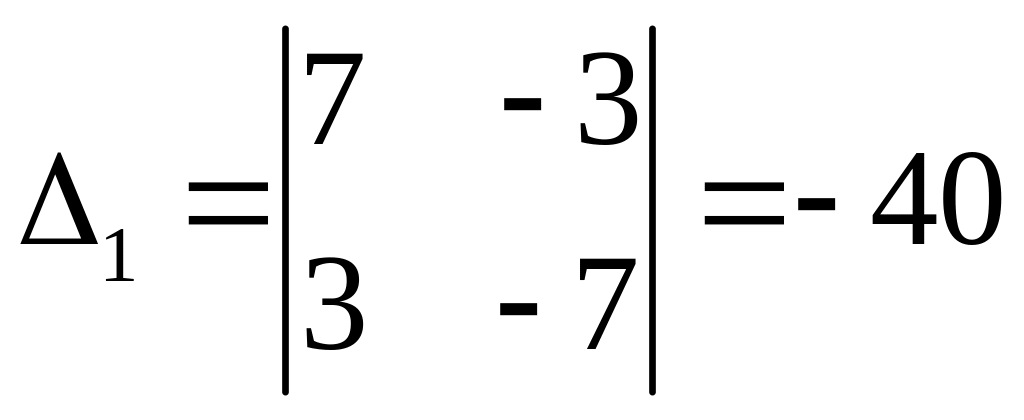
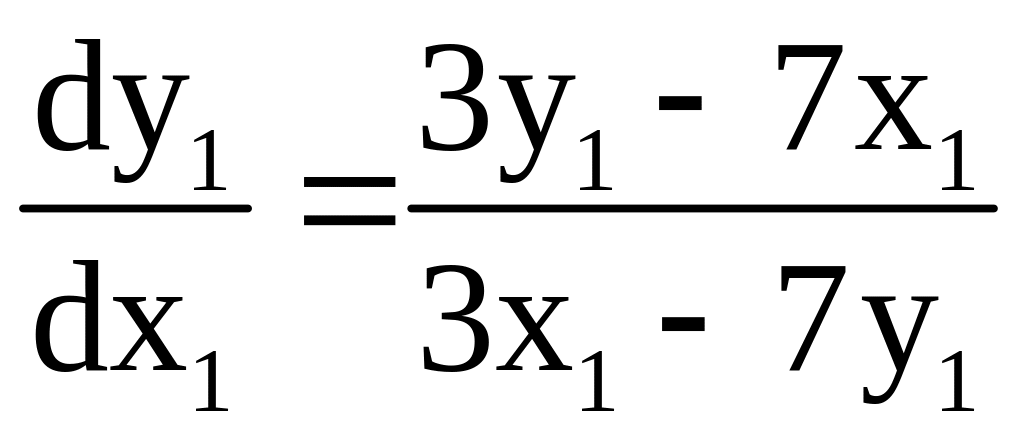
Ур-ие однородное

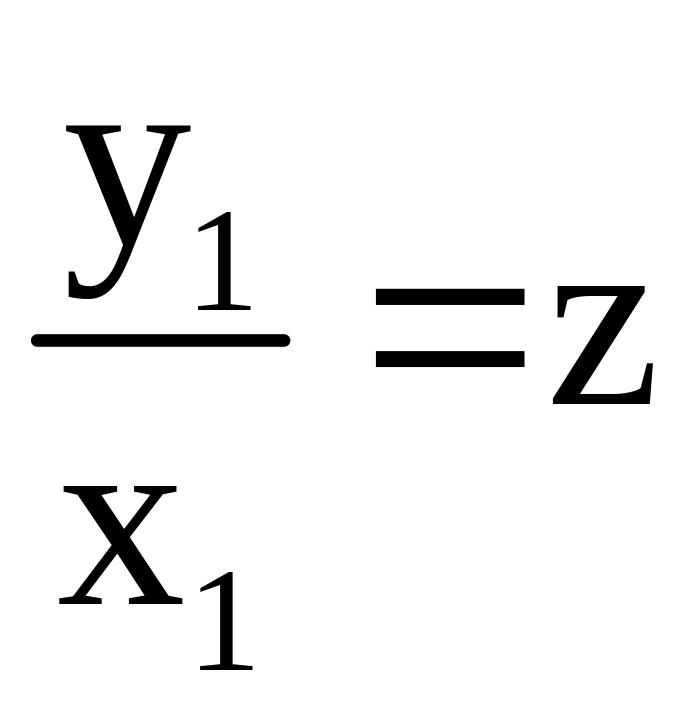
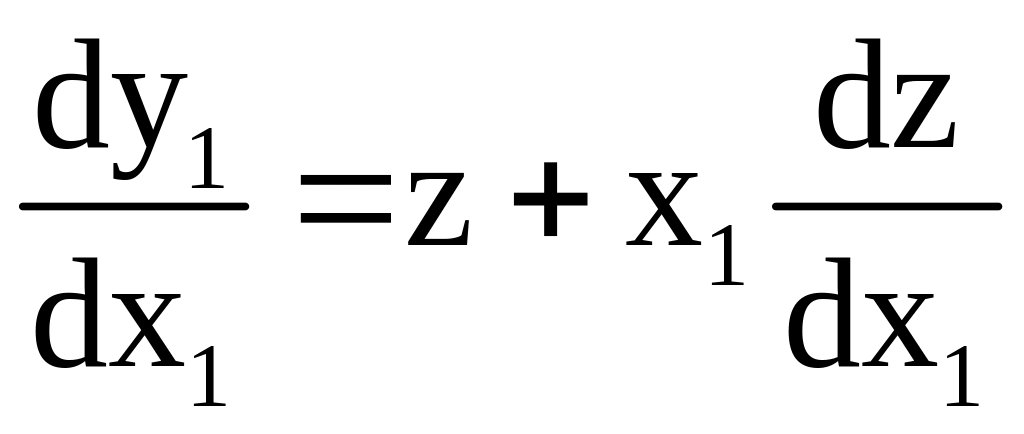
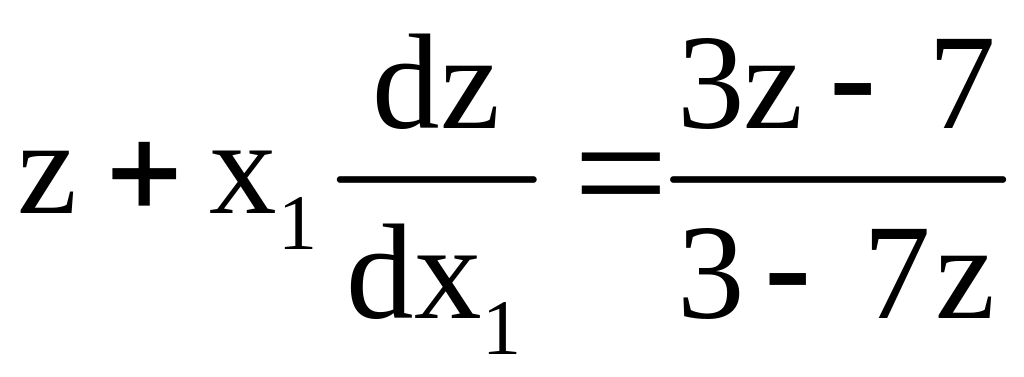
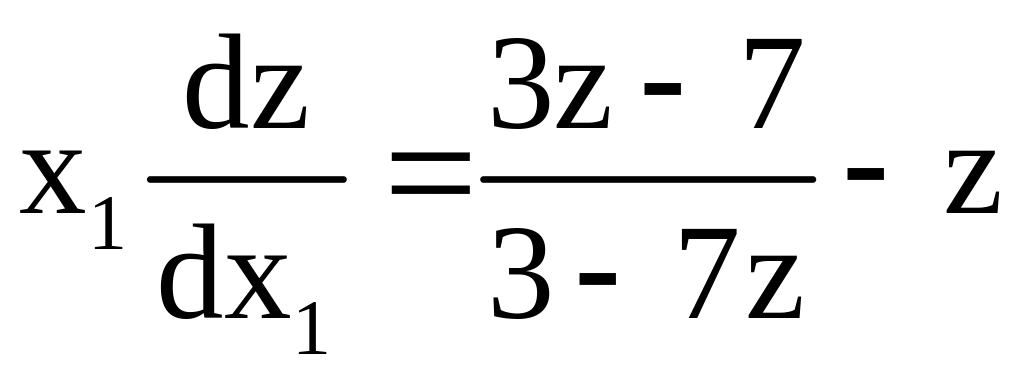
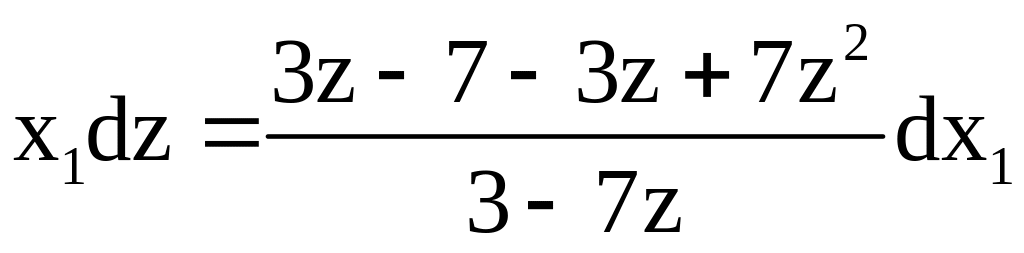
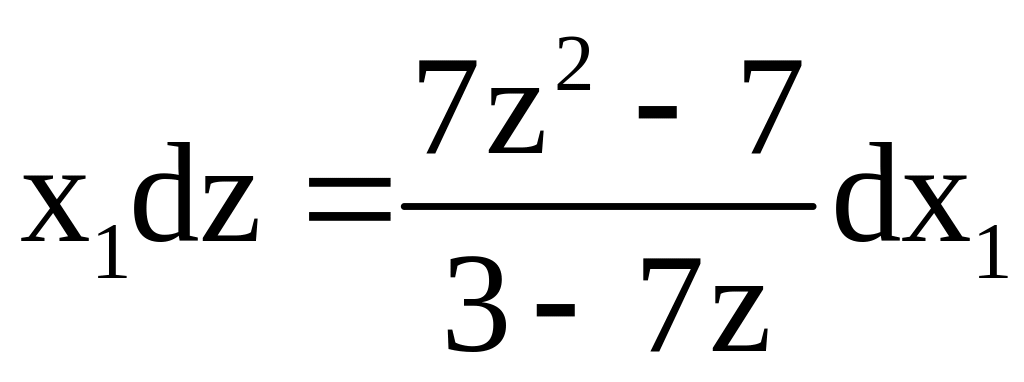
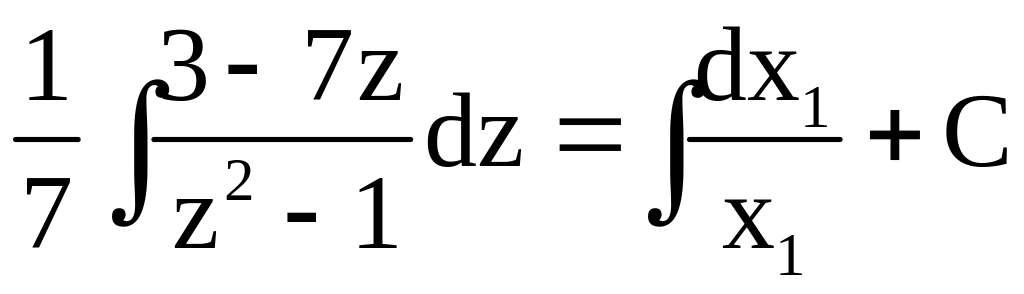
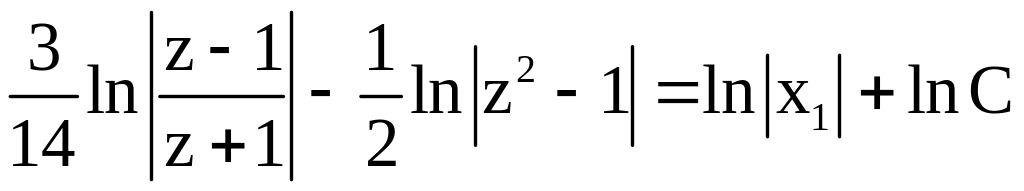
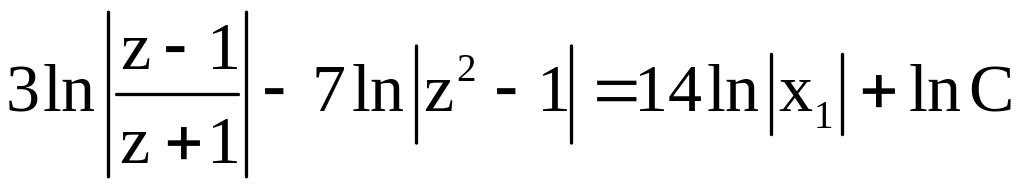
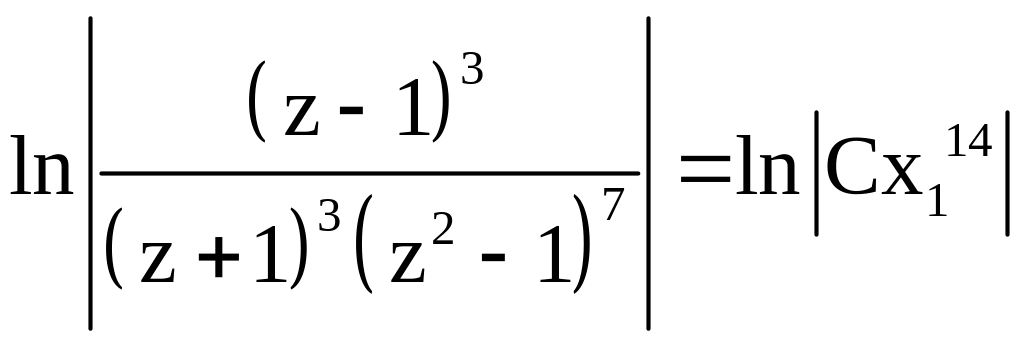
Учитывая, что

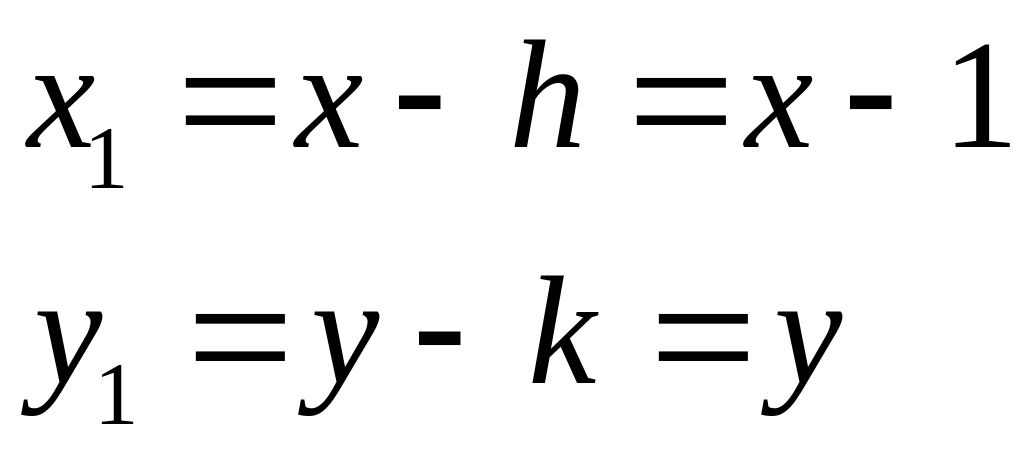
Получим - общее решение

2)

+

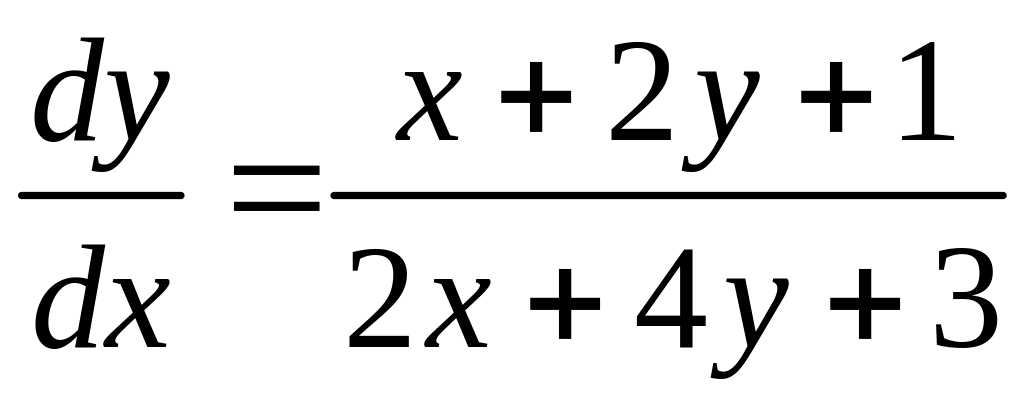
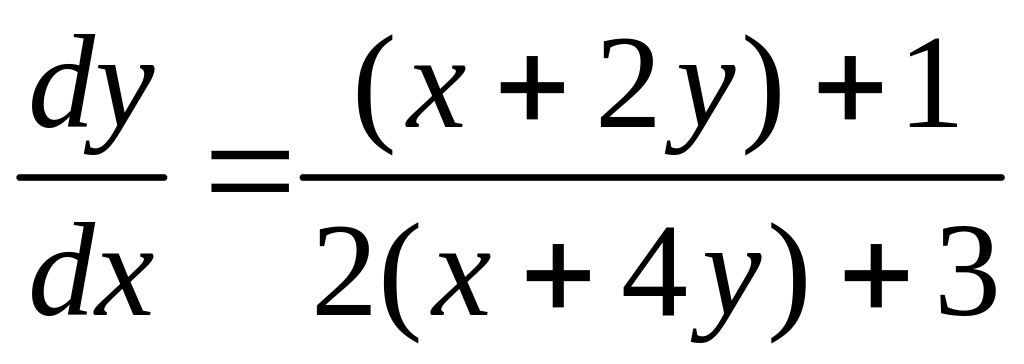
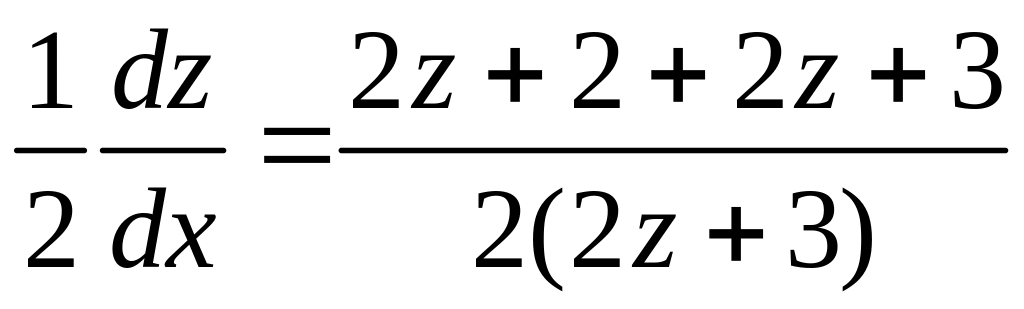
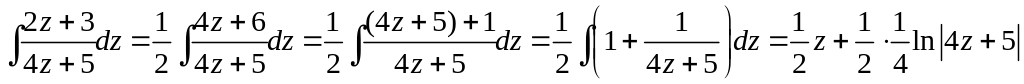
Т.К. , то

Общее решение

3.4 Линейные уравнения первого порядка.

Определение Линейным уравнением первого порядка называется уравнение, линейное относительно неизвестной функции У и ее производной .

- 1

Где , - заданные функции от х (или постоянные)

Рассмотрим следующие методы решения:

1. Метод Бернулли

Неизвестное функцию ищем в виде произведения двух неизвестных функций - 2

-3

Одну из этих функций можно взять произвольной. Выберем функцию и так чтобы - 4 – Это уравнение с разделяющимися переменными

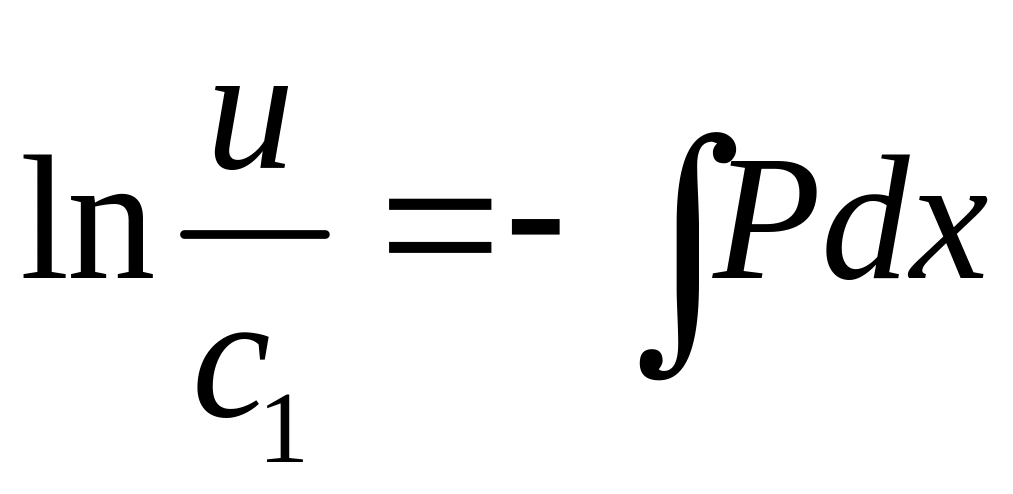
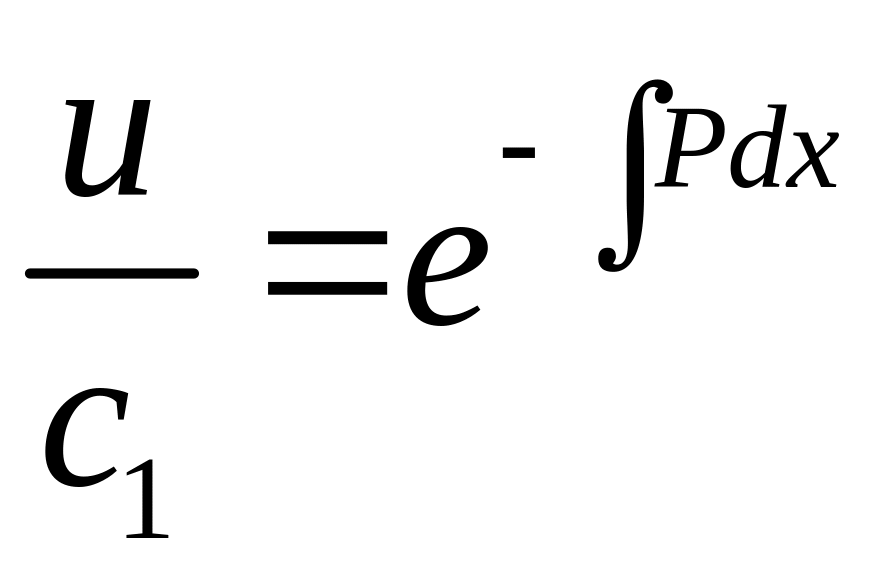
Нам достаточно какого-нибудь отличного от нуля решения уравнения – 4, то возьмем - 5 и подставим в уравнение -3, получим

или

Откуда

Подставляя u uv в формулу в формулу (2), получим

(6)

Замечание Покажем, что решение (6) не изменится, если мы возьмем

т.е. сохраним постоянную С₁

Подставляя в решение (6)

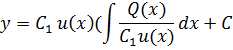
При раскрытии скобок в первом слагаемой С₁ сокращаются, а во втором получаем С₁∙С. Это есть постоянная и ее можно просто обозначить С, т.е. выражение (6) не изменилось.

Пример.

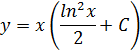
- общее решение

2) Метод Лангранжа – метод вариации произвольной постоянной.

Вместо уравнения (1) рассмотрим уравнение

(7)

Это однородное уравнение, решая его

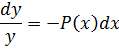
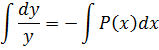
получим уравнение (8)

Оно содержит произвольную постоянную С.

Решение уравнения (1) будем искать в форме (8), полагая, что С – функция от x, т.е.

(9)

дифференцируя, находим

Подставляя y и y’ в уравнение (1), получим

или

откуда

интегрируя получим

где - произвольная постоянная

И, наконец, общее решение уравнения (1) будет

Пример.

решим соответствующее однородное уравнение

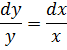
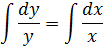
Подставим в данное уравнение

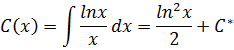
подставим в получим

- общее решение

где С* - const

Замечание. Если х – считать неизвестной функцией, а у – независимой переменной, то линейное уравнение имеет вид

и решается подстановкой где ,