2.2 Разности решетчатых функций

Скорость изменения непрерывной функции f(t) определяется ее первой производной , скорость изменения решетчатой функции f(n) характеризуется ее первой разностью ∆f(n), которая является аналогом первой производной непрерывной функции.

Разность первого порядка, или первая разность решетчатой функции f(n) равна

Геометрически первая разность ∆f(n) представляет собой разность между последующей (n-1)-й и предыдущей n ординатами решетчатой функции. На рис. 15,а показана решетчатая функция и ее первая (рис.15,б) и вторая (рис.15,в) разности.

Рисунок 15

Первая разность, как и первая производная по существу равна отношению приращению функции к приращению аргумента: , и так как , то ее значение равно ∆f(n).

Разность второго порядка представляет собой разность между последующей и данной ∆f(n) разностями первого порядка:

или, если раскрыть первые разности,

Разность к-го порядка

Так, например

В общем случае разность к-го порядка

Пример.

Найти разность 4-го порядка:

2.3 Линейные разностные уравнения

Уравнения вида

(1)

или

(2)

где - постоянные коэффициенты;

- заданная решетчатая функция;

- искомая функция,

называются линейными разностями уравнениями к-го порядка с постоянными коэффициентами.

Уравнение (1), используя формулу для конечных разностей порядка К, можно привести к уравнению (2), причем порядок уравнения (1) определяется порядкрм уравнения (2).

2.4 Определение дискретного преобразования Лапласа (D-преобразования)

Обычное преобразование Лапласа – это преобразование непрерывной функции

(3)

D-преобразование - это преобразование решетчатой функции.

Символа D-преобразования Лапласа приняты и .

Выражение дискретного преобразования Лапласа (D-преобразования) получают из (3), если заменить интеграл суммой, непрерывную функцию - решетчатой функцией , а время t – дискретным аргументом nT:

( 4)

Если в качестве аргумента непрерывной функции принять относительное время и выражение для D-преобразования получит вид

( 5)

Дискретное преобразование для смещенных решетчатых функций имеет вид:

Соответствие между оригиналом и изображением смешенной решетчатой функции записывают так:

Преобразование в и в называется прямым D-преобразованием.

Пример. Задана единичная ступенчатая функция . Определить .

Это выражение является бесконечно убывающей геометрической прогрессией, первый член которой а=1, знаменатель прогрессии . Сумма прогрессии:

(5)

или

2.5 Определение Z-преобразования

Если в выражениях, определяющих D-преобразование, заменить на z, т.е. положить , то получим так называемое Z-преобразование, являющееся рациональной функцией относительно новой переменой z.

D-преобразование и Z-преобразование – совершено эквивалентны. Одним из преимуществ Z-преобразования является сравнительная легкость сравнения обратного преобразования и упрощение записи, поскольку z легче записать, чем или . Выбор того или иного вида преобразования определяется удобством его применения при решении конкретной задачи. называют еще модифицированным Z-преобразованием.

Пример. Пусть , тогда

Сума геометрической прогрессии при

что получают, заменив =z в формуле (5).

2.6 Основные свойства Z-преобразования

Теорема линейности. Пусть и . Тогда , что вытекает из свойства рядов: при сложении рядов их слагаемое складываются, при уменьшении ряда на число все слагаемые умножаются на число.

Теорема дифференцирования по параметру. Если , где а – параметр, тогда

Теоремы смещения независимой переменой в области оригинала.

1. Теорема запаздывания. Если и к – целое положительное число, тогда

2. Теорема опережения. Если и к- целое положительное число, тогда

При

Теорема о начальном значении оригинала.

Теорема о конечном значении.

2.7 Таблица Z-преобразования.

Рассмотрим Z-преобразование (включая модифицированное Z-преобразование) некоторых наиболее встречающихся функций.

1. Пусть .

Тогда

(6)

2. Пусть тогда

Отсюда

Пусть , тогда (7):

(8)

где .

3. Пусть . Получим ее изображение. К выражению

применим теорему дифференцирования по параметру α. Получим

Примем α=0, получим

это и есть модифицированное Z-преобразование функции . Обычное Z-преобразование (ε=0):

4. Дважды продифференцировав функцию (7) по параметру α и приняв α=0 для функции , получим модифицированное Z-преобразование:

Обычное Z-преобразование (ε=0):

Дискретные преобразования приведены в таблице 1.

Таблица 1.

№ п/п	f(t)	F(p)	F(nT)	Z{f(nT)	f [(n+ε)T]	Модифицированное Z{f(n,ε)T} Z-преобразования
1.	1
2.
3.
4.

8. определение оригиналов по формуле разложения

Пусть - правильная дробь, где степень не больше степени . Если степень числителя и знаменателя равны, то выделяют целую часть.

То по формуле разложения

где a_к – полюси функции , т.е. корни знаменателя ;

n_к – кратность полюсов;

к – число полюсов.

Дифференцирование выполняется по Z.

При практическом использовании формулы предел вычисляют так: знаменатель содержит множитель и поэтому может быть представлен в виде:

Тогда

Производная берется по , потом подставляется .

Примеры. Найти оригиналы изображения (или ), применив формулу разложения:

1.

2.

3. ;

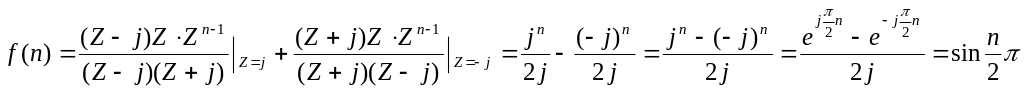
4.

8. решение разностных уравнений

Рассмотрим методику решения разностных уравнений, записанных в виде:

Применяя к разностному уравнению Z-преобразования и пользуясь теоремой опережения, получают операторное уравнение, из которого находят изображение искомой функции . Далее, пользуясь таблицей или формулой разложения. Находят искомую решетчатую функцию . Если начальные значения заданы, то находят частное решение разностного уравнения. Если начальные условия разностного уравнения не заданы, то, считая их произвольными постоянными, получают общее решение.

Пример. Решить разностные уравнения

1. задано однородное разностное уравнение

Определим его изображение, используя теорему опережения:

корни знаменателя

Находим решение , используя теорему разложения

2. Задано неоднородное разностное уравнение

Определяют изображение уравнения, используя теорему опережения при нулевых начальных условиях:

Отсюда

Для получения оригинала используют теорему разложения для случая, когда кратность корней равна

3 передаточные функции дискретных систем

1.3 передаточная функция разомкнутой системы

Введем понятие типовой импульсной цепи, куда входят идеальный импульсный элемент («ключ») и непрерывная часть рисунок 16

Рисунок 16

Сигнал на выходе является непрерывным и не равным нулю между дискретными моментами времени. Чтобы рассмотреть динамику этой цепи (ее входной и выходной сигналы только в дискретные моменты времени ), условно на вход цепи подключают фиктивный дискретизатор (квантователь), работающий синхронно с входным квантователем.

Тогда динамические свойства импульсной цепи можно характеризовать при помощи дискретной передаточной функции (д.п.ф.):

где д.п.ф. – это отношение Z-преобразования выходного сигнала к Z-преобразованию входного сигнала при нулевых начальных условиях.

3.2 Точный способ определения д.п.ф.

Д.п.ф. импульсной системы связана с весовой функцией непрерывной части Z-преобразованием

или этому соответствует условная запись

Чтобы вычислить д.п.ф. , надо:

1. определить передаточную функцию приведенной непрерывной части и разложить ее на простейшие дроби ;

2. найти импульсные переходные функции с помощью обратного преобразования Лапласа для каждой составляющей ;

3. перейти к решетчатым функциям и взять Z-преобразование для каждой составляющей.

Условная запись действий (1, 2, 3):

В большинстве случаев дискретных систем ФЭ создает импульсы прямоугольной формы, относительно длительности с периодом повторения Т (рисунок 17):

Рисунок 17

Передаточная функция формирующего элемента прямоугольной формы:

Если длительность импульсов существенно меньше основных постоянных времени остальных звеньев системы, то , т.е. формирующий элемент может быть приближено заменен безинерционным звеном.

При , т.е. , формирующий элемент выдает в течении всего периода повторения Т постоянный сигнал.

В данном (наиболее распространенном) случае ФЭ называется фиксирующим (запоминающим) с передаточной функцией .

Фиксацию сигнала на постоянном уровне рассматривают как экстраполяцию полиномом нулевого порядка, тогда ФЭ (при ) называется экстраполятором нулевого порядка.

Передаточная функция приведенной непрерывной части системы:

Дискретная передаточная функция

где

Передаточную функцию можно выразить через передаточную функцию , если применить теорему смещения из теории Z-преобразования.

Тогда получим:

Пользуясь этой формулой, при переходе от решетчатых функций к их Z-преобразованию берут модифицированное Z-преобразование и вместо подставляют , т.е. .

Если относительная длительность импульса (экстраполятор нулевого порядка), тогда

определяется обычным порядком (п. 1, 2, 3).

Пример. Определим дискретную передаточную функцию системы, состоящую из ИЭ прямоугольных импульсов длительностью с периодом повторения Т и непрерывной части с передаточной функцией:

Передаточная функция приведенной непрерывной части системы

Дискретная передаточная функция

Определим д. п. ф. , для чего дробь представим в виде суммы элементарных дробей:

Пользуясь таблицей Z – преобразований (ε = 0), определим

где ;

Дискретная передаточная функция системы

Рассмотренный способ получения д. п. ф. является точным и для реальных систем высокого порядка реализовать его затруднительно.

3.3 Приближенные способы определения д. п. ф.

При практических расчетах импульсных систем с фиксатором (экстраполятором нулевого порядка) используют приближенные способы перехода от функций к д. п. ф. , которые основаны на замене первой производной по времени, имеющей место в непрерывных системах, первой разностью в дискретных системах.

Рассмотрим интегрирующее звено непрерывной системы:

Перейдем к первой разности от первой производной:

Перейдем к Z – преобразованию:

Последняя формула используется для приближенного перехода от передаточных функций непрерывной части (без учета фиксатора) к д. п. ф.: .

Более точный переход от непрерывной системы к дискретной обеспечивает подстановка Тастина

Пример. Определить точную и приближенные д. п. ф. разомкнутой системы, состоящей из «ключа», фиксатора и идеального интегрирующего звена (рисунок 18).

Рисунок 18

1. Определение точной д. п. ф.:

2. Определение д. п. ф. подстановкой

3. Определение д. п. ф. подстановкой Тастина

3.4 Дискретная передаточная функция и характеристическое уравнение замкнутой системы

Рассмотрим замкнутую систему САУ (рисунок 19):

Рисунок 19

Д.п.ф. замкнутой системы определяется так же, как и в непрерывных системах.

Передаточная функция замкнутой системы через передаточную функцию разомкнутой системы

.

Характеристическое уравнение дискретной системы

.

Передаточная функция ошибки

.

Пример. Определить характеристики замкнутой дискретной АУ, которая в разомкнутом виде соответствует системе в предыдущем примере:

Характеристическое уравнение замкнутой системы:

4. анализ устойчивости дискретных сау

По аналогии с непрерывными системами дискретная САУ устойчива, если переходные процессы в ней затухают с течением времени, т.е. система устойчива, если свободная составляющая переходного процесса с течением времени затухает:

.

Свободная составляющая является решением однородного разностного уравнения

Решение последнего уравнения при различных корнях, т.е. отсутствие одинаковых корней представляет сумму

(9)

где - постоянные интегрирования, зависящие от начальных условий;

- корни характеристического уравнения.

При на плоскости Z получается окружность с R=1/

Из выражения (9) следует, что при решение в том случае, если все корни по модулю меньше единицы, т.е.

Отсюда общее условие устойчивости: для устойчивости дискретной системы необходимо и достаточно, чтобы все корни характеристического уравнения системы находились внутри круга единичного радиуса с центром в начале координат (рисунок 20).

Рисунок 20

Если хотя бы один корень располагается на окружности единичного радиуса, то система находиться на границе устойчивости, при , система не устойчива. Таким образом, окружность с в плоскости корней играет ту же роль, что и мнимая ось в плоскости корней .

Для определения устойчивости дискретной системы на практике обычно не вычисляются корни характеристического уравнения, а применяются косвенные методы исследования устойчивости – критерии.

Однако, прежде чем пользоваться критериями устойчивости непрерывных систем для исследования устойчивости дискретных систем, надо выполнить соответствующее преобразование характеристического уравнения дискретной системы. Из теории ФКП с помощью билинейного преобразования единичный круг в комплексной плоскости . Поэтому, чтобы отобразить единичный круг плоскости в левую часть комплексной плоскости надо в характеристическом уравнении замкнутой дискретной системы выполнить подстановку .

Условием устойчивости импульсной системы является расположение всех корней преобразованного характеристического уравнения дискретной системы в левой части плоскости .

Благодаря – преобразованию все критерии устойчивости непрерывных систем могут быть использованы для определения устойчивости дискретных систем.

4.1 Аналог критерия устойчивости Гурвица

Для устойчивости замкнутой дискретной системы необходимо и достаточно, чтобы все определителей Гурвица, составленных из коэффициентов преобразованного характеристического уравнения, были больше нуля:

Пример. Критерием Гурвица исследовать на устойчивость, систему, рассмотренную раньше, которая в замкнутом виде описывается характеристическим уравнением

Выполним подстановку

где .

Для этого уравнения условие устойчивости Гурвица заключается в положительности коэффициентов, т.е.

Отсюда пределы изменения передаточного коэффициента

.

4.2 Частотные критерии устойчивости

Выражение для частотных характеристик дискретных систем получаются из их передаточных функций заменой . Они описываются трансцендентными выражениями, их определение связано со сложными расчетами, поэтому на практике частотные характеристики применяются относительно псевдочастоты. Переход к псевдочастоте основан – преобразовании, т.е.

или ,

где - относительная псевдочастота.

Как видно, периодичность частотных характеристик, дискретных АИС при переходе к псевдочастоте, исчезает, поскольку при псевдочастота , а комплексная частота изменяется по всей оси от до . Поэтому для передаточной функции с – преобразованием можно использовать обычные критерии устойчивости, справедливые для непрерывных систем.

Удобно использовать абсолютную псевдочастоту , которая приблизительно равна круговой частоте на частотах, где выполняется условие

Отсюда . Тогда .

Частотные характеристики, построенные в функции абсолютной псевдочастоты, практически совпадают с частотными характеристиками, построенными в функции круговой частоты и определяются выражением:

при .

Построение частотных характеристик дискретных систем в области абсолютной частоты практически ничем не отличается от построения этих характеристик непрерывных систем в области круговой частоты.

Критерий устойчивости Михайлова. При использовании критерия Михайлова в характеристический полином замкнутой системы подставляют , заменяют от 0 до и в комплексной плоскости строит годограф . Замкнутая дискретная система устойчива, если при возрастании от 0 до вектор повернется против часовой стрелки, нигде не обращаясь в ноль, на угол . Если кривая Михайлова проходит через начало координат, то система находится на границе устойчивости (рисунок 21).

Рисунок 21

Кривую Михайлова можно построить относительно псевдочастоты . Формулировка критерия аналогична.

Пример. Исследовать на устойчивость замкнутую систему АИС, характеристическое уравнение которой имеет вид

1. Годограф Михайлова (рисунок 22) построим, используя подставку , тогда

значения частоты принимаем: (таблица 2).

Таблица 2

ω	0	π/6	π/4	π/3	π/2	2π/3	3π/4	5π/6	π
U(ω)	3	2.86	2.7	2.5	2	1.5	1.3	1.14	1
V(ω)	0	0.5	0.7	0.86	1	0.86	0.7	0.5	0

Рисунок 22

Замкнутая АИС неустойчива.

2. Годограф Михайлова (рисунок 23) построим относительно псевдочастоты λ:

; ; ; ; ; ; .

Рисунок 23

Замкнутая АСР неустойчива.

Критерий устойчивости Найквиста. Строят АФХ или W(λ) разомкнутой системы (рисунок 24).

Рисунок 24

Если АФХ устойчивой разомкнутой системы не охватывает точку с координатами (-1; j0), то замкнутая система устойчива (точки 1, 2, 3 соответствуют характеристикам САУ устойчивой, на границе, неустойчивости).

Пример. Критерием Найквиста исследовать замкнутую систему на устойчивость, если ДПФ разомкнутой системы имеет вид:

, k=2; T=1 с.

а) Кривую Найквиста (АФЧХ разомкнутой АИС) построим, используя подстановку :

Кривую Найквиста построим (рисунок 25), задаваясь частотой ; ; (таблица 3)

Таблица 3

ω	0	π/6	π/4	π/3	π//2
Р(ω)	-1, 0	-1, 0	-1, 0	-1, 0	-1, 0
Q(ω)	∞	1,7	-1, 0	0,6	0

Рисунок 25

Замкнутая АИС находится на границе устойчивости.

б) Кривую Найквиста построим (рисунок 26) относительно псевдочастоты λ:

К=2; Т=1с ;

Таблица 4

λ	0	0,5	1	2	4	∞
Ρ(λ)	-1	-1	-1	-1	-1	-1
Q(λ)	∞	-4	-2	-1	-0,5	0

Рисунок 26

Замкнутая АИС находится на границе устойчивости.

Логарифмический критерий устойчивости. В области псевдочастоты λ методика ЛЧХ ничем не отличается от методики построения их в области круговой частоты:

.

Отсюда ЛАХ и ЛФХ (рисунок 27)

.

Устойчивость дискретных систем может быть оценена логарифмическим частотным критерием устойчивости: для устойчивости замкнутой АИС необходимо, чтобы точка пересечения ЛАХ с осью lg λ (частота среза λ_с) была левее точки пересечения ЛФХ с линей –π.

Рисунок 27