
3.2 Ориентированный граф
Для ориентированного графа существуют аналогичные определения. Отметим некоторые из них)
Путем
называется последовательность дуг
.(δ1,
δ2,
…, δn)
вида
δі
=(![]() ),
i=
1, 2, …, n
(рис.
3.9а).
),
i=
1, 2, …, n
(рис.
3.9а).
Число дуг, образующих путь, называется длиной пути.
Путь называется составным, если в нем повторяется хотя бы одна дуга (рис.3.9б), сложным - хотя бы одна вершина (рис.3.9в), и простым - в противном случае (рис.3.9а).
Контуром называется путь, концевые вершины которого совпадают (рис.3.9г). Все вершины контура имеют степень s( ) ≥ 2.
Граф G = < \/, U > называется сильно связаным, если любая пара вершин соединена путем.
Максимальный по включению вершин сильно связный подграф графа называется его компонентой сильной связности.
Рис.3.9
Граф называется несильно связным, если число его компонент сильной связности больше 1.
Для того, чтобы определить связность ориентированного графа, не нужно обращать внимание на ориентацию дуг. То есть для ориен-тированного графа существуют понятия как связности, так и сильной
связности.
Пример 6. Какой из графов, показанных на рис.3.10, является
сильно
связным, а какой несильно связным?
□
Граф, изображенный на рис.3.10б, является
несильно связным, т.к.,
например, вершины
![]() и
и
![]() не
соединены путем. Этот граф имеет
две компоненты сильной связности с
носителями соответствен-
не
соединены путем. Этот граф имеет
две компоненты сильной связности с
носителями соответствен-
но
![]()
Граф, изображенный на рис. З.10а, является сильно связным, т.к. любая пара его вершин соединена путем.
Рис. 3.10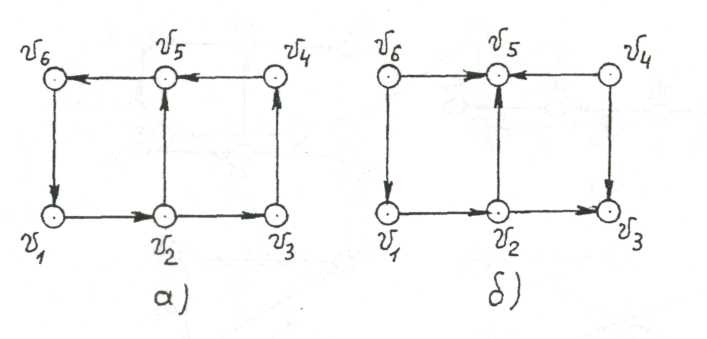
а) найдите все пути и простые пути от вершины а к вершине е ;
б) определите все простые контуры графа G .
3. Является
ли неориентированный граф G
< V,
U
> , у
которого
![]()
![]() ,
связным?
Укажите ребро, являющееся мостом.
,
связным?
Укажите ребро, являющееся мостом.
В графе G (рис.3.12) измените направления дуг таким образом, чтобы он преобразовался в бесконтурный граф.
Является ли ориентированный граф G < V, U >, у которого
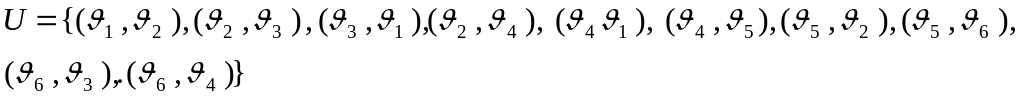
связным, сильно связным?
Задачи для самостоятельного решения
I. Выполните следующие упражнения с графом G (рис.3.11):
а) найдите какие-либо цепи длины 5 и длины 8 между вершинами и . б) определите все цепи и простые цепи между вершинами и ;
в) определите все простые циклы графа G.


4. ЦИКЛОМАТИКА
4.1. Основные определения
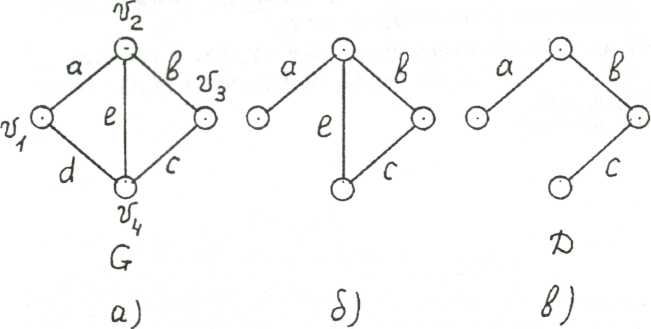
Деревом называется связный граф, не содержащий циклов. Остовом называется суграф, являющийся деревом. Пример I. Задан граф G < V, U > (рис.4.1а). Построить какой-либо остов графа.
Если граф G содержит К компонент связности, то его цик- ломатическое число
ν(G) = m - п + К. (4.2)
Цикломатическое число несвязного графа может быть определено как сумма цикломатических чисел его компонент связности:
ν(G)
=![]() (4.3)
(4.3)
 Пример
2. Определить цикломатическое число
(G)
графа G,
заданного
в примере 1.
□ Так как остов D
графа
G
имеет две хорды d
и e
,
то
Пример
2. Определить цикломатическое число
(G)
графа G,
заданного
в примере 1.
□ Так как остов D
графа
G
имеет две хорды d
и e
,
то
ν(G) = 2.
Для определения ν(G) можно воспользоваться формулой (4.1). Заданный связный граф G имеет т = 5 ребер и n =4 вер-шин. По формуле (4.1) получаем:
ν(G) = m - n + 1 = 5 - 4 + 1 = 2. ■
Пример
3. Определить цикломатическое число
ν(G)
графа G
= <V,
U
>
у которого
![]()
![]()
Рис. 4.1.
□ Удалим в графе G, например, ребро d. В результате получим суграф, который не является деревом, т.к. присутствует цикл (b,c,е).(рис.4.1б). Удалим дополнительно ребро е . В этом случае получим суграф, не имеющий циклов, т.е. получим дерево, которое будет являться остовом D (рис.4.1в). ■ Хордой остова D в связном графе G называется всякое ребро графа, не принадлежащее остову D .
Так в примере 1 хордами остова D являются ребра d и e .
Любая часть графа, которая состоит из хорды и остова, имеет точно один цикл.
Цикломатическое число ν(G) графа G равно числу хорд любого остова в G.
 Если
связный граф G
имеет n
вершин и m
ребер,
то
ν(G)
= m
- n
+ 1 (4.1.)
□
Граф
изображен
на
рис
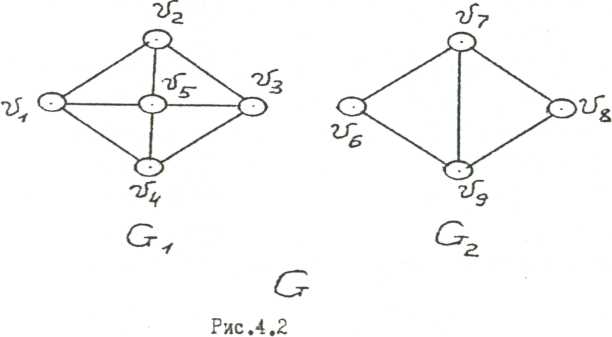
.4.2. Из
рисунка
Если
связный граф G
имеет n
вершин и m
ребер,
то
ν(G)
= m
- n
+ 1 (4.1.)
□
Граф
изображен
на
рис
.4.2. Из
рисунка
видно, что граф G является несвязным и состоит из двух компонент связности G и G . Для определения ν(G) воспользуемся формулой (4.2). Граф G имеет m =13 ребер, n -9 вершин и К =2 компонент связности, поэтому
ν(G)
= m
- n
+
К
=13
-9+2= 6.
Цикломатическое число ν(G)
можно
определить по формуле (4.3):
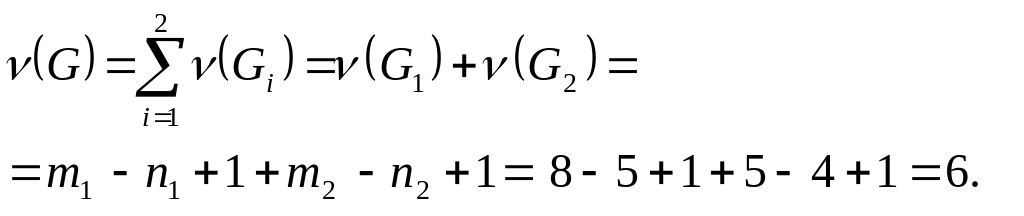 Если
граф состоит из нескольких компонент
связности, каждая из которых является
деревом, то такой граф называется лесом.
Если
граф состоит из нескольких компонент
связности, каждая из которых является
деревом, то такой граф называется лесом.
Если лес G имеет n вершин и К компонент связности, то он содрежит т = n - К ребер.
Остовным лесом называется граф, каждая компонента которого яв-ляется остовным деревом.
Коциклический ранг χ(G) (ранг разреза) графа - это число ребер в его остовном лесе:
χ (G) = n - К . (4.4)
Пример 4. Построить какой-либо остовный лес для графа G , рассмотренного в примере 3. Определить коциклический ранг χ (G) графа G.
□ Один из возможных остовных лесов D графа G показан на рис.4.3. Здесь D1 - один из возможных остовов

Рис. 4.3
компоненты связности G1, а D2 компоненты связности Gг .
Определим χ (G)графа G по формуле (4.4). Имеем n = 9 вершин и К =2 компонент связности графа G:
χ (G) = п - К = 9 - 2 = 7.
Если пересчитать число ребер т в остовном лесе D , то получим m =7. ■
Теорема 4.1. Граф является двудольным тогда и только тогда, да все его циклы имеют четную длину. Звездный граф К1,n является деревом. Любое дерево является двудольным графом.
