§ 5. Плотность графа

В кластерном анализе, при информационном поиске и других практических задачах используется понятие плотности графа.

Кластер – (англ. пучок, группа) наименьший участок жесткого или флоппи-диска (дискета); при фрагментации задействованные (несущие информацию) и свободные кластеры все более перемешиваются, что отрицательно сказывается на быстродействии компьютера; для упорядочения распределения кластера используются программа – дефрагментация.

Плотностью графа называется максимальная мощность носителя полного подграфа К графа G и обозначается :

.

Другими словами, максимальное число попарно смежных вершин графа G является плотностью этого графа.

Следовательно, для определения плотности графа G необходимо выделить в графе G все полные подграфы.

Алгоритм выделения полных подграфов

1. Сопоставляем корню строящегося дерева заданный граф G .

2. Фиксируем в графе вершину с максимальной степенью, сопоставив ее концу дуги, исходящей из корня. Строим исходящие из корня дуги, число которых равно ( мощность носителя неокрестности вершины v₀ ). Конец каждого из этих дуг взаимно однозначно сопоставляем вершине неокрестности .

3. Каждый конец построенных дуг взвешиваем окрестностью вершины графа, сопоставленного рассматриваемому корню.

4. Считаем конец построенного яруса корнем нового дерева.

5. Устанавливаем, взвешена ли вершина символом Ø . Если “нет”, то переходим к п.2, если “да” – то к п.6.

6. Каждая ветвь построенного дерева однозначно определяет полный подграф заданного графа G .

Закон поглощения. Если в k – ом ярусе дерева вершины v_i и v_j смежны, поддерево с корнем v_i построено и если в поддереве с корнем v_j появляется вершина v_i , то соответствующая ветвь не строится.

Пример. Определить плотность графа G (рис. 5.10).

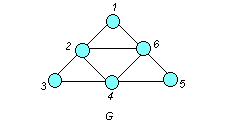
Рис. 5.10

□ Используя алгоритм выделения полных подграфов, построим искомое дерево (рис. 5.11).

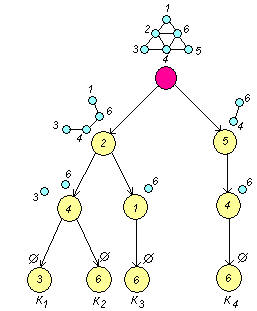
Рис. 5.11

Здесь K_i – полные подграфы. Видно, что мощность носителей всех подграфов равна трем, значит

Каждое множество состоит из попарно смежных вершин. ■

§ 6. Раскраска графа

К построению раскрасок графов сводится целый ряд практических задач, например, задачи составления расписаний, распределения оборудования, проектирования некоторых технических изделий.

Раскраской вершин графа называется разбиение носителя V графа G на подмножества, при котором каждое подмножество V_i не содержит ни одной пары смежных вершин.

Каждому подмножеству сопоставляется цвет, в который окрашивают элементы этого подмножества.

Хроматическим числом графа G называется минимальное число п (число красок), для которого граф имеет п – раскраску.

Если = п , то граф называется п – хроматическим .

Если (т – число красок и раскраска удовлетворяет определению), то граф называется т – раскрашиваемым .

1 – хроматический граф – это пустой граф.

Теорема 1. Граф является 2 – хроматическим тогда и только тогда, когда он не содержит циклов нечетной длины.

Двудольный граф – 2-хроматический граф.

Любое дерево – 2-хроматический граф.