Оценки хроматического числа

Теорема 2. Если максимальная степень вершин графа G равна , то

Теорема 3. Граф G с максимальной степенью вершин является s - раскрашиваемым, за исключением двух случаев:

1. при граф содержит компоненту , являющуюся полным графом плотности

2. при граф G содержит компоненту, являющуюся циклом нечетной длины.

Оценки, полученные с помощью этих теорем, дают хорошее приближение лишь тогда, когда степени всех вершин графа имеют близкие значения. В противном случае оценка может быть значительно завышена.

Теорема 4. Для любого графа

где вершинное число независимости графа.

Алгоритм минимальной раскраски вершин графа

1. Выделяем множество пустых подграфов графа G.

2. Строим двумерную таблицу, каждой строке которой сопоставим взаимно однозначно пустой подграф, столбцу – вершину; в клетке записываем единицу, если j-ая вершина содержится в i-ом пустом подграфе, в противном случае клетку оставляем пустой.

3. Определяем покрытия столбцов строками. Каждое покрытие порождает раскраску. Покрытие минимальной мощности определяет хроматическое число графа G.

Пример. Определить хроматическое число графа G, изображенного на рис. 5.12

Рис. 5.12

□ Для определения хроматического числа сначала необходимо выделить все пустые подграфы заданного графа G. Используя алгоритм выделения пустых подграфов, построим дерево (рис.5.13).

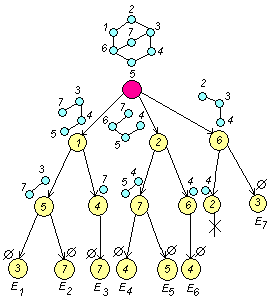
Рис. 5.13

Строим двумерную таблицу:

1 2 3 4 5 6 7

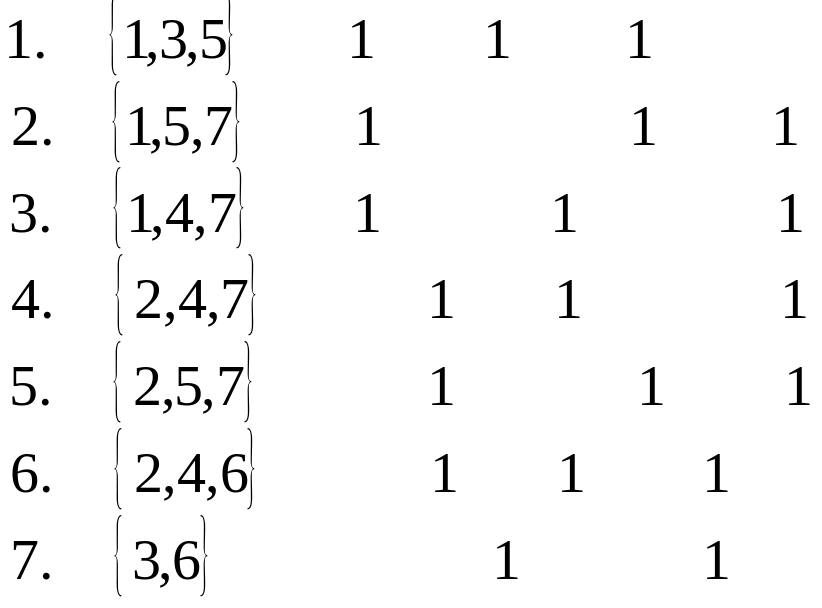
Определяем минимальное число строк, покрывающих все столбцы таблицы. Такими строками могут быть строки 1, 4, 7. Значит

Зададимся красками: для множествами вершин синяя (Син), для множества вершин краска красная ( Кр ), для множества вершин краска зеленая ( Зел ) .

Раскрасим вершины графа G :

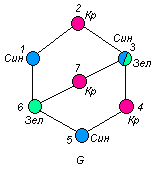
Отметим, что вершину 3 можно раскрасить в два цвета: синий или зеленый. ■

Замечание. Аналогично можно определить раскраску ребер графа G и найти минимальную раскраску ребер этого графа G .

§ 7. Планарность графа

Планарность графов играет существенную роль при проектировании коммуникаций и связи между объектами на плоскости: дороги между населенными пунктами, водопроводные и газопроводные сети, линии электропередач, межсоединения на печатных платах и кристаллах интегральных схем и т.д.

Граф называется планарным (плоским ), если существует изоморфный ему граф, который может быть изображен на плоскости без пересечения ребер.

Свойства планарности не нарушаются, если некоторое ребро разбить на два ребра введением вершины второй степени или заменить два ребра, инцидентных вершине второй степени, одним ребром, удалив эту вершину.

Два графа называются гомеоморфными (изоморфными с точностью до вершины второй степени), если после удаления из них вершин второй степени и объединения инцидентных этим вершинам ребер, они оказываются изоморфными.

Граф, гомеоморфный планарному графу, также является планарным.

Пример. Являются ли графы G и G₁ (рис. 5.14) гомеоморфными?

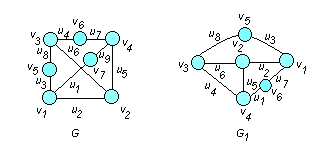
Рис. 5.14

□ Графы G и G₁ являются гомеоморфными, т.к. после удаления в графе G вершин второй степени и объединения инцидентных этим вершинам ребер u₃ и u₈ , u₄ и u₇ , u₁ и u₉ и после удаления в графе G₁ вершин второй степени и объединения инцидентных этим вершинам ребер u₃ и u₈ , u₁ и u₇ , графы G и G₁ оказываются изоморфными ( см. Глава ΙV, рис. 4.4 ). ■

Теорема (Л.С.Понтрягина). Граф планарен тогда и только тогда, когда он не содержит подграфа, гомеоморфного К₅ или К_3,3 .

Граф К₅ – минимальный полный граф, который не является планарным (рис. 5.15). Удаление одного ребра делает этот граф планарным.

Граф К_3,3 – минимальный полный двудольный граф, который не является планарным (рис. 5.15). Удаление одного ребра делает этот граф планарным.

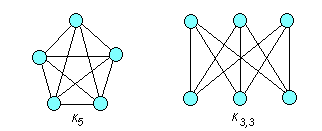
Рис. 5.15

Толщиной графа G называется наименьшее число планарных графов, объединение которых дает граф G.

Толщина планарного графа равна 1.

Нижняя оценка толщины графа определяется неравенством

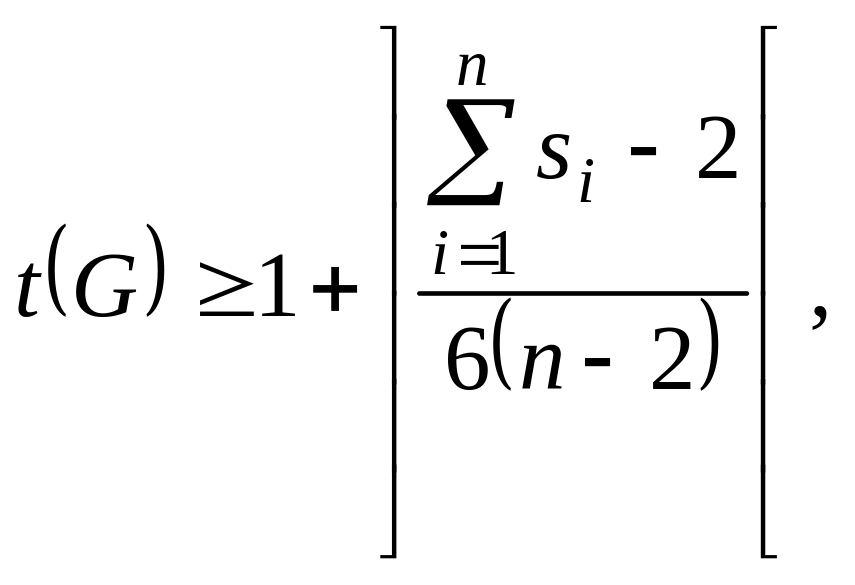
где ] [ - ближайшее целое число, степень i-ой вершины.

Замечание. Для строгого доказательства планарности графа используется теорема Понтрягина, а указанное неравенство лишь только нижняя оценка толщины графа.

Пример. Является ли граф G (рис. 5.16) планарным? Если нет, то определить, какие ребра необходимо удалить (реализовать на других плоскостях) для преобразования графа G в планарный.

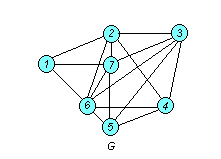
Рис. 5.16

□ Согласно теореме Понтрягина проверяем граф G на содержание подграфа, гомеоморфного К₅ .

Проверку можно сделать следующим образом: удаляя минимальное количество вершин и некоторое количество ребер, попытаться привести заданный граф G к виду графа К₅ . В приведенном графе могут присутствовать вершины второй степени.

В заданном графе G можно не удалять ни одной из вершин. Преобразования показаны на рис. 5.17

Рис. 5.17

В результате получили подграф, гомеоморфный К₅ , т.е. заданный граф G не является планарным. Удаление любого ребра в полученном подграфе делает его (подграф) планарным.

Теперь проверим граф G на содержание подграфа, гомеоморфного К_3,3 . Попытаемся привести граф G к виду К_3,3 .

В графе К_3,3 все вершины имеют степень, равную 3. В графе G степень вершин больше или равна 3, поэтому в процессе преобразования графа G вершины удалять не будем. Сведение графа G к виду графа К_3,3 показано на рис. 5.18

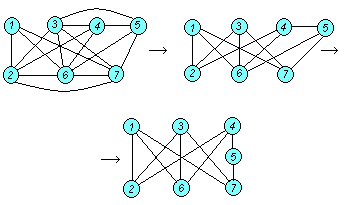
Рис. 5.18

В результате получен подграф, гомеоморфный К_3,3 . Удаление любого ребра в полученном подграфе делает его планарным.

Вывод: заданный граф G содержит подграфы, гомеоморфные К₅ и К_3,3. Следовательно, заданный граф G не является планарным.

Определим нижнюю оценку толщины графа G :

,

т.е. .

Так как удаление любого ребра из каждого полученного подграфа выводит их из класса подграфов, гомеоморфных К₅ или К_3,3 , то граф G станет планарным, если удалить ребро, входящее как в подграф, гомеоморфный К₅ , так и в подграф, гомеоморфный К_3,3. Таким множеством общих ребер является множество

.

Удаление любого из этих ребер делает заданный граф G планарным.

После удаления, например, ребра получаем планарный граф, плоское представление которого изображено на рис. 5.19.

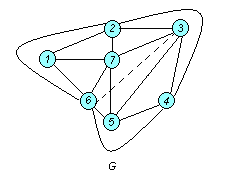
Рис. 5.19

Соединение, которое соответствует удаленному ребру (показано пунктирной линией), реализуется на второй плоскости. Толщина графа G равна двум. ■