
- •1 Методические указания
- •1.1 Понятия неопределённого интеграла. Свойства
- •1.2 Непосредственное интегрирование
- •1.3 Метод подстановки
- •1.4 Вычисление интегралов типа
- •1.5 Вычисление интегралов типа
- •1.6 Метод интегрирования по частям
- •1.7 Интегрирование рациональных функций
- •1.8 Интегрирование некоторых классов иррациональных функций
- •1.9 Интегрирование тригонометрических функций
- •1.10 Тригонометрические подстановки
- •2 Нулевой вариант
- •3 Решение 0 варианта
- •4 Расчетные задания
1 Методические указания
1.1 Понятия неопределённого интеграла. Свойства
В
курсе дифференциального исчисления
решалась задача: по данной функции
 найти её производную
найти её производную
 (или дифференциал
(или дифференциал
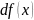 ).
Интегральное исчисление решает обратную
задачу: найти функцию
).
Интегральное исчисление решает обратную
задачу: найти функцию
 ,
зная её производную
,
зная её производную
 (или
дифференциал
(или
дифференциал
 ).
Искомая функция
называется первообразной функции
).
Искомая функция
называется первообразной функции
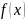 .
.
Функция
называется первообразной функции
на интервале
 ,
если для любого
,
если для любого


Множество
всех первообразных функций
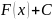 для функции
называется неопределённым интегралом
от функции
и обозначается символом
для функции
называется неопределённым интегралом
от функции
и обозначается символом
 ,таким образом
,таким образом
 .
.
Операция нахождения неопределённого интеграла от функции называется интегрированием этой функции.
1.2 Непосредственное интегрирование
При вычислении интегралов следует пользоваться таблицей интегралов
 +C,
+C,
 .
11
.
11

 12
12

 13
13

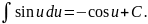 14
14

 15
15

 16
16





и свойствами.
Если под интегралом стоит алгебраическая сумма, то интеграл суммы равен сумме интегралов:

Постоянный множитель можно выносить за знак интеграла и вносить под знак интеграла:

где А – постоянная величина. (Переменную величину выносить за знак интеграла нельзя).
3

4

Пример
1 Вычислить
интеграл

Решение. Применяем формулу I, полагая в ней u=x, n=4;
получаем:

Пример
2 Вычислить
интеграл
 .
.
Решение.

Пример
3 Вычислить
интеграл

Решение. Возводим двучлен в квадрат и затем интегрируем:

1.3 Метод подстановки
Если
под знаком интеграла стоит выражение
 ,
,
т.
е. даётся произведение элементарной
функции от некоторой функции на
дифференциал последней, например,
 ,
,
 то
интеграл вычисляют методом подстановки,
используя свойство инвариантности если
то
интеграл вычисляют методом подстановки,
используя свойство инвариантности если
 ,
где
,
где
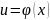 непрерывная дифференцируемая функция
аргумента
непрерывная дифференцируемая функция
аргумента
 .
.
Пример
4 Вычислить
интеграл

Решение.
Полагаем
 ,
отсюда
,
отсюда

Выполнив подстановку, получаем:

Пример
5 Вычислить
интеграл

Решение.
Вводим
подстановку
 отсюда
отсюда
 Пользуемся
подстановкой и получаем:
Пользуемся
подстановкой и получаем:

Если подинтегральное выражение можно представить в виде произведения степени (с показателем n, не равным минус единице) на дифференциал основания, то интеграл следует вычислять по формуле:

Пример
6

Если
подинтегральное выражение можно
представить в виде дроби, в числителе
которой стоит дифференциал знаменателя,
т.е. дроби вида
 ,
то интеграл следует вычислять по формуле:
,
то интеграл следует вычислять по формуле:

Пример
7

Если
подинтегральное выражение можно
представить в виде дроби со знаменателем
 и числителем
и числителем
 (в числителе должен стоять дифференциал
основания квадрата второго члена
знаменателя), то интеграл следует
вычислять по формуле:
(в числителе должен стоять дифференциал
основания квадрата второго члена
знаменателя), то интеграл следует
вычислять по формуле:

Пример
8

Если
подинтегральное выражение можно
представить в виде дроби со знаменателем
 и числителем
,
то интеграл следует вычислять по формуле:
и числителем
,
то интеграл следует вычислять по формуле:
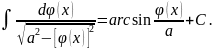
(В числителе дроби должен стоять дифференциал основания квадрата второго члена.)
Пример
9

Если
подинтегральное выражение может быть
представлено в виде дроби со знаменателем
 и числителем
,
то интеграл следует вычислять по формуле:
и числителем
,
то интеграл следует вычислять по формуле:

Пример
10

Если
подинтегральное выражение может быть
представлено в виде дроби с знаменателем
 и числителем
,
то интеграл следует вычислять по формуле:
и числителем
,
то интеграл следует вычислять по формуле:

Пример
11
 =
(в числителе стоит дифференциал основания
квадрата второго члена)=
=
(в числителе стоит дифференциал основания
квадрата второго члена)=

