4. Двойственные задачи

Каждой задаче линейного программирования можно поставить в соответствие задачу, называемую двойственной.

Запишем общую задачу линейного программирования

→max

(4.1)

Двойственной задачей к задаче (4.1) называется задача

(4.2)

В таком случае задача (4.1) называется прямой. Исходная и двойственная задачи образуют пару взаимно двойственных задач, при этом любую из них можно рассматривать как прямую задачу.

Переход от прямой задачи к двойственной можно осуществить с помощью следующих правил.

1. Каждому ограничению – неравенству со знаком ≤ соответствует неотрицательная неизвестная y_i двойственной задачи, а каждому ограничению – равенству неизвестная произвольного знака.

2. Каждой неотрицательной неизвестной х_j прямой задачи соответствует ограничение – неравенство со знаком ≥ двойственной задачи, а каждой произвольной по знаку переменной – ограничение в виде равенства.

3. Матрица коэффициентов при неизвестных системы ограничений двойственной задачи получается транспонированием матрицы коэффициентов при неизвестных системы ограничений прямой задачи.

4. Свободные коэффициенты системы ограничений равны соответствующим коэффициентам при неизвестных х_j целевой функции прямой задачи.

5. Коэффициенты при неизвестных y_i целевой функции L двойственной задачи равны свободным коэффициентам системы ограничений прямой задачи.

6. Если целевая функция z прямой задачи максимизируется, то целевая функция L двойственной задачи минимизируется, и наоборот, если целевая функция z прямой задачи минимизируется, то целевая функция L двойственной задачи максимизируется.

Отметим, что число ограничений прямой задачи равно числу неизвестных двойственной задачи, а число ограничений двойственной задачи равно числу неизвестных прямой задачи. В связи с этим двойственную задачу обычно выгоднее решать, чем исходную прямую, если в прямой задаче имеется большое количество ограничений и малое число неизвестных.

Справедливы следующие утверждения.

1. Двойственная задача (4.2) имеет решение в том и только в том случае, если имеет решение прямая задача (4.1).

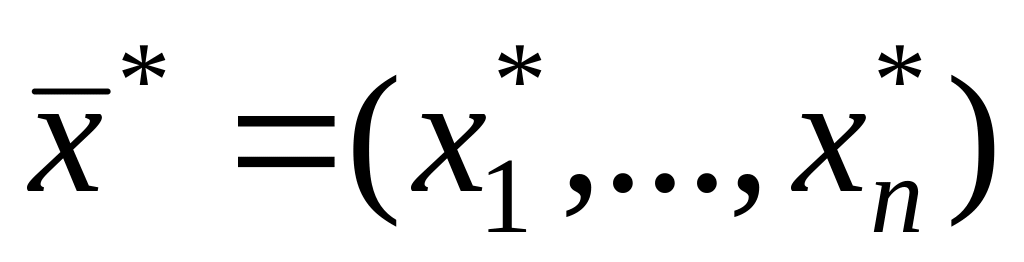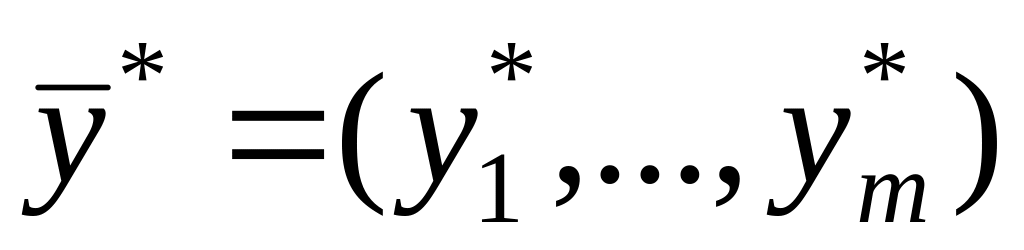2. Если есть оптимальное решение прямой задачи (4.1), а есть оптимальное решение двойственной задачи (4.2), то выполняется соотношение двойственности

(4.3)

3. Если получено решение одной из пары двойственных задач, например, прямой, то оптимальное решение другой задачи определяется равенством

(4.4)

где С_о – матрица - строка коэффициентов целевой функции Z перед базисными неизвестными оптимального решения прямой задачи, W – матрица коэффициентов при базисных неизвестных оптимального решения в системе ограничений прямой задачи.

4. Если прямая исходная задача не содержит ограничений в виде равенств, то между оптимальными решениями прямой и двойственной задач и элементами симплекс – таблиц, соответствующих этим решениям, существует следующая взаимосвязь

.

(4.5)

В качестве примера найдем неотрицательные значения х₁ и х₂, максимизирующие функцию

(4.6)

при наличии ограничений

(4.7)

с помощью перехода к двойственной задаче.

Используя сформулированные выше правила, перейдем к двойственной задаче

(4.8)

(4.9)

Перейдем к канонической задаче. Для этого перенесем свободные коэффициенты в левые части неравенств (4.9) и обозначим получившиеся выражения за новые неизвестные

,

.

Кроме того, перейдем к задаче на максимум. Для этого поменяем знаки в правой части целевой функции (4.8). Каноническая задача имеет вид:

; (4.10)

(4.11)

Для решения задачи симплекс – методом необходимо привести систему (4.11) к единичному базису и найти опорное решение. Умножим равенства (4.11) на (-1). Тогда получим

(4.12)

В полученной системе неизвестные y₃ и y₄ выражаются через y₁ и y₂.

Тем самым, система приведена к единичному базису. Приравнивая, свободные неизвестные y₁ и y₂ к нулю, получим базисное решение.

y₁=0; y₂=0; y₃=-5; y₄=-4.

Так как базисные неизвестные отрицательны, полученное решение не является опорным. Для нахождения опорного решения воспользуемся методом исключений Жордана – Гаусса. Выпишем коэффициенты системы (4.12) в таблицу

	y1	y2	y3	y4
y3	-4	-3	1	0	-5
y4	-3	-4	0	1	-4

Умножим первую строку на (-1) и прибавим ко второй строке. При этом y₃ перестает быть базисной неизвестной.

	y1	y2	y3	y4
	4	3	-1	0	5
y4	1	-1	-1	1	1

В выбранной первой строке содержатся два положительных коэффициента при неизвестных. Выберем за разрешающий второй столбец. В разрешающем столбце только один положительный элемент, равный 3, в первой строке. Поэтому первую строку считаем разрешающей строкой. Разрешающий элемент, расположенный на пересечении разрешающей строки и разрешающего столбца равен 3. Разделим разрешающую строку на разрешающий элемент

	y1	y2	y3	y4
	4/3	1	-1/3	0	5/3
y4	1	-1	-1	1	1

Получим нуль в разрешающем столбце. Для этого ко второй строке прибавим разрешающую. При этом неизвестная y₂, соответствующая разрешающему столбцу, становится базисной и пишется в символьном столбце

	y1	y2	y3	y4
y2	4/3	1	-1/3	0	5/3
y4	7/3	0	-4/3	1	8/3

Полученной таблице соответствует система равенств

или

(4.13)

Эта система приведена к единичному базису и базисное решение, соответствующее этой системе является опорным

y₁=0; ; y₃=0; (4.14)

Выразим целевую функцию L₁ через свободные неизвестные y₁ и y₃. Для этого подставим равенства (4.13) в (4.10). Тогда задача (4.10); (4.11) с учетом (4.13) примет вид

;

Составим симплекс – таблицу

	y1	y2	y3	y4
y2	4/3	1	-1/3	0	5/3
y4	7/3	0	-4/3	1	8/3
L1	-8	0	8	0	-40

В последней строке в первом столбце имеется отрицательная оценка. Следовательно, опорное решение (4.14), соответствующее записанной таблице, не оптимально. Выберем первый столбец за разрешающий. Разделим элементы последнего столбца на соответствующие положительные элементы разрешающего столбца

; .

Наименьший результат соответствует второй строке, поэтому выберем эту строку за разрешающую. Разрешающий элемент равен 7/3. Разделим разрешающую строку на разрешающий элемент.

	y1	y2	y3	y4
y2	4/3	1	-1/3	0	5/3
y4	1	0	-4/7	3/7	8/7
L1	-8	0	8	0	-4

Получим нули в разрешающем столбце. Для этого из первой строки вычтем разрешающую, умноженную на 4/3, а к последней прибавим разрешающую, умноженную на 8.

После пересчета имеем

	y1	y2	y3	y4
y2	0	1	3/7	-4/7	1/7
y1	1	0	-4/7	3/7	8/7
L1	0	0	24/7	24/7	-216/7

В последней строке отрицательных оценок (коэффициентов при неизвестных y_i) нет. Следовательно, опорное решение, соответствующее полученной таблице оптимально.

; ; y₃=0; y₄=0; . (4.15)

Определим решение прямой задачи (4.6); (4.7), используя формулу (4.4)

.

Здесь - матрица - строка.

Учтем, что базисными неизвестными в оптимальном решении являются y₁ и y₂, и элементами матриц С_о и W являются коэффициенты при базисных неизвестных оптимального решения в равенствах (4.8) и (4.11). То есть

С_о=(24 24);

В этом случае обратная матрица W^-1 имет вид

Отсюда

.

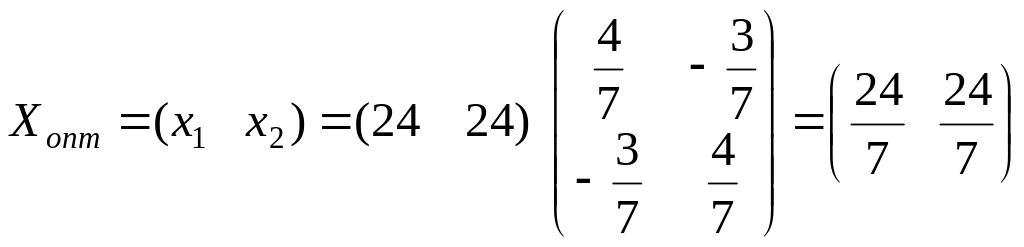Таким образом, оптимальное решение (4.6), (4.7) следующее

(4.16)

; ; .

Заметим, что прямая исходная задача (4.6), (4.7) не содержит ограничений в виде равенств, поэтому оптимальное решение (4.16) может быть записано сразу без использования формулы (4.4). Для этого можно воспользоваться равенствами (4.5)

,

,

где b₃ и b₄ – элементы последней строки симплекс–таблицы, соответствующей оптимальному решению.