
- •Задания для самостоятельной работы
- •Тема 21. Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами
- •21.1. Общее решение линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами
- •21.2. Общее решение линейного неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами
- •21.3. Математическая модель рынка с прогнозируемыми ценами
- •Задания для решения на практическом занятии
- •Задания для самостоятельной работы
- •Раздел III Теория вероятностей
- •Тема 22. Элементы комбинаторики
- •Задания для решения на практическом занятии
- •Задания для самостоятельной работы
- •Тема 23. Случайное событие и его вероятность
- •23.1. События и отношения между ними
21.2. Общее решение линейного неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами
Теорема 2. Общее решение линейного
неоднородного дифференциального
уравнения (21.1) можно представить в виде
суммы общего решения соответствующего
линейного однородного дифференциального
уравнения (21.2) и некоторого частного
решения
![]() неоднородного уравнения (21.1).
неоднородного уравнения (21.1).
Замечание. Для решения линейного неоднородного дифференциального уравнения второго порядка может быть применен общий метод вариации произвольных постоянных (см. [1, гл. 12, 12.8], [33, ч. 2, гл. 4, § 3], [35, гл. 4]). Но для достаточно большого числа случаев может быть использован метод подбора частного решения по виду правой части.
Теорема 3. Пусть
дано дифференциальное уравнение
![]() .
Если функция
является частным решением уравнения
.
Если функция
является частным решением уравнения
![]() ,
а функция
,
а функция
![]() – частным решением уравнения
– частным решением уравнения
![]() ,
то функция
,
то функция
![]() является частным решением
.
является частным решением
.
Алгоритм поиска общего решения линейного неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами
1) Найти общее решение соответствующего однородного уравнения (21.2).
2) Подобрать частное решение неоднородного уравнения (21.1) в соответствии с правилом подбора частного решения по виду правой части.
Пусть
![]() ,
где
,
где
![]() – известный многочлен степени
– известный многочлен степени
![]() .
Если
.
Если
![]() не является корнем характеристического
уравнения, то частное решение следует
искать в виде
не является корнем характеристического
уравнения, то частное решение следует
искать в виде
![]() ,
где
,
где
![]() – многочлен степени
с пока неизвестными коэффициентами.
Если
является простым корнем характеристического
уравнения, то частное решение следует
искать в виде
– многочлен степени
с пока неизвестными коэффициентами.
Если
является простым корнем характеристического
уравнения, то частное решение следует
искать в виде
![]() .
Если
является корнем характеристического
уравнения кратности 2, то частное решение
следует искать в виде
.
Если
является корнем характеристического
уравнения кратности 2, то частное решение
следует искать в виде
![]() .
Подставляя
.
Подставляя
![]() в уравнение (21.2) и приравнивая коэффициенты,
стоящие слева и справа при одинаковых
степенях
в уравнение (21.2) и приравнивая коэффициенты,
стоящие слева и справа при одинаковых
степенях
![]() ,
найти коэффициенты многочлена
.
,
найти коэффициенты многочлена
.
Пусть
![]() или
или
![]() ,
где
– многочлен степени
.
Если
,
где
– многочлен степени
.
Если
![]() не являются комплексно-сопряженными
корнями характеристического уравнения,
то частное решение следует искать в
виде
не являются комплексно-сопряженными
корнями характеристического уравнения,
то частное решение следует искать в
виде
![]() ,
где
и
,
где
и
![]() – различные многочлены степени
с пока неизвестными коэффициентами.
Подставляя
в уравнение (21.2) и приравнивая коэффициенты,
стоящие слева и справа сначала
соответственно при синусах и косинусах,
а затем при одинаковых степенях
,
найти коэффициенты многочленов
и
.
– различные многочлены степени
с пока неизвестными коэффициентами.
Подставляя
в уравнение (21.2) и приравнивая коэффициенты,
стоящие слева и справа сначала
соответственно при синусах и косинусах,
а затем при одинаковых степенях
,
найти коэффициенты многочленов
и
.
3) Записать общее решение неоднородного уравнения (21.1). Записать ответ.
Пример 4. Найти
общее решение дифференциального
уравнения
![]() .
.
Решение. Данное дифференциальное уравнение является линейным неоднородным дифференциальным уравнением второго порядка с постоянными коэффициентами.
1) Выпишем соответствующее линейное
однородное дифференциальное уравнение:
![]() .
Его характеристическое уравнение имеет
вид
.
Его характеристическое уравнение имеет
вид
![]() ,
его корни
,
его корни
![]() ,
,
![]() .
В соответствии с правилом фундаментальная
система решений состоит из функций
.
В соответствии с правилом фундаментальная
система решений состоит из функций
![]() ,
,
![]() .
Общее решение линейного однородного
дифференциального уравнения:
.
Общее решение линейного однородного
дифференциального уравнения:
![]() .
.
2) Правая часть линейного неоднородного
дифференциального уравнения представляет
собой многочлен второй степени и может
быть представлена следующим образом:
![]() .
Так как
.
Так как
![]() является простым корнем характеристического
уравнения, то в соответствии с правилом
подбора решения по виду правой части
частное решение линейного неоднородного
дифференциального уравнения следует
искать в виде произведения многочлена
второй степени с пока неизвестными
коэффициентами на переменную
,
то есть в виде
является простым корнем характеристического
уравнения, то в соответствии с правилом
подбора решения по виду правой части
частное решение линейного неоднородного
дифференциального уравнения следует
искать в виде произведения многочлена
второй степени с пока неизвестными
коэффициентами на переменную
,
то есть в виде
![]() ,
где
,
и
– некоторые неопределенные вещественные
коэффициенты. Найдем первую и вторую
производные от частного решения
,
где
,
и
– некоторые неопределенные вещественные
коэффициенты. Найдем первую и вторую
производные от частного решения
![]() ,
получим
,
получим
![]() ,
,
![]() .
Подставим частное решение
и его производные в линейное неоднородное
дифференциальное уравнение
,
тогда
.
Подставим частное решение
и его производные в линейное неоднородное
дифференциальное уравнение
,
тогда
![]() или
или
![]() .
.
Приравнивая коэффициенты при одинаковых степенях , получим систему линейных алгебраических уравнений для определения коэффициентов , и :
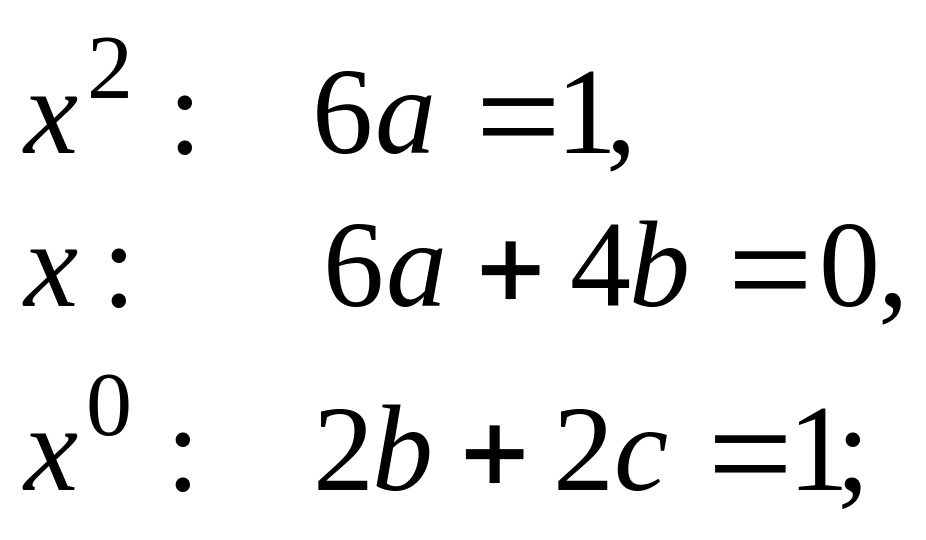
![]()
Следовательно, искомое частное решение имеет вид
![]() .
.
3) Таким образом, по
теореме 2 общее решение исходного
линейного неоднородного дифференциального
уравнения:
![]() .
.
Пример 5. Найти решение задачи Коши
линейного дифференциального уравнения
![]() ,
,
![]() ,
,
![]() .
.
Решение. Данное дифференциальное уравнение является линейным неоднородным дифференциальным уравнением второго порядка с постоянными коэффициентами.
1) Выпишем соответствующее линейное
однородное дифференциальное уравнение:
![]() .
Его характеристическое уравнение имеет
вид
.
Его характеристическое уравнение имеет
вид
![]() ,
его корни
,
,
его корни
,
![]() .
В соответствии с правилом фундаментальная
система решений состоит из функций
.
В соответствии с правилом фундаментальная
система решений состоит из функций
![]() ,
,
![]() .
Общее решение линейного однородного
дифференциального уравнения:
.
Общее решение линейного однородного
дифференциального уравнения:
![]() .
.
2) Правая часть линейного неоднородного
дифференциального уравнения представляет
собой произведение многочлена первой
степени на функцию
![]() :
:
![]() .
Так как
.
Так как
![]() не является корнем характеристического
уравнения, то в соответствии с правилом
подбора решения по виду правой части
частное решение линейного неоднородного
дифференциального уравнения следует
искать в виде произведения многочлена
первой степени с пока неизвестными
коэффициентами на функцию
,
то есть в виде
не является корнем характеристического
уравнения, то в соответствии с правилом
подбора решения по виду правой части
частное решение линейного неоднородного
дифференциального уравнения следует
искать в виде произведения многочлена
первой степени с пока неизвестными
коэффициентами на функцию
,
то есть в виде
![]() ,
где
и
– некоторые неопределенные вещественные
коэффициенты. Найдем первую и вторую
производные от частного решения
,
получим
,
где
и
– некоторые неопределенные вещественные
коэффициенты. Найдем первую и вторую
производные от частного решения
,
получим
![]() ,
,
![]() .
.
Подставим частное решение и его производные в линейное неоднородное дифференциальное уравнение , получим равенство
![]() ,
,
которое после сокращения на и приведения подобных слагаемых примет вид
![]()
Приравнивая коэффициенты при одинаковых степенях , получим систему линейных алгебраических уравнений для определения коэффициентов и :
![]()
Следовательно, искомое частное решение
имеет вид
![]() .
.
3) Таким образом, по теореме 2 общее
решение исходного линейного неоднородного
дифференциального уравнения
![]() .
.
Найдем решение задачи Коши. Для этого
найдем производную от общего решения:
![]() ,
а затем подставим начальные условия
,
в общее решение и его производную:
,
а затем подставим начальные условия
,
в общее решение и его производную:
![]() или
или
![]()
Получили систему линейных алгебраических
уравнений для определения
и
.
Решая ее, получаем
![]() ,
,
![]() .
Тогда искомое частное решение примет
вид
.
Тогда искомое частное решение примет
вид
![]() .
.
