6.3. Методы классификации наблюдений в случае

двух генеральных совокупностей с известным распределением вероятностей

6.3.1. Случай, когда известны априорные вероятно­сти. Теперь мы перейдем к проблеме отыскания областей R и R₂, при которых достигается минимум средних потерь (см. (5) § 6.2). Поскольку априорные вероятности известны, мы можем найти совместные распределения вероятностей для генеральной совокупности и для множества наблюден­ных случайных величин. Вероятность того, что при наблю­дении над генеральной совокупностью , каждая величина будет меньше соответствующей компоненты векторау, равна

(1)

— Можно определить также условную вероятность того, что наблюдение производилось над определенной генеральной совокупностью при условии, что наблюдаемые величины имеют данные значения. Например, условная вероятность того, что наблюдение произведено над генеральной совокуп­ностью при условии, что его результаты составляют век­торх, равна

. (2)

Предположим, что С(1|2) = С(2|1)= 1. Тогда математиче­ское ожидание потерь будет равно

(3)

Это вероятность неправильной классификации. Следова­тельно, нам нужно сделать эту вероятность минимальной. Для данного результата наблюдения х мы достигаем ми­нимума вероятности неправильной классификации, выбирая ту генеральную совокупность, которой соответствует наи­большая условная вероятность. Если

(4)

то мы заключаем, что выборка была произведена из гене­ральной совокупности . В противном случае мы отдаем предпочтение генеральной совокупности ₂. Поскольку мы достигаем минимума вероятности ошибочной классификации в каждой точке, то мы тем самым достигаем минимума ее и во всем пространстве. Таким образом, правило состоит в следующем:

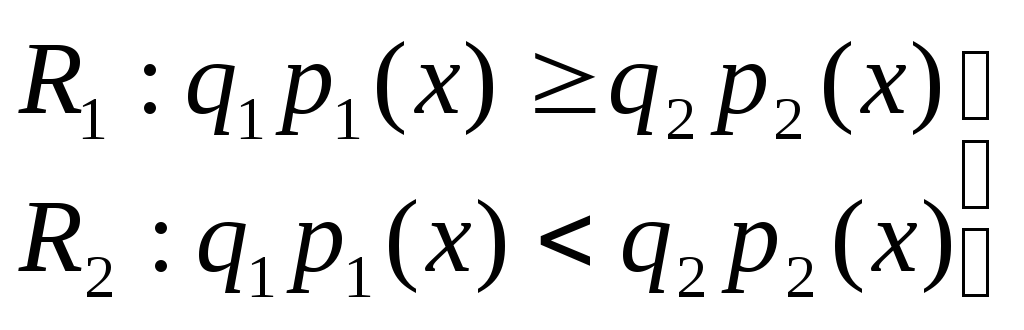(5)

Если , то точку л: можно отнести и к и к ₂. Мы можем договориться отнести ее, например, к R₁. Если для данного х , то точка также может быть отнесена к любой из двух областей.

Теперь формально покажем, что (5) является наилучшим

методом. Для любого метода R* = () вероятностьнеправильной классификации равна

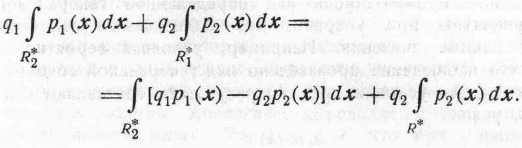(6)

Второй член правой части есть фиксированное число; пер­вый член будет минимальным, если включает в себя та­кие точки x, для которых < 0, и исклю­чает точки х, для которых > 0. Если мы предположим, что

(7)

то метод Бейеса будет единственным с точностью до мно­жеств нулевой вероятности.

Заметим, что математически задача состоит в следующем. Для данных неотрицательных чисел q₁ и q и неотрицатель­ных функций p₁(x) и р₂(х) найти такие области R и R₂, чтобы (3) было минимальным. Решение этой задачи дается соотношениями (5). Если нам нужно найти минимум вели­чины (5) § 6.2, которую можно записать в виде

(8)

то, поскольку [С (2|1)q] и [С(1|2)q₂] — неотрицательные константы, R и R₂ нужно выбрать согласно следующим условиям:

(9)

можно записать по-другому:

(10)

Теорема 6.3.1. Пусть q₁ и q— априорные вероят­ности того, что наблюдение производится над гене­ральной совокупностью ₁ с плотностью распределения вероятностей р₁(х) и над генеральной совокупностью ₂ с плотностью р(х) соответственно. Пусть, далее, цена ошибочной классификации наблюдения, производимого над, равна С (2|1), а цена ошибочной классификации наблюдения, производимого над , равна С(1|2). Тогда области классификации R₁ и R₂, определяемые из ус­ловия (10), дают минимум математического ожидания потерь. Если

(11)

то такой метод является единственным с точностью до множеств нулевой вероятности.

6.3.2. Случай, когда априорные вероятности неиз­вестны. Во многих случаях классификации статистик не мо­жет приписать априорные вероятности двум генеральным со­вокупностям. В этом случае мы отыскиваем класс допусти­мых методов, т. е. множество методов, которые не могут быть улучшены.

Сначала докажем, что метод Бейеса является допусти­мым. Пусть R = (R₁ R₂)— метод Бейеса для данных q_l ,q₂. Существует ли метод R* = (,R} такой, что P(1|2, R*)P(1|2,R) и P(2|1, R*)P(2|1, R), причем хотя бы одно из этих неравенств является строгим? Так как R—метод Бейеса, то

P(2|1,R)+P(1|2,R)P(2|1,)+. (12)

Это неравенство может быть переписано в виде

(13)

Предположим, что q₁ > 0. Тогда, если P(l |2,R*)P(1|2, R), то правая часть (13) меньше или равна нулю и, следовательно, P(2|1,R)P(2| 1,R*). Если q₂>0, то из P(2| 1,R*)P(2|1,R) аналогично получаем Р(1|2,R)P(1|2, R*). Таким образом, R* не лучше R и R*—допустимый метод. Если q₁ = 0, то из (13) следует, что 0P(1|2,R*) — P(1|2, R), В методе Бейеса R₁включает лишь точки, для которых р₂ (х) = 0. Следовательно, P(1|2, R) = 0, и если R* должно быть лучше R, то P(1|2, R*) = 0. Если Р{p₂(x) = 0| } =0, тоP(2|1,R) =P{p(x)>0|}= 1.Если P(1|2,R*) = 0, то R* вклю­чает лишь точки, для которых р₂ (х) = 0. Поэтому P(2|1, R*) = P{R|}= Р{>0|₁} = 1, и значит, R* не лучше, чем R..

Теорема 6.3.2. Если Р {p₂(x) = 0|₁} =0 и P{= 0|₂} = 0, то любой метод Бейеса является допу­стимым.

Теперь докажем обратное утверждение, что любой до­пустимый метод является методом Бейеса. Предположим, что¹)

P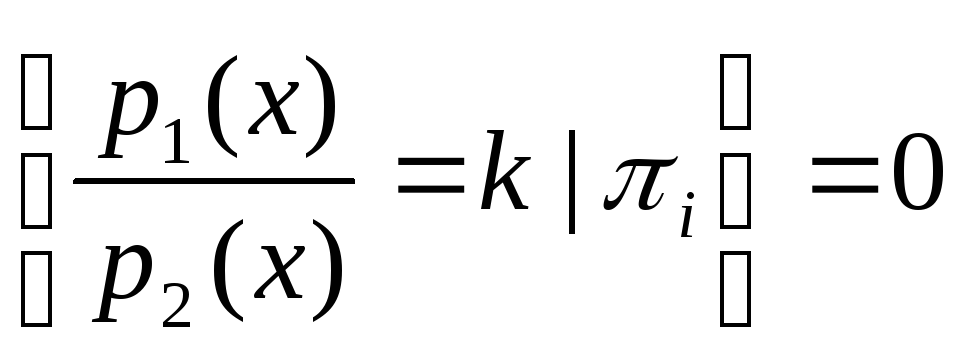 , 0 (14)

Тогда для любого q₁ метод Бейеса является единственным. Кроме того, функция распределения вероятностей (x)/p₂(x) для и ₂ является непрерывной.

Пусть R — допустимый метод. Тогда существует такое k, что

P(2|1,R)=P=P(2|1,R*),

где R* — метод Бейеса, соответствующий тому, что q/q_l = k [т. е. = 1/(1+k)]. Так как метод R является допусти­мым, то Р(1|2,R)P(1|2,R*). Однако в силу теоремы 6.3.2 метод R* является допустимым, и потому Р(1|2, R)P(1|2, R*), т. е. P(1|2, R) = P(1|2,R*). Следовательно, R — также метод Бейеса. Вследствие единствен­ности метода Бейеса R совпадает с R*.

Теорема 6.3.3. Если (14) верно, то любо:1 допу­стимый метод является бейесовым.

Доказательство теоремы 6.3.3. показывает, что класс методов Бейеса является полным, поскольку для любого ме­тода R, не входящего в этот класс, можно построить ме­тод Бейеса R* так, чтобы было P(2|1, R) = P(2|1,R*). Вследствие того, что метод R* является допустимым, P(1|2, R)P(l|2, R*). Более того, класс бейесовых методов является минимальным полным классом, так как он со­впадает с классом допустимых методов.

Теорема 6.3.4. Если (14) верно, то класс методов Бейеса является минимальным полным классом.

Наконец, рассмотрим минимаксный метод. Пусть Р()=P(|j,R), где R—метод Бейеса, соответствующий q. P() есть непрерывная функция . Когда q₁ изменяется от 0 до 1, Р(2|1, ) изменяется от 1 до 0, аP(1|2, ) — от 0 до 1. Поэтому существует такое значениеq₁ скажем q, что P(2|1,q)=P(l|2,q). Это значение q определяет ми­нимаксный метод, так как если бы существовал другой ме­тод R* такой, что max{P(2|1,R*), P(1|2,R*)}Р(2|1,)= Р(1|2,), то это противоречило бы тому, что любой метод Бейеса является допустимым.