6.4. Классификация наблюдений в случае двух генеральных совокупностей, имеющих известные многомерные нормальные распределения

Теперь мы используем общий метод, описанный выше, для случая двух многомерных нормальных генеральных со­вокупностей с равными ковариационными матрицами, а именно для совокупностей с законами распределения N() и N(), где— вектор среднего зна­ченияi-ой генеральной совокупности (i=1,2), a — кова­риационная матрица каждой совокупности. [Этот метод впер­вые был использован Валь дом [1]. Тогдаi-я плотность распределения вероятностей будет равна

(1)

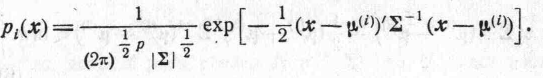
Отношение плотностей равно

(2)

Область , при попадании в которую наблюдение классифи­цируется как наблюдение над, является множеством век­торов x, для которых величина (2) больше k (k выбирается подходящим образом). Так как логарифмическая функция монотонно возрастает, то неравенство (2) эквивалентно не­равенству (получающемуся из (2) переходом к логарифмам)

(3)

Левую часть (3) можно представить в виде

(4)

Группируя соответствующие члены, получаем

. (5)

Первый член является хорошо известной дискриминантной функцией. Это линейная функция компонент вектора резуль­татов наблюдений.

Следующая теорема является прямым следствием тео­ремы 6.3.1.

Теорема 6.4.1. Если имеет плотность распре­деления вероятностей (1) (i=1,2), то области наилуч­шей классификации определяются следующим образом:

(6)

Если априорные вероятности q₁ и q известны, то k равно

⁽⁷⁾

В частном случае двух равновероятных генеральных сово­купностей, которым соответствуют одинаковые цены С(1|2) и C(2|l), k=1 и lnk = 0. Поэтому область, при попадании в которую выборка рассматривается как выборка из , определяется следующим образом:

(8)

Если нам неизвестны априорные вероятности, то мы можем выбрать In k = с, например, из условия, чтобы ма­тематические ожидания потерь, связанных с ошибками классификации, были равны. Пусть X—случайное наблю­дение. Нам нужно найти распределение случайной величины

(9) считая сначала, что X распределен N(,), а затем что X распределен N(, ). ЕслиX распределен N(,), то величина U распределена нормально с математическим ожи­данием

(10)

и дисперсией

(11)

Будем называть «расстоянием» между N(,) и N(⁽²⁾, ) величину

. (12)

Тогда, если X распределен N(, ), то U будет распре­делена N(). Если же X распределен N(⁽²⁾, ), то

(13)

Дисперсия U будет такой же, как и в случае, когда X распределен , поскольку она зависит лишь отмоментов второго порядка случайного вектора X. Таким образом, U будет распределен .

Вероятность ошибочной классификации при условии, что наблюдение производилось над равна

(14)

а вероятность ошибочной классификации при условии, что наблюдение производилось над ₂, равна

(15)

На рис. 9 эти две вероятности изображены в виде заштри­хованных площадей, ограниченных «хвостами» плотностей. Для минимального решения с выбирается так, чтобы

(16)

Теорема 6.4.2. Если (i=1,2) имеют плотности распределения вероятностей (1), то минимаксные об­ласти классификации определяются по (6), где с = 1nk выбирается из условия (16), a C(i|j) — цены ошибочных классификаций.

В случае, когда цены ошибочных классификаций не равны

Следует отметить, что если цены ошибочных классифи­каций равны между собой, то c=0 и вероятность ошибоч­ной классификации равна

между собой, с может быть определено достаточно точно по таблицам нормального распределения методом проб и ошибок.

Оба слагаемых в (5) содержат вектор

. (18) который получается как решение уравнения

. (19)

полученное эффективным численным методом, как, например, метод сокращения Дулиттла.

Интересно отметить, что х'является линейной функ­цией, которая дает максимум

(20)

при любом выборе d. Числитель (20) равен

(21)

а знаменатель

d'M(X — MХ)(Х — MX)'d = d’d, (22)

Нам нужно найти максимум (21) no d, сохраняя (22) по­стоянным. Если — множитель Лагранжа, то задача сво­дится к нахождению максимума выражения

. (23) -

Приравнивая нулю производные (23) по компонентам вектора d, получим

. (24)

Так как (-)’d — скаляр, скажем v, то (24) можно записать в виде

-=. (25)

Поэтому вектор d, являющийся решением уравнения (24), пропорционален вектору .

В заключение отметим, что если мы имеем выборку объема N либо из , либо из₂ , то можно использовать выборочное среднее значение и классифицировать выборку как выборку изили из.

1означает, что р₂(х) = 0,